
02_Молекулярная_физика
.pdf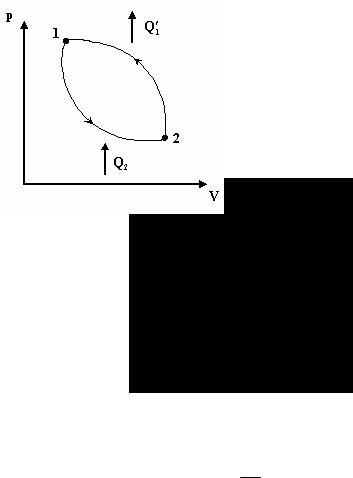
51
Q2 = −Q2 - количество теплоты, отданное за цикл рабочим телом холодильнику.
Холодильная машина
Рассмотрим следующий цикл. Рабочее тело получает количество теплоты Q2 и отдает те6лу с более высокой температурой количество теплоты
Q1′ .
Такое устройство называется холодильной машиной и характеризуется холодильным коэффициентом, равным
ε = QA2′ ,
где A′ - работа, совершаемая внешними силами над рабочим телом.
A′ = |
|
Q1′ |
|
−Q2 , ε = |
|
Q2 |
. |
||
|
|
||||||||
|
|
|
′ |
|
−Q2 |
||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
|
|
Q1 |
|
|
|
Второе начало термодинамики
Наличие холодильника в тепловой машине означает, что не все тепло Q1 , которое нагреватель передает рабочему телу, превращается в работу. Возникает мысль о машине без холодильника, в которой вся тепловая энергия используется для совершения механической работы. Сконструировать такую машину пытались многие, но оказалось, что это сделать невозможно. Это утверждение называется вторым началом термодинамики.
Невозможно устройство, работающее циклически и превращающее все подводимое к нему тепло в механическую работу.
Цикл Карно
Если невозможна машина, полностью превращающая тепло в работу, то остается придумать такую, которая бы делала это наиболее эффективно, т.е. с максимальным КПД. Такую задачу решил Карно, предложив процесс, получивший название цикла Карно.
52
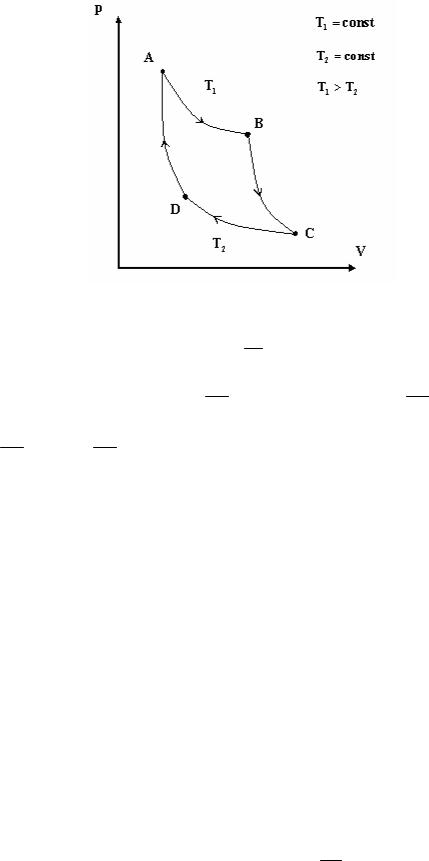
Цикл Карно состоит из двух изотерм AB и CD и двух адиабат BC и DA. Изотерма AB характеризуется температурой T1 , а изотерма CD температурой
T2 , причем T1 > T2 .
Найдем КПД цикла
A = AAB + ABC + ACD + ADA
V V = νRT1ln VB − νRT2 ln VC ,
A D
Для B и C: T1VBγ−1 = T2VCγ−1 . Для A и D: T1VAγ−1 = T2VDγ−1 .
Делим и логарифмируем:
Следовательно:
η = A ,
Q1
= νRT1ln VB + νCV (T1 −T2 )+ νRT2 ln VD + νCV (T2 −T1 )= VA VC
|
|
|
|
|
ln |
V |
|
|
|
|
|
VB |
|
T2 |
|
C |
|
|
|
||
|
|
VD |
||||||||
A = νRT1ln |
1− |
|
|
|
|
|
. |
|||
V |
T |
|
|
VB |
|
|
||||
|
|
|
ln |
|
|
|
|
|||
|
A |
|
1 |
|
|
|
|
|
|
|
|
|
|
VA |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
(γ−1)ln |
VB |
= (γ−1)ln |
VC |
|
, |
||||||||||||
|
|
V |
|||||||||||||||
|
|
|
V |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
A |
|
|
|
|
|
|
|
|
D |
|
|||
ln |
VB |
= ln |
VC |
, |
|
VB |
= |
|
VC |
. |
|||||||
V |
|
|
V |
V |
|||||||||||||
|
|
|
|
V |
|
|
|
|
|
|
|
||||||
|
A |
|
|
|
|
D |
|
|
A |
|
|
|
D |
|
|||
|
|
|
|
VB |
|
|
|
T2 |
|
|
|
|
|
( ) |
|||
A = νRT1ln |
|
− |
|
|
|
|
|
|
|||||||||
V |
T |
|
|
|
|
||||||||||||
1 |
|
|
. |
|
|
|
|||||||||||
|
|
|
|
|
A |
|
|
1 |
|
|
|
|
|
|
|||
Далее
QAB = (υB − υA )+ AAB = νRT1ln VB > 0 , VA

|
|
|
53 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
QBC = 0 , |
|
|
|
|
|
|
|
|
||||||||
QCD = (υ0 − υC )+ νRT2ln |
VD |
|
|
= νRT2ln |
VD |
< 0 , |
|||||||||||||
|
V |
V |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
C |
|
|||
|
|
|
QDA = 0 . |
|
|
|
|
|
|
|
|
||||||||
Следовательно, т.к. Q1 > 0 , имеем |
|
|
|
VB |
|
|
|
|
|
|
|
|
|||||||
Q1 = QAB = νRT1ln |
. |
|
( ) |
|
|||||||||||||||
V |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из ( ) и ( ) получим для КПД |
|
|
|
A |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
VB |
|
|
|
T2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
A |
|
νRT1ln V |
T |
|
|
T |
|
|||||||||||
|
|
1− |
|
|
|
|
|
||||||||||||
η = |
|
= |
|
A |
|
1 |
|
=1− |
|
2 |
|
, |
|||||||
Q |
νRT1ln |
|
|
|
|
T |
|||||||||||||
|
|
|
|
VB |
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
V |
|
|
|
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A
η =1− T2 .
T1
Цикл Карно – идеальный цикл, в котором отсутствуют потери тепла. Тепловая машина, работающая по циклу Карно, называется идеальной тепловой машиной.
КПД цикла Карно с идеальным газом не зависит от рода газа и определяется только температурами нагревателя и холодильника.
КПД любой тепловой машины, имеющей нагреватель с температурой T1 и холодильник с температурой T2 не больше чем КПД идеальной тепловой машины, работающей по циклу Карно с теми же нагревателем и холодильником.
В заключение запишем уравнение цикла Карно для давления и объема:
pAVA = pBVB , pBVBγ = pCVCγ ,
pCVC = pDVD , pDVDγ = pAVAγ .
Циклы Отто и Дизеля
Распыленное в воздухе горючее (бензин) подается в цилиндр – линия 0-1. Затем происходит адиабатное сжатие 1-2. В состояние 2 с помощью искры происходит воспаление смеси. Процесс сгорания смеси происходит достаточно быстро, так что процесс 2-3 можно считать изохорным. Затем следует адиабатное расширение 3-4 – это рабочий ход поршня. После изохорного охлаждения 4-1 открывается клапан, и продукты сгорания выталкиваются в атмосферу – линия 1-0. Затем в цилиндр поступает новая порция горючего.

54
КПД цикла Отто равен:
η=1− V2 γ−1 .
V1
Циклы Отто используются с применением качественного горючего – бензина.
В других случаях применяется цикл Дизеля.
На участке 0-1 происходит подача воздуха в цилиндр и затем его адиабатное сжатие 1-2. При этом воздух сильно нагревается. Затем в цилиндр впрыскивается распыленное горючее, которое сгорает так, что процесс можно считать изобарным 2-3. После адиабатного расширения 3-4 (рабочий ход) происходит изохорное охлаждение 4-1 и выброс продуктов сгорания в атмосферу.

55
ГЛАВА 5. РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА И РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА
Случайные величины. Вероятность
Предположим, что мы измеряем некоторую величину x . Пусть в первом измерении величина x имеет значение x1 , во втором – значение x2 , в третьем -
x3 и т.д.
Если изменение значений носит непредсказуемый характер, то величина x может принимать случайные значения из последовательности
x1,x2 ,...xi...xk .
В таком случае случайная величина x имеет дискретные значения. Пусть Ni - число частиц системы, для которых значение величины x оказалось
равным xi .
Факт, заключающийся в том, что величина x принимает некоторое значение, называется событием.
Можно сказать, что Ni - число событий, в которых величина x имеет значение xi .
Запишем отношение: NNi .
Предел, к которому стремится величина NNi при N → ∞ называется вероятностью того, что величина x имеет значение xi
ω(xi )= lim Ni .
N→∞ N
При достаточно большом N можно считать что
ω(xi )= NNi , ω(xi )≤1.
Кроме случайных событий бывают еще события двух типов: достоверные и недостоверные.
Достоверное событие – это такое событие, которое происходит в любом из экспериментов, независимо от количества экспериментов. Вероятность достоверного события равна единице.
ωд =1 .
Недостоверное событие – это такое событие, которое никогда не происходит ни в одном из экспериментов. Вероятность недостоверного события равна нулю.
ωн = 0 .
56
Функция распределения
Пусть случайная величина x может принимать любое значение из некоторого интервала (x1, x2 ). В таком случае величина x имеет непрерывное распределение значений.
Возьмем элементарный интервал значений (x, x + dx). |
|
|
Обозначим dω(x) - вероятность того, что |
значение x находится в |
|
интервале (x, x + dx ). Часто говорят, что значение |
x попадает |
в интервал |
(x, x + dx). |
|
|
Очевидно, что вероятность зависит от ширины интервала dx |
и от самого |
|
значения x . |
|
|
dω(x)= f (x)dx , ( ) |
|
|
где f (x) - некоторая функция и называется она функцией распределения значений величины x или функцией распределения.
Возьмем единичный интервал значений:
dx =1, dω(x)= dω1(x), f (x)= dω1(x).
Функция распределения численно равна вероятности того, что значение случайной величины x находится в единичном интервале вблизи некоторого значения этой величины.
Функция распределения f (x) называется также плотностью вероятности. Проинтегрируем выражение ( )
x2
∫dω(x)∫f (x)dx .
x1
Обозначим
x 2
∆ω(x)= ∫dω(x).
x1
x 2
∆ω(x)= ∫f (x)dx .
x1
Величина ∆ω(x) есть вероятность того, что значение случайной величины x находится в интервале (x1 , x2 ).
Закон умножения вероятностей.
Величины называются статически независимыми, если значение одной из них не зависит от того, какие значения принимают остальные величины.
|
57 |
|
|
Пусть каждая частица |
характеризуется |
двумя величинами |
x и y , |
являющимися независимыми. Обозначим dω(x) |
и dω(y) - вероятности того, что |
||
x имеет значение в интервале (x,x +dx), а y - в интервале (y,y +dy). |
|
||
Обозначим |
|
|
|
dω(x и y) - вероятность того, |
что величины x |
и y для некоторой |
частицы |
одновременно имеют значения в интервале (x,x +dx) и (y,y +dy). Такая вероятность равна:
dω(x и y)= dω(x) dω(y).
Формула называется законом умножения вероятностей.
Среднее значение величин
Пусть ϕ(x) - функция случайной величины x , имеющей непрерывное распределение значений.
Средним значением случайной величины x называется величина, равная
x2
<x >= ∫xdω(x),
x1
x2
<x >= ∫xf (x)dx ,
x1
где (x1,x2 ) - интервал изменения x .
Средним значением функции случайной величины ϕ(x) называется величина, равная
x2
<ϕ(x)>= ∫ϕ(x)dω(x),
x1
x2
<ϕ(x)>= ∫ϕ(x)f (x)dx .
x1
Распределение частиц системы
Запишем
dω(x)= f (x)dx .
Умножим на число частиц системы N обе части
Ndω(x)= Nf (x)dx .
58
Обозначим
dN = Ndω(x).
|
Величина dN есть число частиц, |
имеющих значение величины x в |
||||||
интервале (x,x +dx) |
|
|
|
|||||
|
|
|
dN = Nf (x)dx . |
( ) |
||||
|
Пусть интервал изменения величины x |
равен (x1,x2 ). |
||||||
|
Проинтегрируем ( ) |
|
|
|
||||
|
|
|
x 2 |
|
|
x 2 |
||
|
|
|
∫dN = ∫Nf (x)dx = N ∫f (x)dx , |
|||||
|
|
|
x1 |
|
|
x1 |
||
|
|
|
|
|
x 2 |
|
|
|
|
|
|
∆N = N ∫f (x)dx . |
|||||
|
|
|
|
|
x1 |
|
|
|
∆N есть число частиц, имеющих значение величины x в интервале (x1,x2 ). |
||||||||
Запишем |
|
|
|
|
|
|||
|
|
|
|
∆N |
x |
|
|
|
|
|
|
|
= ∫2 f (x)dx , |
||||
|
|
|
|
N |
||||
|
|
|
|
x1 |
|
|
||
|
|
|
|
|
|
|
||
где |
∆N |
|
- относительное число частиц, |
для которых значение x попадает в |
||||
N |
||||||||
|
(x1 , x2 ). |
|
|
|
||||
интервал |
|
|
|
|||||
Распределение проекции скорости молекулы
Три декартовые проекции скорости молекул являются статически независимыми случайными величинами.
Поскольку, направления x, y,z в пространстве равноценны, то величины υx ,υy ,υz должны иметь одинаковую функцию распределения, поэтому
достаточно найти, например, функцию распределения f (Vx ). Две другие функции f (Vy ), f (Vz ) будут иметь такой же вид, что и f (Vx ).
В математике существует множество функций распределения. Однако в реальной жизни чаще всего встречается нормальное распределение:
f (x)= |
1 |
|
|
x |
2 |
|
, |
|
|
|
|
||||
τ 2π |
exp |
− |
2τ2 |
|
|||
где τ- параметр распределения.
Дж.Максвелл предполагал, что распределение проекции скорости молекулы также является нормальным, и определил для него параметр τ,
τ = kT ,  m0
m0

59
m0 - масса молекулы,
T - температура. Для υx :
|
m0 |
|
1 |
|
|
2 |
|
||||
|
|
|
|||
f (υx )= |
|
|
|
− |
|
|
|
exp |
|||
|
2π kT |
|
|
|
|
m0υ2x .
2kT
Аналогичное распределение для υy ,υz . Две кривые соответствуют двум
значениям температуры
T1 < T2 .
С ростом температуры кривая f (Vx ) расширяется и сжимается.
Из условия нормировки:
+∞
∫f (υx )dυx =1.
−∞
Площадь, ограниченная каждой кривой равна 1.
Зная функцию f (Vx ) можно получить определенную информацию о системе.
Пусть (υx1 , υx2 ) некоторый интервал значений проекции скорости υx . Найдем
вероятность того, что значение проекции скорости молекулы υx принадлежит этому интервалу (υx1 ,υx2 ).
υx2 |
|
|
|
m0 |
|
|
1 |
|
υx2 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
m0υx |
|
||||||
∆ω(υx )= ∫f (x)dVx = |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
∫ exp − |
|
2kT |
dυx . |
||||||||
υx1 |
|
|
2π kT |
|
|
υx1 |
|
|
|
|
||||||
Определим число молекул ∆N , проекции, скорости которых υx также |
||||||||||||||||
имеют значения в интервале (υx1 ,υx2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υx2 |
|
|
m0 |
|
|
1 |
υx2 |
|
|
|
2 |
|||||
|
|
2 |
|
|
||||||||||||
∆N(υx )= N ∫f (x)dυx = |
|
|
∫ |
|
− |
m0υx |
|
|||||||||
|
|
|
|
|
||||||||||||
2πkT |
|
exp |
2kT |
|
dυx . |
|||||||||||
υx1 |
|
|
|
|
υx1 |
|
|
|
|
|
||||||
Найдем среднее значение проекции скорости на ось x .

60
υx2 |
+∞ |
|
m0 |
|
1 |
+∞ |
|
|
2 |
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
m0υx |
|
|
||
< υx >= ∫ |
υxf (υx )dυx = ∫υxf (υx )dυx = |
|
|
∫ |
− |
|
( ) |
||||
|
|
|
υxexp |
2kT |
dυx . |
||||||
υx1 |
−∞ |
|
2πkT |
|
−∞ |
|
|
|
|
||
Интеграл ( ) оказывается равным нулю, следовательно |
|
|
|||||||||
< υx >= 0 .
Очевидно, что
< υy >= 0 , < υz >= 0 .
Распределение модуля скорости молекул
Обозначим
dω(υ) - вероятность того, что модуль скорости молекулы имеет значение в интервале: (υ, υ+dυ).
Очевидно, что
dω(υ)= f (υ)dυ,
где f (υ) - функция распределения модуля скорости. Наша задача – найти выражение для f (υ).
Возьмем три взаимноперпендикулярные оси υx ,υy ,υz , на которых откладываем значения проекций скорости молекулы υx ,υy ,υz . От определения пространство скоростей или υ- пространство.
