Метод Гаусса с выбором главного элемента

В данном случае помимо соблюдения условия a_kk  0 при реализации формул (1.2—1.4) необходимо, чтобы ведущий (главный) элемент в текущем столбце в процессе преобразований исходной матрицы имел максимальное по модулю значение. Это также достигается перестановкой строк матрицы.

Блок-схема модифицированного метода Гаусса представлена на рисунке 1.1.

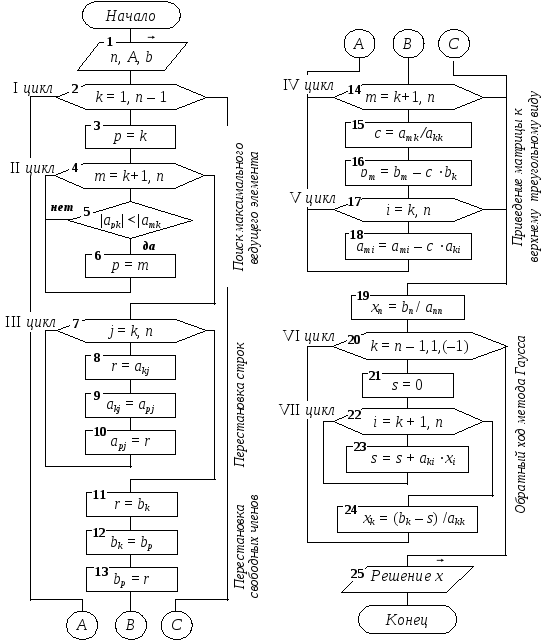
Рисунок 1.1 — Блок-схема модифицированного метода Гаусса

Проведем анализ предложенной схемы на примере системы n = 3 ( = 0,001).

; .

(*)

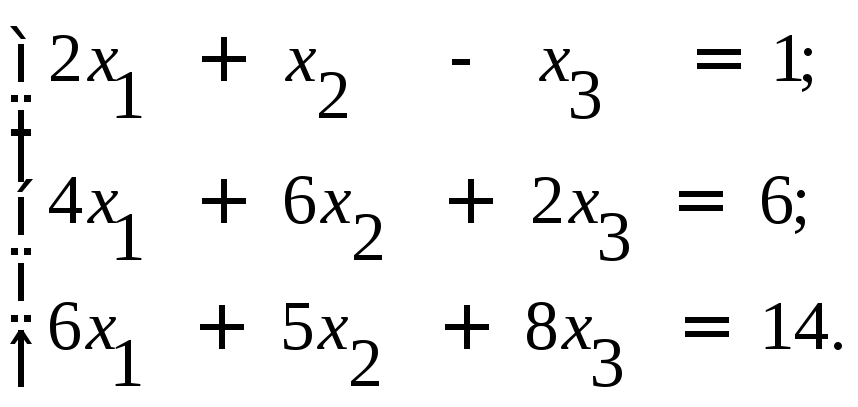
Блок 1. Ввод исходных данных: n — порядок системы, A — матрица коэффициентов при неизвестных, b — вектор свободных членов.

Блок 2. I цикл прямого хода (для k, изменяющегося от 1 до предпоследнего значения, т. е. до n – 1) обеспечивает исключение из главной диагонали матрицы А элемента a_kk = 0 благодаря поиску максимального элемента a_kk в текущем столбце, осуществляемому в блоках 3  6 с помощью II цикла.

Далее, с помощью III цикла, в блоках 7  13 выполняется перестановка текущей строки и строки с максимальным элементом в k-м столбце (ее номер р).

Затем реализуются расчеты по формулам (1.3) прямого хода Гаусса в блоках IV и V циклов.

Проведем поблочный анализ в среде рассмотренных I  V циклов на примере.

Блок 3: .

Вход во II цикл.

Блок 4: доn = 3.

Блок 5: < . из (*)

Блок 6: .

Блок 4: .

Блок 5: <. из (*)

Блок 6: .

Выход из II цикла и вход в III цикл блоки 7  10 выполняют перестановку строк матрицы А поэлементно:

Блок 7: (j от 1 до 3).

Блок 8: r = = 2. из (*)

Блок 9: .

Блок 10: .

Блок 7: .

Блок 8: .

Блок 9: .

Блок 10: .

Блок 7 и по аналогии

Выход из III цикла и вход в Блок 11 и далее 12  13 выполняют аналогичную перестановку значений свободных членов:

Вход в IV цикл с измененной системой

;

(**)

для пересчета b₂ вектора

до n = 3,

, из (**)

. из (**)

Вход во вложенный V цикл для пересчета второй строки:

(i от 1 до 3);

.

Выход из V цикла и вход в IV цикл:

Вход в Блок 16:

Выход из IV цикла и вход в V цикл в Блок 17:

(i от 1 до 3);

Выход из V цикла с преобразованной системой

; (***)

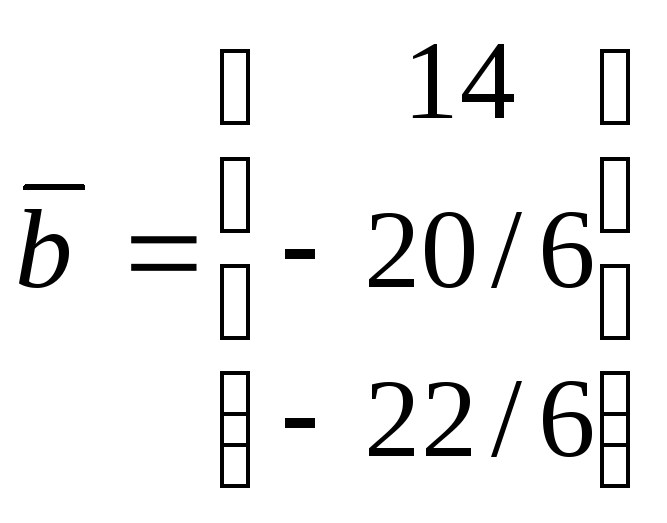и вход по линии А в I цикл:

Вход в Блок 5:

. из (***)

Выход из II цикла и вход в III цикл:

(j от 2 до 3);

из (***)

из (***)

В данном случае на диагонали оказался максимальный элемент, поэтому перестановка 2-й и 3-й строк не выполняется.

Выход из III цикла и вход в I цикл в Блок 11:

Свободный член b₂ остается на своем месте.

Вход в IV цикл:

из (***)

. из (***)

Выход из IV цикла и вход в V цикл:

(i от 2 до 3);

Выход из V цикла и выход из I цикла.

Обратный ход метода Гаусса

В Блоках 1924 реализуются формулы (1.4).

В Блоке 19 из последнего уравнения находится значение x_n (n = 3)

Вход в VI цикл (Блок 20), в котором значение переменной цикла k изменяется от n–1 до 1 с шагом (–1):

Блок 21: .

Вход в VII цикл (Блок 22):

Выход из VII цикла на Блок 24 в VI цикл:

Далее по аналогии:

Выход из VII последнего цикла.

В Блоке 25 (цикл опущен) выполняется вывод на экран полученного решения СЛАУ — вектора , т. е.x_i, i = 1, ..., n. В нашем случае (1; 0; 1).
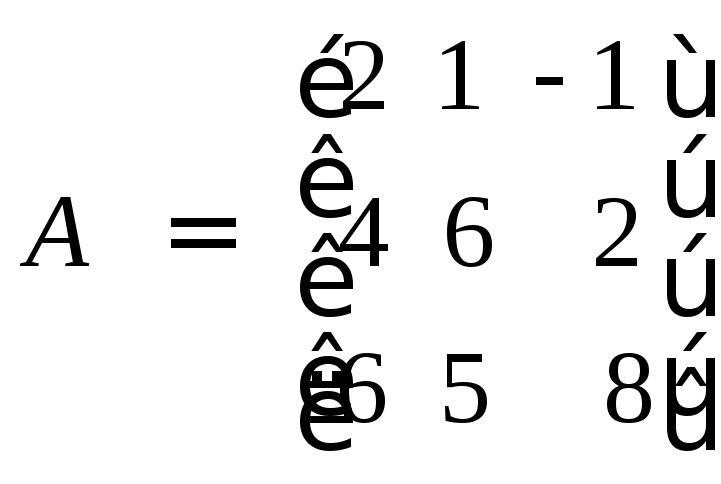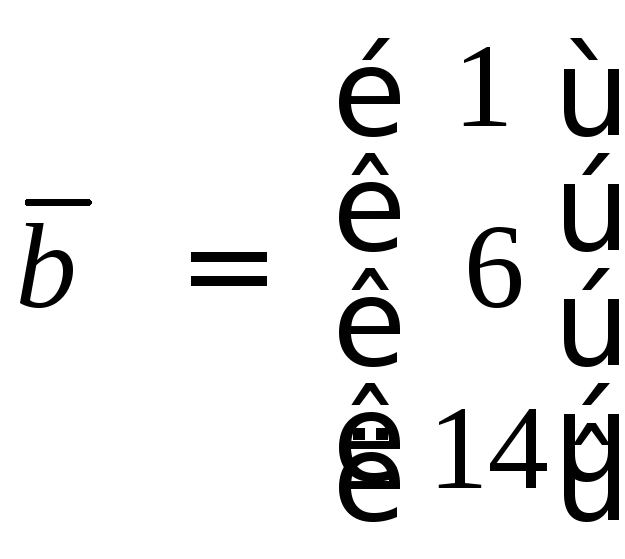
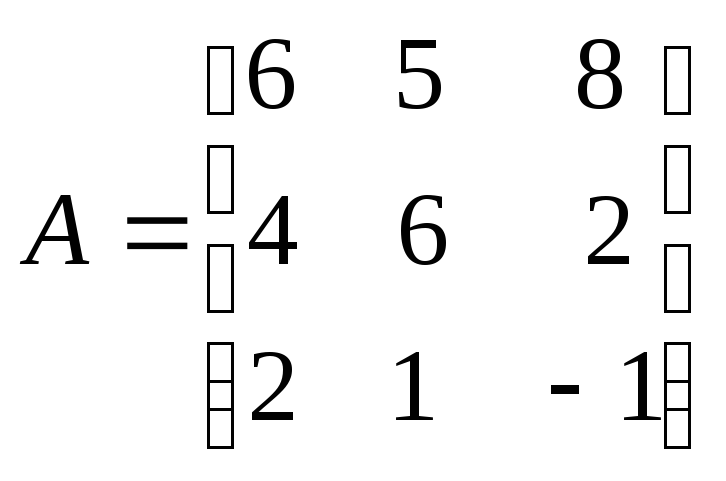