Теорія ймовірностей Заоч. 2010

Цей розподіл використовують в задачах статистичного контролю якості, в теорії надійності, теорії масового обслуговування, для обчислення: кількості вимог на виплату страхових сум за рік,

4. Рівномірний розподіл

Означення 1. НВВ X розподілена рівномірно на проміжку (a,b) , якщо усі її можливі значення належать цьому проміжку і щільність її ймовірностей на цьому проміжку стала, тобто

Величина сталої С визначається умовою нормування

P(a < X < b) = C(b − a) =1.

Цей розподіл задовольняють, наприклад, похибки округлення різноманітних розрахунків.

Числовими характеристиками НВВ X, що розподілена за рівномірним законом, будуть

5. Експоненціальний розподіл

Означення 2. Випадкову величину X називають розподіленою за експоненціальним законом, якщо щільність її ймовірностей має вигляд

де λ > 0 - параметр.

Експоненціальному розподілу задовольняють: час телефонної розмови, час ремонту техніки, час безвідмовної роботи комп'ютера.

50

Числовими характеристиками експоненціального розподілу будуть

6. Нормальний розподіл

Означення 3. Випадкову величину X називають розподіленою нормально, якщо щільність її ймовірностей має вигляд

кривою Гауса.

Для цього розподілу:

M (X ) = a , D(X ) =σ 2 .

Отже, математичне сподівання нормального розподілу дорівнює параметру а цього розподілу, а середнє квадратичне відхилення дорівнює параметру σ .

Зауваження. Якщо випадкова величина Х розподілена за нормальним законом з параметрами а та σ , то випадкова величина

Z = Xσ− a буде розподілена за нормованим нормальним законом і

величини, тобто їх математичне сподівання дорівнює нулю, середнє квадратичне відхилення дорівнює одиниці і кожна з них розподілена за нормальним законом. Тоді сума квадратів цих величин

n

χ2 = ∑Xi2 i =1

51

розподілена за законом χ2 з k = n степенями вільності.

Якщо величини Xi зв'язані одним лінійним співвідношенням,

n

наприклад, ∑Xi = nX , то число ступенів свободи буде k = n −1.

i =1

Зауважимо, що розподіл χ2 визначається параметром – числом ступенів свободи k . Коли k зростає, розподіл χ2 прямує до нормального розподілу дуже повільно.

8. Розподіл Стьюдента

Нехай X - нормальна нормована випадкова величина, а Y - незалежна від X величина, яка розподілена за законом хі-квадрат з k степенями свободи. Тоді величина

T = XY

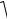k

має розподіл, який називають t розподілом або розподілом Стьюдента (це є псевдонім англійського статистика Вільяма Госсета) з k степенями вільності.

При зростанні k розподіл Стьюдента швидко наближується до нормального розподілу.

Питання для самоконтролю

1.Визначення нормального закону розподілу.

2.Як впливають параметри a, σ на графіки функцій f(x), F(x) загального нормального закону.

3.Що називають нормованим нормальним законом?

4.Чому дорівнює Мо і Ме для нормального закону розподілу?

5.Навести визначення μ3 для нормального розподілу.

Література

Обов’язкова: [1]. Додаткова:[1], [4], [7].

52

Тема 6. Багатовимірні випадкові величини Мета роботи: вивчити поняття двовимірної випадкової

величини, її числові характеристики, закони розподілу.

План вивчення теми

1.Система двох дискретних випадкових величин (Х, Y) та їх числові характеристики.

2.Коефіцієнт кореляції.

3.Умовні закони розподілу.

4.Функція розподілу ймовірностей системи двох випадкових величин.

5.Щільність ймовірностей системи двох випадкових величин.

6.Числові характеристики системи двох неперервних випадкових величин.

Методичні рекомендації до самостійної роботи

На одному й тому самому просторі елементарних подій Ω можна визначити не одну, а кілька випадкових величин. В цьому разі кажуть, що визначена багатовимірна випадкова величина.

Означення. Одночасна поява внаслідок експерименту n випадкових величин (X1, X 2 ,..., X n ) з певною ймовірністю являє собою n-вимірну випадкову величину, яку називають також

системою n випадкових величин, або випадковим вектором.

1. Система двох дискретних випадкових величин (Х, Y) та їх числові характеристики

Законом розподілу двох дискретних випадкових величин називають перелік можливих значень Y = yi , X = x j та відповідних

їм ймовірностей спільної появи.

У табличній формі цей закон має вигляд:

53

Тут:

σ(Y ) =σ y = D(Y ) .

54

2. Коефіцієнт кореляції

Під час вивчення системи двох і більше випадкових величин доводиться з’ясовувати наявність зв’язку між цими величинами та його характер. Для цього застосовують кореляційний момент:

k m

Kxy = M (XY ) − M (X )M (Y ) = ∑∑yi x j pij − M (X )M (Y ) .

i =1 j =1

У разі Kxy = 0 кореляційний зв’язок відсутній.

Тісноту кореляційного зв’язку характеризує коефіцієнт кореляції:

55

Властивості F(x, y):

1. 0 ≤ F(x, y) ≤1.

(a < X < b; c < Y < d) обчислюється за формулою:

P(a < X < b; c < Y < d) = F(b, d ) + F(a, c) − F(a, d) − F(b, c).

5. Щільність ймовірностей системи двох випадкових величин

Ймовірність розміщення системи (X ,Y ) у прямокутній області

Означення. Щільністю ймовірностей системи двох випадкових величин називається друга похідна від функції F(x, y) :

Властивості f (x, y) :

1.f (x, y) ≥ 0, оскільки F(x, y) є неспадною функцією аргументів x і

y .

2.Умова нормування системи двох неперервних випадкових величин

∞ ∞

(X ,Y ) є: ∫ ∫ f (x, y)dx dy =1.

−∞ −∞

3. Функція розподілу ймовірностей системи двох неперервних випадкових величин визначається з рівняння:

x y

F(x, y) = ∫ ∫ f (x, y)dx dy .

−∞ −∞

56

6. Числові характеристики системи двох неперервних випадкових величин

∞ ∞

M ( X ) = ∫ ∫xf (x, y)dx dy ,

−∞ −∞

∞ ∞

D(X ) = ∫ ∫x2 f (x, y)dx dy − M 2 ( X ) ,

−∞ −∞

∞ ∞

M (Y ) = ∫ ∫yf (x, y)dx dy ,

−∞ −∞

∞ ∞

D(Y ) = ∫ ∫y2 f (x, y)dx dy − M 2 (Y ) ,

−∞ −∞

∞ ∞

Kxy = ∫ ∫xyf (x, y)dx dy − M (X )M (Y ).

−∞ −∞

Питання для самоконтролю

1.Означення багатовимірної випадкової величини .

2.Означення закону розподілу багатовимірної випадкової величини.

3.Основні числові характеристики для системи двох дискретних випадкових величин.

4.Що визначає кореляційний момент ?

5.Чому дорівнюєK xy ?

6.Коефіцієнт кореляції та його властивості.

7.ЯкщоK xy =0 , то чому дорівнює rxy ?

8.Що називається умовним законом розподілу Y/x ?

9. Умови нормування для системи двох ДВВ.

Література

Обов’язкова: [1]. Додаткова:[1], [4], [7].

57

Тема 7. Функції випадкового аргументу Мета роботи: вивчити поняття функції, закону розподілу та

числові характеристики для функції дискретного і неперервного випадкового аргументу.

План вивчення теми

1.Поняття функції.

2.Закон розподілу та числові характеристики функції. дискретного випадкового аргументу.

3.Закон розподілу та числові характеристики функції. неперервного випадкового аргументу.

Методичні рекомендації до самостійної роботи

1.Поняття функції

Убагатьох випадках треба розглядати дві випадкові величини X та Y. Так, наприклад, при аналізі діяльності підприємства треба враховувати кількість усіх працюючих X та кількість зроблених виробів Y. З різних причин кількість працюючих та зроблених виробів кожного дня можуть бути різними, тобто X та Y будуть випадковими величинами.

Означення. Якщо вказано закон, за яким кожному можливому значенню випадкової величини X відповідає певне значення випадкової величини Y, то Y називають функцією X і позначають

Y =ϕ(X ) .

Відзначимо, що іноді різним можливим значенням випадкової величини X відповідають однакові значення Y. Наприклад, якщо Y = X2, то значенням 3 та –3 випадкової величини X відповідає одне значення випадкової величини Y = 9.

Однією із можливих задач теорії ймовірностей є визначення законів розподілу та числових характеристик функцій випадкового аргументу, закон розподілу якого відомий. Вкажемо основні формули для розв'язування цієї задачі.

58

2. Закон розподілу та числові характеристики функції дискретного випадкового аргументу

Нехай Y =ϕ(X ) , аргумент X - дискретна випадкова величина. У цьому випадку Y також дискретна випадкова величина із відповідними значеннями.

Математичне сподівання, дисперсію та середнє квадратичне відхилення функції Y обчислюють за формулами:

3. Закон розподілу та числові характеристики функції неперервного випадкового аргументу

Нехай X — неперервна випадкова величина, закон розподілу якої заданий диференціальною функцією розподілу (щільністю ймовірностей) f (x); випадкова величина Y =ϕ(X ) .

Якщо ϕ - диференційовна функція, монотонна на усьому проміжку можливих значень X, то щільність розподілу функції

Y =ϕ(X ) визначають так

g( y) = f (ψ ( y)) ψ′( y) .

де ψ - функція, обернена по відношенню до функції ϕ .

Питання для самоконтролю

1. Як обчислити щільність ймовірностей випадкової величини Y , якщо Y =α(X ) , де α(X ) — монотонна функція, і відомий

59