
Теорія ймовірностей Заоч. 2010
.pdf
Знайти DВ, σв.
а) DВ=1, σв=1; б) DВ=4, σв=2; в) DВ=1, σв=-1; г) DВ=12, σв=3.
3.Знайти емпіричну функцію розподілу за даним розподілом вибірки:
4.Знайти мінімальний об'єм вибірки, при якому з надійністю γ=0,99 точність оцінки математичного сподівання нормально розподіленої генеральної сукупності буде дорівнювати 0,2. Відомо, що σГ=1,5.
а) n=179; б) n=216; в) n=298; г) n=380.
5.Знайти довірчий інтервал з надійністю 0,95 для оцінки невідомого математичного сподівання а нормально розподіленої випадкової
величини Х, якщо σ2=16, xB =15, n=25.
а) (1,4; 1,5); б) (3,63; 3,77); в) (-14,2; -13,7); г) (13,43; 16,57).
Тема 12. Перевірка статистичних гіпотез
1. Що називається рівнем значущості? а) імовірність здійснити похибку I роду; б) імовірність здійснити похибку ΙΙ роду;
в) імовірність, з якою буде прийнято вірне рішення; г) немає правильної відповіді.
2. Контрольна довжина деякої деталі має становити а=12мм. Контрольні вимірювання 25 випадково відібраних деталей дали такі результати:
Довжина, мм |
11 |
11,5 |
12 |
12,5 |
13 |
|
|
|
|
|
|
Кіл-ть деталей |
6 |
8 |
7 |
3 |
1 |
|
|
|
|
|
|
При рівні значущості 0,01 перевірити основну гіпотезу H0 : a = 12 при
140
конкуруючий гіпотезі Hα : a > 345 :
1)знайти спостережуване значення критерію;
2)знайти критичне значення критерію;
3)H0 приймаємо; б) H0 відхиляємо.
3. Використовуючи критерій Пірсона (χ-квадрат) з рівнем значущості α=0,05, перевірити гіпотезу про нормальний розподіл генеральної
сукупності X, якщо відомі емпіричні nk |
та теоретичні nk′ частоти. |
||||||||
|
|
|
|
|
|
|
|
|
|
nk |
8 |
16 |
40 |
72 |
36 |
18 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
nk′ |
6 |
18 |
36 |
76 |
39 |
18 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
1)знайти спостережуване значення критерію;
2)знайти критичне значення критерію;
а) χkp2 =9,5, Н0 відхиляємо; б) χkp2 =9,5, Н0 приймаємо; в) χkp2 =3,06, Н0 приймаємо; г) χkp2 =3,06, Н0 відхиляємо.
Теми 13, 15. Елементи теорії регресії. Елементи теорії кореляції
1. Як статистична оцінка β0* впливає на зміщення лінії регресії?
а) викликає вертикальне зміщення; б) викликає горизонтальне зміщення; в) викликає зміну кута нахилу; г) жодним чином не впливає.
2. Залежність собівартості від вирощеного врожаю соняшнику наведено в таблиці:
Y=уі, |
10,36 |
11,56 |
13,29 |
14,51 |
15,6 |
14,25 |
17,36 |
16,23 |
|
грн/ц. |
|||||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
X=хі, ц/га |
1,23 |
1,33 |
1,43 |
1,53 |
1,63 |
1,73 |
1,83 |
1,93 |
|
|
|
|
|
|
|
|
|
|
1)визначити β1* : а) –2,13; б) 8,78; в) 7; г) 20,8.
2)визначити β0* : а) 0,27; 6) 0,56; в) –0,39; г) 7,65.
3)обчислити КXY: а) 0,52; б) 1,05; в) 60,12; г) 0,46.
141
4) знайти коефіцієнт кореляції: а) 0,14; б) 1,05; в) 0,22; г) 0,77.
Тема 13. Елементи дисперсійного аналізу
1.Що таке рівень впливу певного фактора на досліджувану ознаку Х?
2.Досліджується залежність урожайності пшениці від внесення в грунт добрив. Результати досліджень наведені в таблиці:
Ступінь впливу фактора А (тип |
Урожайність, |
|
добрива) |
ц/га |
|
А1 |
90; 85; 105; 110; |
|
95 |
||
|
||
А2 |
80; 110; 115; 90; |
|
105 |
||
|
||
А3 |
75; 120; 110; 90; |
|
85 |
||
|
При рівні значущості α=0,01 з’ясувати вплив типу добрива на врожайність пшениці.
1)Знайти загальну середню: а) 119,73; б) 110; в) 130,2; г) 122,08;
2)обчислити міжгрупову дисперсію: а) 39,1; б) 47,1; в) 54,17; г) 52,3;
3)знайти спостережуване значення критерію: а) 5,096; б) 1,02; в) 10,4; г) 12,3;
4)знайти критичне значення критерію: а) вплив є істотним; б) вплив несуттєвий.
142
5. МЕТОДИЧНІ РЕКОМЕНДАЦІЇ І ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ КОНТРОЛЬНОЇ РОБОТИ
Згідно з учбовим планом з модуля 2 «Теорія ймовірностей та математичної статистики» студенти виконують індивідуальне завдання, яке охоплює всі теми.
Метою виконання індивідуального завдання є перевірка знань і навичок, необхідних для виконання завдань по темах: основні поняття і основні формули теорії ймовірностей; спроби за схемою Бернуллі; повторні незалежні випробування; випадкові величини; функція розподілу ймовірностей; числові характеристики випадкових величин. Основні закони розподілу; багатовимірні випадкові величини; закон великих чисел. Граничні теореми; вибірковий метод; статистичні оцінки параметрів розподілу; статистична перевірка статистичних гіпотез; елементи дисперсійного аналізу; елементи теорії кореляції; елементи регресійного аналізу. Елементи теорії випадкових процесів.
Індивідуальне завдання виконується після вивчення теоретичного матеріалу та опанування рекомендованої літератури.
Індивідуальне завдання складається з 17 варіантів. Варіанти рівноцінні за об’ємом і ступенем складності.
Методичні вказівки до виконання завдань
Вибір відповідного варіанту здійснюється студентом послідовно за номером журналу. Номеру варіанта відповідають номери задач по темам.
Наприклад: варіант № 1, задачі 1.1, 2.1, 3.1, 4.1, 5.1, 6.1.... Перед виконанням завдань необхідно переглянути типові приклади розв’язку поданих задач.
143
Приклади розв’язування завдань
Завдання № 1
Випадкові події А1, А2, А3, А4 є попарно несумісними і утворюють
повну групу. |
Знайти |
Р(А1), |
Р(А2), |
|
Р(А3), Р(А4), |
коли |
відомо, що |
|||
Р(А1)=0,2Р(А2), Р(А2)=0,8Р(А3), Р(А3)=0,5Р(А4). |
|
|
|
|||||||
Розв’язання. Оскільки випадкові події А1, А2, |
А3, А4 є попарно |
|||||||||
|
|
|
|
|
|
|
|
n |
|
=1дістанемо: |
несумісними і утворюють повну групу, то згідно з P U Ai |
|
|||||||||
|
|
|
|
|
|
|
i =1 |
|
|
|
|
4 |
|
=Р(А )+Р(А )+Р(А )+Р(А )=1 |
|
|
|
||||
P U A |
|
|
|
|||||||
|
|
i |
|
1 |
2 |
3 |
4 |
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
За умовою задачі знаходимо:
Р(А2)=0,8Р(А3)=0,8·0,5Р(А4)=0,4Р(А4); Р(А1)=0,2Р(А2)=0,2·0,4Р(А4)=0,08Р(А4); Отже, 0,08Р(А4)+0,4Р(А4)+0,5Р(А4)+Р(А4)=1; Р(А4)=1/(0,08+0,4+0,5+1)=1/1,98=100/198; Р(А3)=0,5Р(А4)=(0,5·100)/198=50/198; Р(А2)=0,4Р(А4)=(0,4·100)/198=40/198; Р(А1)=0,08Р(А4)=(0,08·100)/198=8/198.
Завдання № 2
З урни, яка містить три білих та сім чорних куль беруть навмання послідовно дві кулі. Відомо, що перша куля біла (подія В). Яка ймовірність того, що друга куля також виявиться білою?
144

Розв’язання. Після здійснення першого випробування в урні залишилося дві білі та сім чорних куль. Шукана ймовірність, на підставі
класичного означення ймовірності, дорівнює: P(A/B)= |
|
. |
|
|
|
Для знаходження P(A/B) скористаємося означенням умовної ймовірності. Ймовірність появи білої кулі при першому випробуванні
P(B)=
Знайдемо ймовірність |
|
того, що при першому й другому |
|
|
|
випробуванні з’явилися білі кулі.
Знайдемо загальну кількість елементарних подій:
n = A102 =10 9 = 90;
Знайдемо кількість елементарних подій у яких складається подія
A ∩B:
m = A32 = 3 2 = 6.
Тому =
145

Отже P(A/B) =
Завдання № 3
Перша фабрика виробила 3000 приладів, друга - 10000, третя - 1000 приладів. Перша фабрика випускає в середньому 1% бракованих приладів, друга - 05%, третя - 1,5%. Прилад вибраний навмання, виявився бракованим. Яка ймовірність того, що цей прилад виробила друга фабрика?
Розв’язання. Нехай подія В полягає у тому, що вибраний прилад бракований, подія Ні - у тому, що прилад вироблено на іншій фабриці, і=1, 2, 3. За умовою задачі потрібно знайти P(H2/B). Події Ні (і=1, 2, 3) попарно незалежні. Вони утворюють повну групу подій.
За формулою Байєса:
P(H2 |
/ B)= |
|
|
|
|
|
|
|
|
P(B / H2 )P(H2 ) |
|
|
|
|
|
; |
||||||
|
P(B / H1 )P(H1 )+ P(B / H2 )P(H2 ) |
+ P(B / H3 )P(H3 ) |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||
P(H2 )= |
10 |
;P(H3 )= |
|
1 |
P(H1 )= |
3000 |
|
|
= |
3 |
. |
|
||||||||||
|
14 |
3000 +10000 + |
1000 |
14 |
|
|||||||||||||||||
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
P(B / H1 )= 0,01;P(B / H2 )= 0,005;P(B / H3 )= 0,015; |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
0,005 |
|
|
|
|
|
|
10 |
|
|
|
|
||||
P(H2 |
/ B)= |
|
|
|
|
|
14 |
|
|
= |
≈ 0,53. |
|
|
|
||||||||
3 |
|
|
|
|
|
|
|
1 |
19 |
|
|
|
||||||||||
|
|
|
|
10 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0,01 |
|
|
+ 0,05 |
|
+ 0,015 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
14 |
4 |
14 |
|
|
|
|
|
|
|
|||||||||
Завдання №4
Поданий закон розподілу випадкової величини. Знайти її:
1)математичне сподівання;
2)дисперсію;
146

3) середнє квадратичне відхилення;
X |
2 |
4 |
7 |
9 |
|
|
|
|
|
P |
0,1 |
0,3 |
0,4 |
0,2 |
|
|
|
|
|
Розв’язання. M(Х) = 2·0,1+4·0,3+7·0,4+9·0,2=0,2+1,2+2,8+1,8=6; D(X2) = M(X2) - [M(X)]2;
M(X2) = 4·0,1 + 16·0,3 + 49·0,4+81·0,2 = 0,4 + 4,8 + 19,6 + 16,2 = 41;
D(X)= |
|
σ = D(X ) = 5 = 2,24. |
|
|
|
Завдання №5
Неперервна випадкова величина X подана інтегральною функцією розподілу
|
|
|
а=1; b =8; c=3; d=7. |
|
|
|
|
0, |
x ≤1 |
||
|
|
1 |
|
F(x) = |
|
(x −1), 1 < x ≤ 8 . |
|
|
7 |
||
|
1 |
x > 8 |
|
|
|
||
Знайти:
1.Диференціальну функцію f(x);
2.Побудувати графіки функцій F(x) і f(x);
3.Математичне сподівання Х;
4.Ймовірність того, що Х прийме значення, належне до інтервалу (с, d).
Розв’язання. Знайдемо:
147
|
0, |
x ≤1 |
||
1. Диференціальну функцію f(x): |
|
1 |
|
|
f (x) = |
|
|
|
|
7 |
|
|||
|
|
|
||
|
|
0 |
|
|
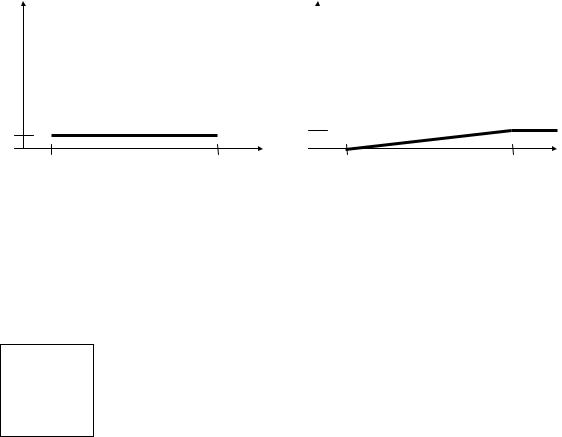
2. Побудуємо графіки функцій F(x) і f(x):
f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(x) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
7 |
1 |
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3. Математичне сподівання Х; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
M (X )= ∫8 |
xf (x)dx = ∫8 |
1 |
xdx = |
1 x2 |
|
18 |
= |
|
x2 |
|
|
18 |
= |
1 |
(64 −1)= |
|
63 |
. |
|||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
7 |
7 |
|
2 |
|
|
14 |
14 |
14 |
||||||||||||||||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 < x ≤8 x >8
8 x
4. Ймовірність того, що Х набуде значення з інтервалу (с, d).
Завдання №6
Задано щільність ймовірностей:
|
|
0, |
|
x ≤ 0; |
|
|
Аsin x, |
|
0 < x ≤π / 2; |
f (x) = |
|
|||
|
|
0, |
|
x >π / 2. |
|
|
|
||
Обчислити А, D(x) , σ(x) . Знайти Мо. |
||||
π / 2 |
−1 |
|
||
|
∫ |
|
|
=1; |
Розв’язання. A = |
|
sin x dx |
||
|
0 |
|
|
|
|
|
|
|
148 |

π / 2 |
π / 2 |
|
M ( X ) = |
∫xf (x)dx = ∫xsin x dx =1. |
|
|
0 |
0 |
|
π / 2 |
π / 2 |
M (X 2 ) = |
∫x2 f (x)dx = ∫x2 sin x dx =π − 2 . |
|
|
0 |
0 |
D(X ) = M (X 2 ) − M 2 (X ) =π −3.
σ(X ) = D( X ) =  π − 3 .
π − 3 .
Функція f (x) набуває максимального значення для x = π2 . Отже, Мо= π2 .
Завдання №7
Випадкова величина Х має нормальний закон розподілу з параметрами а=10, σ = 5 . Знайти симетричний відносно М(Х) інтервал, що містить виміряне значення з ймовірністю р=0,5.
Розв’язання. P(α |
|
|
|
β − a |
α − a |
|
|||||||||
< x < β) = Φ |
σ |
|
− Φ |
σ |
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отже, |
|
|
|
P( |
|
x − a |
|
|
δ |
Тоді |
|
|
|
||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
<δ) = 2Φ |
, |
|
|
|
||||||
δ |
|
р |
|
|
|
|
|
|
σ |
|
|
|
|
|
|
= 0,25 . |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||
Φ |
= |
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|||||
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
За таблицею |
|
для |
функції Φ(x) |
дістанемо: |
δ |
= 0,675, тоді |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
δ =σ 0,675 = 3,4 . |
|
|
|
|
|
|
|
|
|
||||||
Відповідь: |
(10-δ ; 10+δ )=(6,6; 13,4). |
|
|
|
|
|
|||||||||
Завдання №8
Ймовірність появи випадкової події в кожній із 400 незалежних експериментів є величиною сталою і дорівнює 0,9. Використовуючи нерівність Чебишова, оцінити ймовірність події |Х – М(Х)| <ε, якщо ε=10.
149
