Теорія ймовірностей Заоч. 2010

1.Випадковим процесом X=X(t) називають такий процес, коли при будьякому можливому значенні T=ti випадкова функція X=X(tі)

а) є зростаючою; б) є сталою;

в) утворює випадкову величину; г) є детермінованою.

2.Використовуючи нерівність Чебишова, знайти ймовірність того, що випадкова величина Х набуде значення, яке відрізняється від математичного сподівання М( Х ) на величину, що не перевищує потроєного середнього квадратичного відхилення.

а) 0,84; б) 0,97; в) 0,74 г) 0,89.

3.Яке повинна мати значення величина ε у нерівності Чебишова, щоб P( X − a < ε) ≈ 0,879 , коли відомо, що D( Х )=5.

а) 6,42; б) 0,002; в) 2 г) 4,78.

Тема 10, 11. Первинне опрацювання статистичних даних. Статистичне та інтервальне оцінювання параметрів розподілу

1.Якщо математичне сподівання оцінки дорівнює оцінюємому параметру, то оцінка називається:

а) незміщеною; б) правильною; в) ефективною; г) грунтовною.

2.Вибірка задана розподілом частот

Знайти розподіл відносних частот.

130

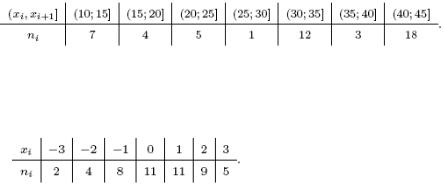
3. Задано інтервальний статистичний розподіл вибірки

Знайти моду. а) 41; б) 56,21; в) 42,34; г) 87,62.

4. Задано статистичний розподіл вибірки

Знайти з надійністю α=0,95 інтервальну оцінку математичного сподівання а нормально розподіленої ознаки Х генеральної сукупності.

а) (4,01; 5); б) (-0,35; 1,23); в) (14,12; 15,07); г) (3,24; 6,51).

5. Знайти мінімальний об'єм вибірки, при якому з надійністю γ=0,95 точність оцінки математичного сподівання нормально розподіленої генеральної сукупності буде дорівнювати 0,2. Відомо, що σГ=1,5.

а) n=179; б) n=216; в) n=298; г) n=380.

Тема 12. Перевірка статистичних гіпотез

1.Для перевірки яких з наведених гіпотез використовується розподіл Стьюдента?

а) гіпотеза про відсутність зв’язку між двома випадковими величинами; б) гіпотеза про закон розподілу випадкової величини; в) гіпотеза про рівність математичного сподівання певному значенню; г) гіпотеза про рівність дисперсії певному значенню.

2.Які гіпотези не є параметричними?

а) гіпотеза про рівність двох дисперсій; б) гіпотеза про закон розподілу випадкової величини;

в) гіпотеза про рівність математичного сподівання певному значенню; г) гіпотеза про рівність дисперсії певному значенню.

3. Щомісячний прибуток на підприємстві у розрахунку на одного робітника Х = хi є випадковою величиною, що має нормальний закон

131

розподілу N (a; 4) . При рівні значущості α = 0,01 перевірити правильність H0 : a = 345 , якщо альтернативна гіпотеза Hα : a < 345 , коли відомо що σГ = 4 і вибіркове середнє для 110 робітників дорівняє xB = 321 .

а) H0 приймаємо; б) H0 відхиляємо.

4. Використовуючи критерій Пірсона (χ-квадрат) з рівнем значущості α=0,01, перевірити гіпотезу про нормальний розподіл генеральної сукупності X, якщо відомі емпіричні nk та теоретичні nk′ частоти.

1)знайти спостережуване значення критерію;

2)знайти критичне значення критерію;

а) викликає вертикальне зміщення; б) викликає горизонтальне зміщення; в) викликає зміну кута нахилу; г) жодним чином не впливає.

2. Залежність вмісту срібла Y в руді від вмісту свинцю X наведено в таблиці:

1)визначити β1* : а) –2,3; б) 0,8; в) 1,7; г) 1,2.

2)визначити β0* : а) 0; 6) 5,6; в) –6,29; г) 8,5.

3)обчислити КXY: а) 13,2; б) 105; в) –6,2; г) 7,5.

4)знайти коефіцієнт кореляції: а) 1; б) 10,5; в) 0,2; г) 0,38.

132

Тема 14. Елементи дисперсійного аналізу

1. Записати математичну модель для двофакторного дисперсійного аналізу.

2. Досліджувався вплив на зносостійкість колінчатих валів технології їх виготовлення – вплив фактора А, який має чотири рівні, т.б. застосовувались чотири технології виготовлення валів. Результати досліджень наведені в таблиці:

При рівні значущості α=0,01 з’ясувати вплив технологій на зносостійкість валів.

1)Знайти загальну середню: а) 9; б) 12,5; в) 11,06; г) 12;

2)обчислити міжгрупову дисперсію: а) 6,17; б) 17; в) 8; г) 24,68;

3)знайти спостережуване значення критерію: а) 2,5; б) 1,02; в) 1,906; г) 1,234;

4)знайти критичне значення критерію: а) вплив істотний; б) вплив несуттєвий.

133

Варіант 4

Теми 1,2. Емпіричні та логічні основи теорії ймовірностей. Основні теореми теорії ймовірностей, їх економічна інтерпретація

1.Яка з подій є більш ймовірною при підкиданні грального кубика: а) поява будь-якого парного числа очок; б) поява 6 очок; в) поява будь-якого числа очок, окрім 1;

г) поява будь-якого числа очок;

2.При підкиданні грального кубіка позначимо А - подія, яка полягає у появі 2 очок, В – парного числа очок. Яке з наступних тверджень невірне?

а) A тягне за собою B; б) B тягне за собою A;

в) Р(В) > P(А); г) АВ = А.

3.Монету кинуто двічі. Зайти імовірність того, що хоча б один раз вона впаде гербом вгору. а) 3/4; б) 1/4; в) 1/2; г) 1.

4.Скільки парних чотиризначних чисел, що складаються з цифр 2, 3, 5, 7 можна одержати, якщо повторення цифр у числах заборонені?

а) немає вірної відповіді; б) 4; в) 6; г) 4!.

5.У крамницю для продажу надійшла продукція з трьох фабрик, відносними частками яких є: 1– 50%; 2 – 30%; 3 – 20%. Брак продукції цих фабрик становить 2%, 3% та 5% відповідно. Знайти імовірність того, що навмання куплений у магазині виріб цих фабрик буде якісним.

а) 0,25; б) 0,63; в) 0,971; г) 1.

134

Тема 3. Схема незалежних випробувань

1.Проводиться n випробувань. Які умови повинні виконуватись, щоб ці випробування утворювали схему Бернуллі?

а) кожне випробування має тільки два наслідки, ймовірність події А в кожному випробуванні однакова, результати випробувань незалежні;

б) кожне випробування має n наслідків, ймовірність події А в кожному випробуванні однакова, результати випробувань незалежні; в) кожне випробування має тільки два наслідки, ймовірність події А в кожному випробуванні однакова; г) кожне випробування має тільки два наслідки.

2.У разі ввімкнення запалювання мотор автомобіля почне працювати з імовірність 0,99. Яка ймовірність того, що мотор почне працювати при 2- х увімкненнях запалювання?

а) 0,9801; б) 0,2303; в) 0,0511; г) 0,9999.

3.Імовірність виготовлення нестандартної деталі дорівнює 0,05. Скільки треба виготовити деталей, щоб найімовірніше число нестандартних деталей було 55? а) 435; б) 1061; в) 1119; г) 1120.

4.Гральний кубик підкидають 800 разів. Яка ймовірність того, що кількість очок, кратна трьом, з’явиться 267 разів?

а) 0,12; б) 0,15; в) 0,05; г) 0,03.

5.Прилад складено з 10 блоків, надійність кожного з яких 0,8. Блоки можуть виходити з ладу незалежно один від одного. Знайти наймовірнішу кількість блоків, що вийдуть з ладу.

а) 0; б) 2; в) 7; г) 3.

135

Тема 4. Випадкові величини та їх економічна інтерпретація

1.Які з наведених нижче випадкових велечин є дискретними: а) число влучень у мішень при десяти незалежних пострілах;

б) відхилення розміру виготовленої деталі від стандарта стандарта; в) число нестандартних виробів у партії із 100 виробів; г) число очок при одному підкиданні грального кубика.

а) а,б,в; б) в,г; в) а,в,г; г) б,в,г.

2.Чому дорівнює D(CX), де С – стала величина?

а) 1; б) 0; в) С; г) С2.

3.Монету підкидають двічі. Знайти математичне сподівання числа появ герба.

а) 1; б) 1,25; в) 2; г) 0,7.

4.Задана інтегральна функція

0 при x ≤ 0

F(x)= 1 x 3 при 0 < x ≤ 2 ;

8

>1 при x 2

M(X) дорівнює: а) 1/2; б) 7/8; в) 7/8; г) 3/2.

5. Симетричний гральний кубик підкидають 1 раз. Нехай Х – кількість шісток, які при цьому з’являться. Записати функцію розподілу випадкової величини Х.

Тема 5. Закони розподілу та числові характеристики випадкових величин

1. За яким законом розподілена випадкова величина Х, якщо щільність ймовірностей цієї величини має вигляд:

f (x) = 2e−2x , x ≥ 0;

0, x < 0.

136

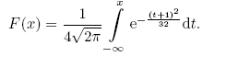
а) рівномірним; б) показниковим; в) нормальним; г) біноміальним.

2. Нормальний закон розподілу випадкової величини Х задано функцією розподілу

Обчислити Р(-5<Х<3).

а) 0,6318; б) 0,9211; в) 0,3124 г) 0,1307.

3. Знайти математичне сподівання та дисперсію випадкової величини, розподіленої за біноміальним законом, якщо n=10, р=0,4.

а) М( Х )=0,1 D( Х )=2,5; б) М( Х )=4 D( Х )=2,4;

в) М( Х )=4 D( Х )=0,04; г) М( Х )=1,5 D( Х )=2,4.

4. Випадкова величина Х розподілена рівномірно в [1; 5]. Знайти її функції щільності та розподілу імовірності.

5.Магазин отримав 10000 пляшок мінеральної води. Імовірність , того, що під час перевезення пляшка виявиться розбитою, дорівнює 0,0004. Знайти ймовірність того, що при перевезенні буде розбито 2 пляшки.

а) 0,0325; б) 1; в) 0,24 г) 0,147.

Тема 6. Багатовимірні випадкові величини

1. Яке з наведених тверджень невірне?

а) 0≤F(x)≤1; б) якщо rxy=0, то Х і Y незалежні; в) rxy ≤1; г) всі вірні.

2.Якщо Кxy=0, то чому дорівнює rxy?

а) -2; б) ∞; в) 1; г) 0.

3.Закон розподілу системи двох випадкових величин Х і Y має вигляд:

137

Знайти М( Х ) і М(Y).

а) М( Х )=1,2 М(Y)=4,3; б) М( Х )=2,6 М(Y)=0,4; в) М( Х )=0,55 М(Y)=1; г) М( Х )=1 М(Y)=1.

4. Задано двовимірний закон розподілу:

5. Ймовірність того, що при перевірці деталь виявиться стандартною, дорівнює 0,7. Перевірці підлягають 2 деталі. Побудувати закон розподілу системи двох дискретних випадкових величин Х – появи числа бракованих деталей і Y – появи числа стандартних деталей.

Тема 7. Функції випадкового аргументу

Неперервна випадкова величина Х задана диференціальною функцією розподілу

Для функції Y = Х2+1 знайти:

1.М(Х). а) 2,11; б) 1; в) 4,5; г) 0.

2.М(Y). а) 61/12; б) –1/12; в) 1,35; г) 14/12 .

3.М(Y2). а) 45,2; б) 87,15; в) 97,87; г) 90.

138

4.D(Y). а) 3,05; б) 72,03; в) 1,71 г) 9,2.

5.σ (Y). а) 0,42; б) 3,03; в) 8,48 г) 1,35.

Тема 8, 9. Граничні теореми теорії ймовірностей

1. Які умови мають виконуватись для нерівності Чебишова?

а) випадкова величина Х має обмежене математичне сподівання; б) випадкова величина Х має обмежену дисперсію;

в) випадкова величина Х має обмежені математичне сподівання і дисперсію; г) випадкова величина Х має обмежені дисперсію і середнє квадратичне.

2. Яке повинна мати значення величина ε у нерівності Чебишова, щобP( X − a < ε) ≈ 0,895 , коли відомо, що D( Х )=3.

а) 0,98; б) 5,35; в) 2,9 г) 4.

3. Випадкова величина Х має закон розподілу N(-2;3). Скориставшись нерівністю Чебишова, оцінити ймовірність |x-a|< ε, якщо ε=5σ.

а) 0,65; б) 0,96; в) 0,895 г) 0,994.

Тема 10, 11. Первинне опрацювання статистичних даних. Статистичне та інтервальне оцінювання параметрів розподілу

1.Якщо додати до всіх варіант вибірки однакове число, то вибіркова середня:

а) помножиться на це число; б) зросте на це число; в) зменшиться на це число; г) не зміниться.

2.Вибіркова сукупність задана таблицею:

139