78

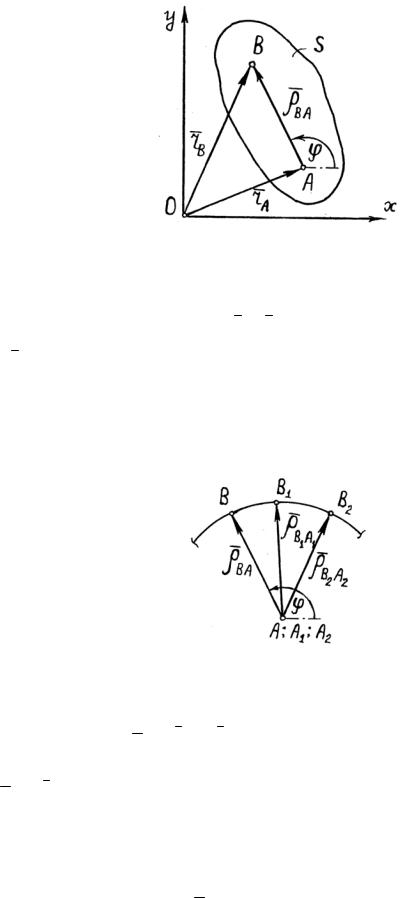
Рис. 2.16

Для произвольной точки В тела имеем

rB rA BA ,

где rA – радиус-вектор полюса А; BA – радиус-вектор точки В, определяющий ее положение относительно полюса А.

Заметим, что движение фигуры S по отношению к системе координат Ах1у1 представляет собой вращение вокруг полюса А (рис. 2.17).

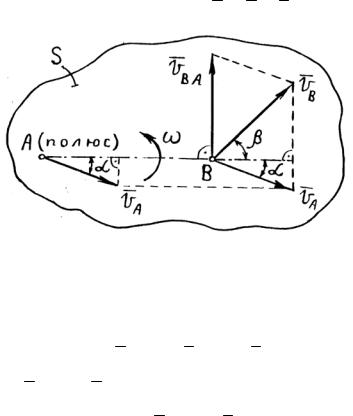
движении вместе с телом вокруг полюса А. Очевидно, что VВА = ωВА и VBA ВА , Где ω – угловая скорость тела.

79

Мы доказали теорему:

Скорость точки тела при плоско – параллельном движении геометрически складывается из скорости какой-нибудь точки, принятой за полюс, и скорости данной точки во вращательном движении вместе с телом вокруг полюса

2.3.5.Теорема о проекциях скоростей двух точек твердого тела на соединяющую их прямую

Теорема. Проекции скоростей двух точек тела на соединяющую их прямую равны между собой.

Доказательство. Известно, что VB VA VBA (рис. 2.18).

Рис. 2.18

Проектируя обе части этого векторного равенства на направление отрезка АВ, получим

ПрАВVB ПрАВVA ПрАВVBA .

Учитывая, что ПрАВVBA 0 (VBA BA ), окончательно получим

ПрАВVB ПрАВVA

или VB cos VA cos .

80

2.3.6.Мгновенный центр скоростей и общий случай определения его положения. Определение скоростей точек тела с помощью мгновенного центра

скоростей

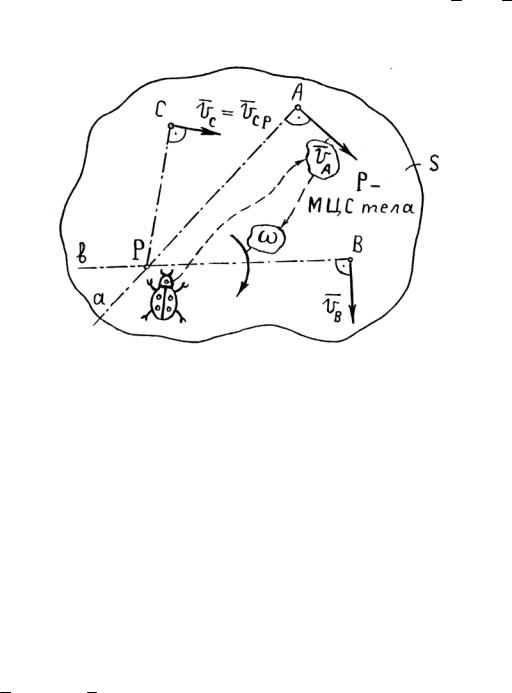
Мгновенным центром скоростей (МЦС) называется точка тела, скорость которой в данный момент времени равна нулю.

Пусть в некоторый момент времени точки А и В тела имеют VA и VB , не параллельные друг другу (рис. 2.19).

Рис. 2.19

Вектор скорости точки А известен по величине и по направлению; вектор скорости точки В известен только по направлению.

Докажем, что точка Р, лежащая на пересечении перпендикуляров Аа и Вв

Случай VР АР и VР ВР исключается.