Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российская открытая академия транспорта МИИТ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции по Теоретической механике.pdf

Скачиваний:

381

Добавлен:

03.03.2016

Размер:

3.26 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1313

Ч а с т ь 3 Д И Н А М И К А

Глава 3.1 Динамика материальной точки

Введение в динамику

Динамикой называется раздел теоретической механики, в котором изучается движение материальных тел под действием приложенных сил.

Закономерности механического движения материальных тел изучаются при помощи формирования физических и общих понятий и при помощи построения физических и математических моделей.

Простейшей физической моделью материального тела является материальная точка, в которой из всех свойств тела учитывается только ее масса. Более сложные материальные объекты считают состоящими из материальных точек.

Самая фундаментальная проблема, остававшаяся в течение тысячи лет неразрешимой из-за ее сложности – это проблема движения. Впервые ответы на главные вопросы этой проблемы были даны Исааком Ньютоном (1642 – 1727 гг.) в его классическом произведении «Математические начала натуральной философии» (1687 г.).

«Начала» являются одним из крупнейших достижений в области естествознания за всю историю их развития. Они содержат дедуктивную систему механики, построенную на основе аксиоматического метода. Классическая механика покоится на аксиомах, которые называют законами Ньютона, а также на открытом им законе всемирного тяготения.

Ньютон в «Началах» показал, что очень просто сформулированные законы после применения к ним соответствующих математических преобразований могут количественно описывать сложные явления природы. Впервые было ярко показано могущество математического естествознания.

Сохранилось большое число черновых набросков законов Ньютона, свидетельствующих о том, насколько тщательно он обдумывал каждую словесную формулировку. Большая заслуга Ньютона в том, что он

формулировал аксиомы динамики ясно и кратко, а ясность и краткость существенно помогают правильному мышлению.

Возникновение динамики в ее современном виде явилось результатом одновременного качественного скачка сразу в двух отношениях. Во-первых, характеристики движения тел были сформулированы как математические понятия. И, во-вторых, было создано дифференциальное и интегральное исчисление, с помощью которого стало возможным выразить законы движения и равновесия твердых, жидких и газообразных тел, составляющих основы механики (акад. Ишлинский А.Ю.).

Нам хочется думать, и мы надеемся, что настоящее учебное пособие окажется полезным для студентов, изучающих теоретическую механику.

Рисунки к учебному пособию выполнены автором профессором Капрановым И.В.

3.1.1.Аксиомы (законы) динамики

В основу динамики как науки положены аксиомы, которые получены в результате обобщения опыта и наблюдений над движущимися телами. Аксиомы были впервые систематически изложены Ньютоном в его труде «Математические начала натуральной философии» (1687г.).

Аксиома первая (закон инерции)

Изолированная материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения (рис. 3. 1)

Рис. 3.1

100

Закон инерции был впервые установлен Галилеем (1654 – 1642 гг.). До него господствовало мнение, что движение может быть вызвано только непрерывным воздействием силы, то есть движение без силы невозможно. Предшественники Галилея связывали силу со скоростью движущегося тела. Галилей первый поставил понятие силы в связь с изменением скорости, то есть с ускорением.

Хотя Галилей и пришел к этому закону раньше Ньютона (1638 г.), но сформулировал его как следствие из проведенных им опытов по падению тел по наклонной плоскости. Ньютон поставил закон инерции во главу угла системы аксиом (законов) динамики.

Изолированная материальная точка («одинокая во всей Вселенной») – это абстрактное понятие. Прямолинейное и равномерное движение свободной материальной точки (тела) в природе не наблюдается – это еще одно абстрактное понятие.

Парадоксальность неограниченно сохраняющегося прямолинейного движения тела с постоянной скоростью очень долго мешала открытию закона инерции.

Отклонение точки от «идеальной» прямолинейной траектории и «идеального» равномерного движения будут происходить под действием приложенной к ней силы.

Сила для точки является внешней причиной изменения скорости, так как точка самостоятельно не может ее изменить. Ускорение точки является мерой отклонения от равномерного и прямолинейного движения, то есть отклонения точки от движения по инерции.

Закон инерции означал, что причинный закон движения должен быть установлен с помощью ускорения, то есть изменения скорости по величине, направлению или в обоих отношениях. Основополагающее значение ускорения является самым незыблемым и самым блистательным из всех открытий Галилея (Джон Берналл).

Вторая аксиома (основной закон динамики материальной точки)

101

Имеет место векторное равенство (рис. 3. 2)

Рис. 3.2

ma		,	(3.1)
	F
где m – масса точки; a – ее ускорение;					– сила, приложенная к точке.
				F

Произведение массы точки на ускорение, которое точка приобретает под действием приложенной к ней силы, равно по величине этой силе, а направление ускорения совпадает с направлением силы (рис. 3.2).

Равенство (3.1) называется основным законом динамики точки. Третья аксиома (закон равенства действия и противодействия)

Силы взаимодействия двух материальных точек равны по величине и противоположны по направлению (рис. 3.3).

Рис. 3.3

F2 F1 ,

102

где F1 - сила, с которой точка В2 действует на точку В1;

F2 - сила, с которой точка В1 действует на точку В2.

В природе силы встречаются всегда попарно. Падающий камень притягивает Землю с такой же силой, как и Земля притягивает камень.

Ньютон иллюстрирует третью аксиому несколькими примерами. Приведем один из них. «Если кто нажимает пальцем на камень, то и палец его нажимается камнем…».

Эта аксиома делает возможным переход от отдельной материальной точки к механике сложных материальных систем; в частности, эта аксиома лежит в основе статики строительных конструкций.

Четвертая аксиома (закон суперпозиции или закон независимости действия сил)

Ускорение, приобретаемое материальной точкой от действия нескольких сил, равно геометрической сумме тех ускорений, которые она приобретала бы от каждой силы, действующей отдельно и независимо от других.

Эта аксиома не является независимой, а вытекает из аксиомы сложения двух

сил по правилу параллелограмма.

Пусть к материальной точке приложена

система сил

F1 , F2 ,..., Fn . На

основании второй и затем четвертой аксиомы соответственно имеем

F1 ma1 ;

F2 ma2 ; …,

Fn man ;

a a1 a2 ... an .

Далее получаем

ma ma1 ma2 ... man F1 F2 ... Fn

или
ma FK .	(3.2)

Уравнение (3.2) называют основным законом динамики в случае действия на точку нескольких сил.

103

3.1.2.Инерциальная система отсчета Говоря о движении, необходимо иметь в виду определенную систему

отсчета, то есть систему координат, скрепленную с телом.

Сила, как мера механического воздействия материальных тел, не зависит от выбора системы отсчета. Ускорение зависит от выбора системы отсчета (см. теорему Кориолиса о сложении ускорения точки в сложном движении). Отсюда следует, что аксиомы динамики не могут быть справедливыми в любой системе отсчета.

Введем следующее определение.

Система отсчета называется инерциальной, если в ней справедливы аксиомы Ньютона.

На практике с достаточной степенью точности считается инерциальной система отсчета, связанная с Землей.

3.1.3.Дифференциальные уравнения движения материальной точки в проекциях на оси прямоугольной декартовой системы координат

Не будем делать различия между свободной и несвободной материальной точками. Пусть F – равнодействующая активных сил и реакций связей.

В статике все силы считают постоянными. В динамике почти все силы являются переменными. В общем случае приложенная к точке сила может зависеть от времени, положения точки и ее скорости, то есть

F F (t, r , v) ,

где t – время;	r	- радиус-вектор точки;				v - ее скорость.
Дифференциальное уравнение движения точки в векторной форме имеет вид
(рис. 3.2)
		m d 2	r		,	(3.3)
				F
		dt 2

104

где ddt22r a – ускорение точки.

Воспользуемся кинематическими зависимостями

a	X	dvX	d 2 x	и т.д.
		dt	dt2

a(aX , aY , aZ ) ;			v(vX , vY , vZ ) .

Проектируя обе части равенства (3.3) на оси координат Охуz, получим искомые дифференциальные уравнения движения точки

md 22x FX ; dt

m d 2 2y FY ; dt

m	d 2 z	FZ .	(3.4)
	dt 2

3.1.4.Дифференциальные уравнения движения материальной точки в проекциях на оси подвижной естественной системы координат

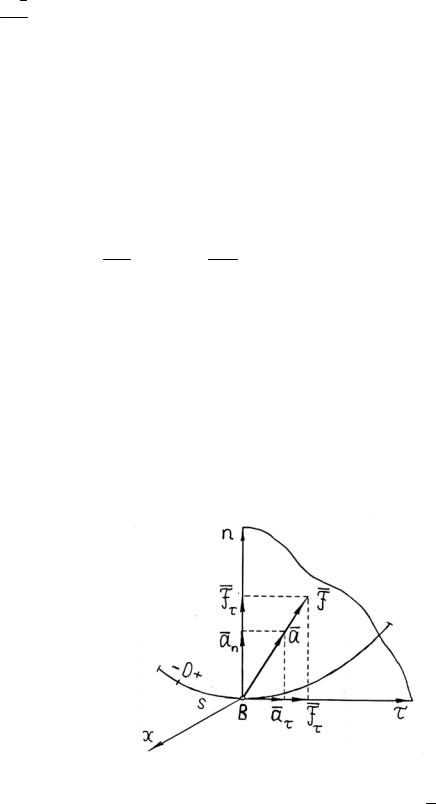
Для получения искомых уравнений спроектируем обе части равенства (3.1) на оси подвижной естественной системы координат Вτnb (Вτ – касательная к траектории точки; Вn – главная нормаль; Вb – бинормаль) (рис. 3.4).

Рис. 3.4

ma F ; man Fn ; mab Fb ; a a , an , ab ; F F , Fn , Fb .

Учитывая кинематические зависимости

a	dv ;	an	v2	; аb = 0,

	dt

получим

105

m dv	F ,	m v2	Fn ; 0 = Fb ,	(3.5)
dt

где ρ – радиус кривизны траектории точки.

Уравнения (3.5) представляют собой дифференциальные уравнения движения точки в проекциях на оси подвижной естественной системы координат.

3.1.5.Первая основная задача динамики материальной точки

Найти силу по заданному движению точки.

Рассмотрим решение этой задачи в прямоугольной декартовой системе координат.

Известны масса точки и закон ее движения вдоль траектории в виде

х = х (t), у = у (t), z = z (t),

где х, у, z – координаты движущейся точки.

Проекции силы на оси координат найдем с помощью дифференциальных уравнений движения точки

	;		;		,
Fx m x		Fy m y		Fz m z

где x ddt22x и т.д.

Зная проекции силы на ось координат, находим величину силы и косинусы углов силы с осями координат

F	Fx2 Fy2 Fz2 ;	cos		,^ x	Fx	и т.д.
			F
					F

3.1.6.Вторая основная задача динамики материальной точки

Найти движение точки по заданной силе.

Известны масса точки и закон изменения приложенной к точке силы

F F (t, r,v) .

106

Решение второй или обратной задачи динамики точки приводит к математической задаче: проинтегрировать систему трех дифференциальных уравнений второго порядка (3.4), разрешенных относительно вторых производных; аргументом является время t, а неизвестные функции – это координаты х, у, z движущейся точки, которые надо найти в функции времени.

Рассмотрим решение поставленной задачи в случае прямолинейного движения точки вдоль оси Ох.

Дифференциальное уравнение движения точки и его общее решение имеют

вид

			(3.6)		,C2 ) ,	(3.7)
m x	Fx (t, x, x)		(3.6)	x f (t,C1	,C2 ) ,	(3.7)
где С1 и С2 – постоянные интегрирования.
Проекция вектора скорости точки на ось Ох
				,C2 )	(3.8)
		Vx x f (0,C1		,C2 )	(3.8)

Задание силы не определяет конкретного вида движения точки, а выделяет целый класс движений, характеризующийся двумя произвольными постоянными.

Задание силы определяет только ускорение движущейся точки, а положение точки на траектории и ее скорость зависят от начального положения точки и от начальной скорости точки.

Для определения конкретного вида движения точки необходимо задать так

называемые начальные условия движения точки:

при

t = 0

r0 и

(3.9)

или при

t = 0

х = х0

(3.9')

Vx0

Подставив начальные условия (3.9') в уравнения (3.7) и (3.8), получим два

алгебраических уравнения с двумя неизвестными С1 и С2.

f (0,C1 ,C2 ) ;

(3.10)

Vx0

f (0,C1 ,C2 )

(3.11)

107

Если система уравнений (3.10) и (3.11) разрешима, то из нее можно найти указанные произвольные постоянные; подставив найденные значения С1 и С2 в общее решение (3.7), мы получим частное решение

x f (t,t0 , x0 , x0 ) .

Решение второй задачи динамики точки вызывает значительные трудности. Для некоторых случаев задания силы мы не можем построить общее решение

системы дифференциальных уравнений движения точки.

Если мы не можем этого сделать, следует решать задачу приближенными методами – либо методами численного интегрирования, либо при помощи вычислений на электронных счетных машинах (сразу ищем частное решение при заданных начальных условиях). Серьезным недостатком численных методов является то, что для других начальных условий надо вновь искать частное решение; общее же решение содержит в себе все частные решения при любых начальных условиях.

3.1.7.Дифференциальное уравнение относительного движения материальной точки

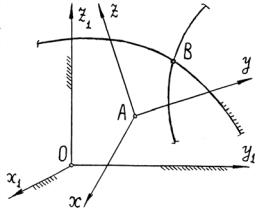
Имеем инерциальную систему отсчета Ох1у1z1 и материальную точку В массой m, к которой приложена сила F – равнодействующая активных сил и реакций связей.

Рассмотрим движение точки В относительно подвижной системы отсчета Охуz, движущейся произвольным образом по отношению к инерциальной системе отсчета Ах1у1z1 (рис. 3.5).

108

Рис. 3.5

В инерциальной системе отсчета справедлив основной закон динамики точки (уравнение движения точки в векторной форме)

ma		(3.1)
	F

По теореме о сложении ускорений точки в сложном движении имеем

a aOTH aПЕР аКОР ,

где a, aOTH , aПЕР , аКОР – соответственно абсолютное, относительное, переносное ускорение точки и ускорение Кориолиса.

После подстановки значения абсолютного ускорения в уравнение (3.1) получим

maOTH

( maПЕР ) ( maKOP )

или maOTH

ПЕР

KOP ,

(3.12)

где

ПЕР maПЕР

KOP maKOP .

Векторы

ПЕР и

KOP называются соответственно переносной силой инерции

и силой инерции Кориолиса.

Уравнение (3.12) представляет собой дифференциальное уравнение относительного движения точки в векторной форме.

Материальная точка движется относительно неинерциальной системы отсчета так же, как и относительно инерциальной, если к приложенным активным силам и реакциям связей добавить переносную и кориолисову силы инерции.

109

Итак, действующая на точку сила и создающая ее относительное ускорение, состоит из трех сил: непосредственно приложенной к точке силы ( F ) и двух дополнительных сил, наблюдаемых только в подвижной системе отсчета.

В неинерциальной системе отсчета Охуz основной закон динамики точки в простейшей форме (3.1) не выполняется.

Переносная и кориолисова силы инерции относятся к особой категории сил. Для этих сил мы не можем указать источник их возникновения в виде другого тела или точки. По этой причине указанные силы инерции не подчиняются третьей аксиоме Ньютона – закону равенства действия и противодействия. Их возникновение обусловлено движением точки вместе с подвижной системой отсчета Охуz по отношению к инерциальной системе отсчета Ах1у1z1.

3.1.8.Частные случаи

Относительное движение по инерции Движение материальной точки прямолинейно и равномерно относительно

подвижной системы отсчета называется относительным движением по инерции.

_______
В этом случае VOTH const и aOTH 0 .
Из (3.12) получаем условие для сил при относительном движении точки по
инерции
F ФПЕР ФКОР 0 .	(3.13)

Относительное равновесие При равновесии (покое) материальной точки относительно подвижной

OTH 0 , aOTH

0 и

0 .

системы отсчета имеем V

aKOP 2

VOTH

Из (3.12) вытекает условие относительного равновесия для сил

ПЕР

0 .

(3.14)

Условие относительного равновесия для сил отличается от условия относительного движения по инерции.

110

3.1.9.Принцип относительности Галилея – Ньютона

Пусть подвижная система отсчета Охуz движется по отношению к инерциальной системе отсчета Ах1у1z1 поступательно, равномерно и прямолинейно. В этом случае переносная и кориолисова силы инерции равны нулю, то есть

ФПЕР maПЕР 0 , ФКОР maКОР 0 .

Уравнение относительного движения точки

maOTH F

совпадает с уравнением ее движения относительно инерциальной («привилегированной») системы отсчета.

Все подвижные системы отсчета, которые движутся поступательно, равномерно и прямолинейно относительно основной инерциальной системы отсчета, также являются инерциальными.

В основе принципа Галилея – Ньютона лежит отсутствие принципиальной возможности каким-либо механическим опытом, основанном на наблюдении за движением материальных тел, отличить одну инерциальную систему отсчета от другой.

Этот принцип утверждает:

Никаким механическим опытом наблюдателю невозможно установить факт инерциального движения системы отсчета, в которой наблюдатель находится; все механические явления в различных инерциальных системах отсчета протекают одинаково.

Наблюдатель в корабле, движущемся поступательно, равномерно и прямолинейно, не может установить «движется корабль или стоит неподвижно» (Галилей).

111

Глава 3.2. Материальная система – силы и центр масс.

Моменты инерции твердого тела

3.2.1.Материальная система. Принцип освобождаемости от связей. Внешние

ивнутренние силы

Встатике и кинематике мы рассматривали точки и абсолютно твердые тела;

вдинамике мы рассмотрим гораздо более общий объект – так называемую материальную систему.

Материальной системой или системой материальных точек называется такая их совокупность, в которой движение каждой точки зависит от положения и движения всех остальных точек.

Точки материальной системы взаимодействуют друг с другом и поэтому их движения взаимно связаны.

Примеры материальных систем: абсолютно твердое тело, упругое тело, машинный агрегат, живое существо, Солнечная система и т.д.

Вобщем случае материальной системы силу следует считать не скользящим, а связанным вектором – она приложена к данной точке системы и ее никуда нельзя переносить.

Всякую несвободную материальную систему мы можем рассматривать как свободную, если все ее точки освободить от связей и приложить к ним реакции связей ( принцип освобождаемости от связей).

Внешними называются силы взаимодействия точек данной системы с точками других систем.

Внутренними называются силы взаимодействия между точками данной системы.

Обозначение внешней силы – F e , внутренней силы – F i . Отметим следующие свойства внутренних сил.

Первое свойство. Главный вектор внутренних сил системы равен нулю.

112

Второе свойство.

Главный момент внутренних сил системы относительно любой точки (или оси) равен нулю.

Силы взаимодействия двух точек системы равнопротивоположны и лежат на одной прямой (по закону равенства действия и противодействия), поэтому

R i FKi 0 и M 0i m0 (FKi ) 0 .

3.2.2.Масса материальной системы и ее центр масс

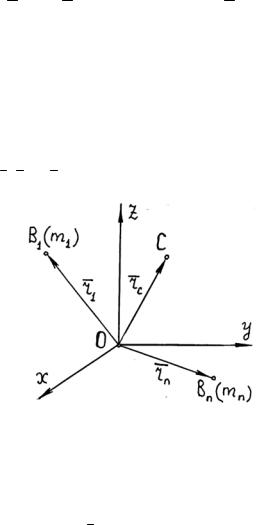
Пусть мы имеем систему, состоящую из n точек В1 (m1), В2 (m2), …, Вn (mn), радиус-векторы которых r1 , r2 ,..., rn (рис. 3.6).

Рис. 3.6

Массой системы называется сумма масс всех ее точек M mK .

Центром масс системы называется точка, радиус-вектор которой

	mK	rK	.	(3.15)
rC
	M

Координаты центра масс системы (точки С)

xC	mK xK	, yC	mK yK	, zC	mK zK	.	(3.16)
	M		M		M

Пусть система находится вблизи поверхности Земли. Умножим числитель и знаменатель каждой из дробей на ускорение свободного падения g. Формулы (3.16) приобретают вид

xC	рK xK	, уC	рK уK	, zC	pK zK	,	(3.17)
	Р		Р		P

113

где рК = mК g – сила тяжести к-ой точки системы; Р= Мg – сила тяжести системы.

Итак, если система находится вблизи поверхности Земли, то ее центр масс совпадает с центром тяжести (при условии, что система отвердела и стала абсолютно твердым телом).

3.2.3.Дифференциальные уравнения движения материальной системы

Приложим к каждой точке системы равнодействующую внешних сил FКе и равнодействующую внутренних сил FKi . Составим дифференциальное уравнение движения к-ой точки системы в векторной форме

	d 2	r
mK	d 2	r	FKe FKi ; к = 1, 2, …, n.
mK		K	FKe FKi ; к = 1, 2, …, n.
	dt

Мы получили дифференциальные уравнения движения системы в векторной форме. Если спроектировать эти уравнения на оси прямоугольной декартовой системы координат, то получим систему 3n дифференциальных уравнений, описывающих движение всех точек материальной системы.

3.2.4.Моменты инерции тел вращения

Моментом инерции тела относительно центра называется сумма произведений масс всех точек тела на квадраты их расстояний до данного центра

I0 mK rK2 mK (xK2 yK2 zK2 ) ,

где (хК, уК, zК) – координаты к-ой точки тела.

Моментом инерции тела относительно оси называется сумма произведений масс всех точек тела на квадраты их расстояний до данной оси

I Z mK KZ2 mK (xK2 yK2 ) и т.д.

Имеет место зависимость

2I0 I x I y I z .

> I zC .

114

Радиусом инерции тела относительно оси называется расстояние от оси такой воображаемой материальной точки, масса которой равна массе тела, а момент инерции относительно оси равен моменту инерции тела относительно той же оси

I z miz2 ,

где iz – радиус инерции тела относительно оси Оz.

3.2.5 Теорема Гюйгенса – Штейнера (о зависимости между моментами инерции твердого тела относительно параллельных осей).

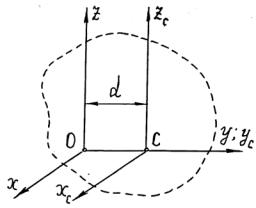
Момент инерции тела относительно некоторой оси равен сумме момента инерции тела относительно параллельной оси, проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями (рис. 3.7).

Рис. 3.7

I x I xC Md 2 ; I z I zC Md 2 .

Очевидно, что I x > I xC и I z

Моменты инерции простейших однородных тел приведены в таблице 3.1.

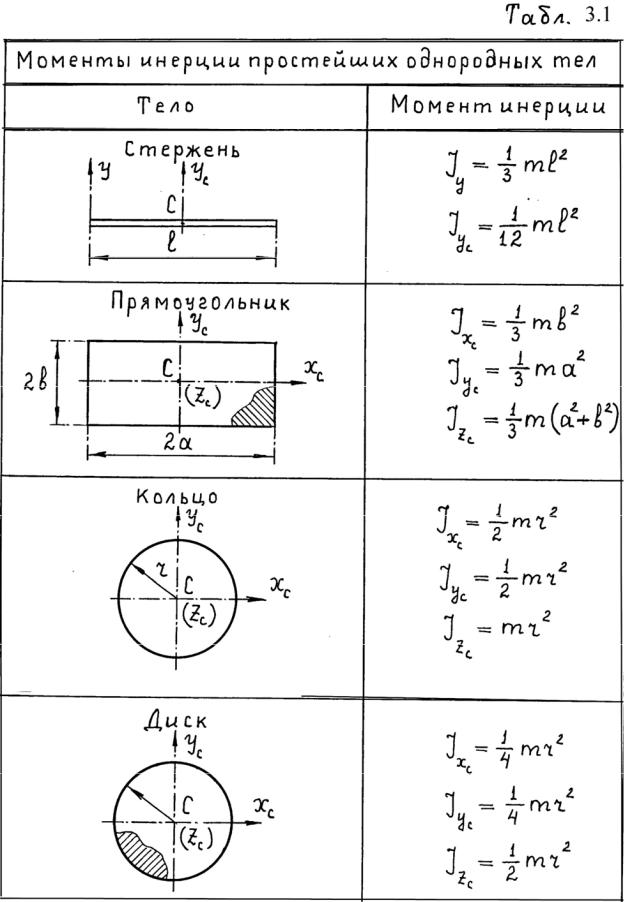
115

116

Глава 3.3. Теорема об изменении кинетической энергии

3.3.1.Кинетическая энергия материальной точки и материальной системы

Кинетической энергией точки называют половину произведения массы точки на квадрат ее скорости

mV2 2 mV2 2 ,

так как V 2 V V V V cos V ,^ V V 2 .

Кинетической энергией системы называют сумму кинетических энергий всех ее точек

Т mK2VK2 .

Кинетическая энергия как точки, так и системы не зависит от направления скоростей точек.

3.3.2.Кинетическая энергия твердого тела при поступательном, вращательном и плоскопараллельном движении

а)Поступательное движение тела Кинетическая энергия тела при поступательном движении

mKVK2

mKVC2

VC2

1 MV 2

где V1 = V2 = … = Vn = Vс = V – скорость центра масс тела или скорость его

поступательного движения.

Итак, Т

1 MVC2 ,

(3.18)

где М= mK – масса тела.

б)Вращательное движение тела Кинетическая энергия тела при вращательном движении (рис.3 8)

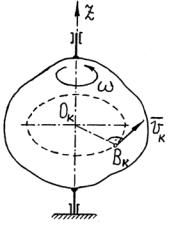
117

Рис.3.8

mKVK2

mK ( KZ )2

1 I

где

I Z mK KZ2

– момент инерции тела относительно оси вращения Оz;

VK KZ

– скорость

к-ой точки тела; ρКZ

–

расстояние

этой

точки до оси

вращения; ω – угловая скорость тела.

Итак, Т 1

I Z 2 .

(3.19)

Из сравнения формул (3.18) и (3.19) следует, что эти формулы подобны. При вращательном движении тела аналогом массы является момент инерции тела относительно оси вращения.

в)Плоско – параллельное движение тела Плоско – параллельное движение тела состоит из поступательного движения

вместе с полюсом и вращательного движения вокруг оси, проходящей через полюс перпендикулярно плоскости движения тела.

Примем за полюс центр масс тела (точку С). Кинетическая энергия тела при плоско – параллельном движении (рис.3.9)

118

			Рис.3.9
Т	1 MVC2	I ZC 2 ,	(3.20)
	2

где I ZC – момент инерции тела относительно оси ZС, проходящей через центр масс тела перпендикулярно плоскости движения; ω – угловая скорость тела.

3.3.Элементарная и полная работа силы

Работа – физическая величина, являющаяся мерой превращения кинетической энергии. Работа измеряет либо кинетическую энергию, возникшую из других форм энергии, либо кинетическую энергию, превратившуюся в другие формы энергии.

Работа силы на каком-либо перемещении является характеристикой действия силы на этом перемещении.

Элементарной работой силы называется работа, выполняемая силой на элементарном перемещении точки ее приложения (рис.3.10)

dA(		)			(3.21)
	F		F	dr

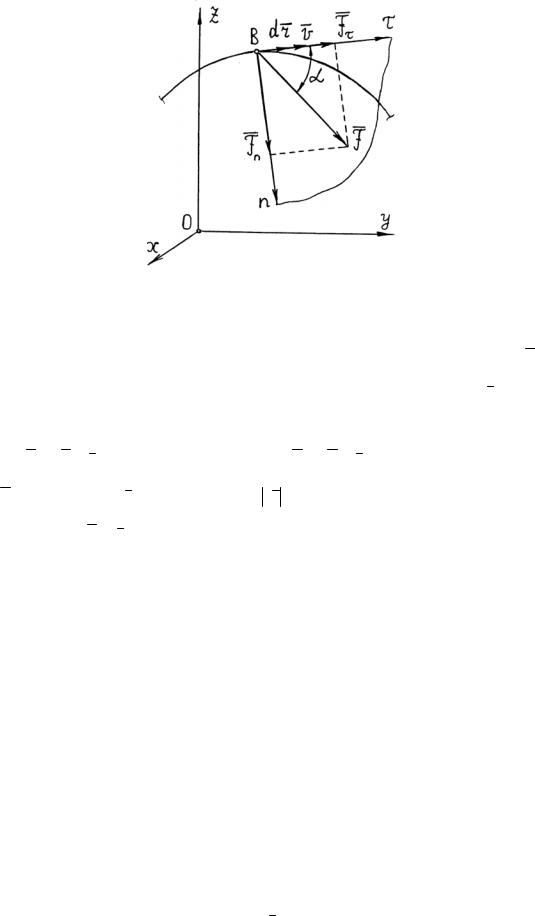
119

Рис. 3.10

Элементарная работа силы равна скалярному произведению силы (F ) на вектор элементарного перемещения точки ее приложения (dr ) .

На основании (3.21) получаем (рис. 3.10)

dA(F ) F dr Fx dx Fy dy Fz dz ; dA(F ) F dr Fds cos F ds , (3.22)

где F (Fx , Fy , Fz ) и dr (dx, dy, dz) ; ds dr ; s OB (криволинейная координата точки В); F F cos F ,^ dr F cos .

Пусть точка приложения силы перемещается вдоль некоторой траектории от начальной точки В0 до конечной точки В1.

Работой силы на конечном перемещении точки ее приложения называется сумма соответствующих элементарных работ.

Полная работа силы равна криволинейному интегралу, вычисленному вдоль дуги траектории точки приложения силы (от точки М0 до точки М1).

В1

А dA .

В0

Мощностью силы называется скорость изменения элементарной работы в данный момент времени

	dA
N		F	dr			F V .
		F	dr	F	V
	dt		dt	F	V
	dt		dt

120

Мощность равна произведению касательной составляющей силы на скорость точки ее приложения.

3.4.Формулы для вычисления работы некоторых сил

а)Работа, выполняемая силой тяжести

Силу тяжести материальной точки массой m вблизи поверхности Земли можно считать постоянной и направленной по вертикали вниз.

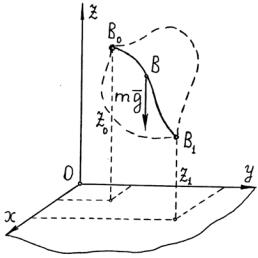
Работа силы тяжести (рис. 3.11)

A(mg) mgdz mg(z1 z0 ) mgh ,

где z1 z0 h – высота опускания (подъема) точки по вертикали.

Рис.3.11

Очевидно, что работа силы тяжести не зависит от формы траектории точки приложения данной силы.

Силы, обладающие указанным выше свойством, называются потенциальными.

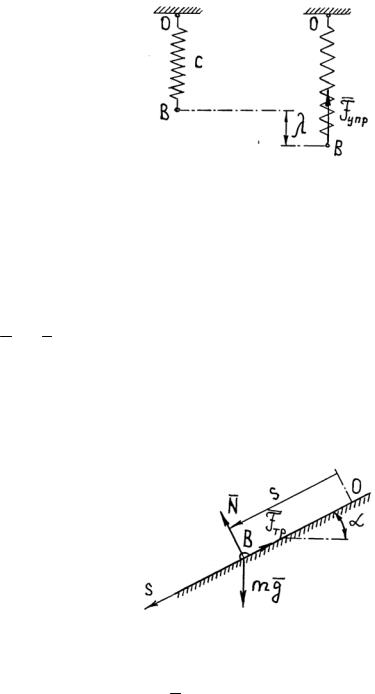
б)Работа линейной силы упругости Рассмотрим пружину, показанную на рис. 3.12. При растяжении или сжатии

пружины возникает сила упругости (восстанавливающая сила), стремящаяся вернуть пружину в положение равновесия, когда ее деформация равна нулю. Эта сила определяется по формуле (рис. 3.12)

121

FУПР с ,

где с – жесткость пружины; λ – ее деформация. Работа силы упругости

				1 c 2 .
A(		УПР ) FУПРd c d
	F
0			0	2

Заметим, что А (FУПР) > 0 или А (FУПР) < 0.

Рис.3.12

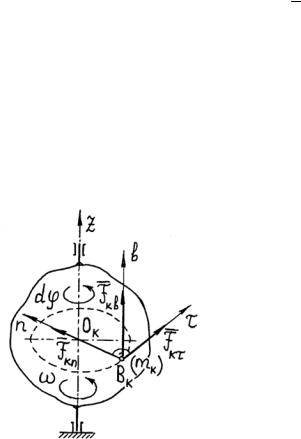
в)Работа, выполняемая силой сухого трения

Пусть материальная точка (тело) массой m перемещается по наклонной шероховатой плоскости с углом α на расстояние s (рис. 3.13). На точку действуют силы mg , N и FTP (сила тяжести, нормальная реакция плоскости и сила трения, направленная противоположно перемещению точки), причем

N = mg соs α; FТР = fN = f mg соs α,

где f – коэффициент трения между точкой и плоскостью.

Рис.3.13

Работа силы трения

А(FTP ) FTP s ( fmg cos )s .

Работа силы трения всегда отрицательна.

122

3.5.Работа сил, приложенных к вращающемуся твердому телу

Пусть к вращающемуся телу в точке ВК приложена сила FK ; расстояние

ОКВК = ρkz (рис. 3.14). Разложим силу

Kn и

по осям

FK на составляющие Fk ,

ВКτК , ВКnК и ВКbК . Элементарная работа указанной силы

dA(

FK ) FK dsK FK KZ d mZ (FK )d ,

где

dsK KZ d ; d – элементарный угол поворота тела;

mZ (

момент

FK ) –

силы

относительно оси вращения Оz.

				Рис. 3.14
Работа приложенных к телу сил (
				F1 , F2 ,..., Fn )

A 1	mZ (		1
		FK )d M Z d M Z ( 1 0 ) M Z ,
0	0

где (φ1 – φ0) = φ – угол поворота тела.

Работа сил, приложенных к вращающемуся твердому телу, равна произведению главного момента этих сил относительно оси вращения на угол поворота тела.

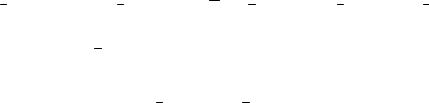
123

3.6.Теорема об изменении кинетической энергии Вычислим дифференциал кинетической энергии

mKVK

drK

mKVK

dT d

2VK dVK

mKVK dVK

dVK

drK mK aK drK

FKi drK

FKe

FKe drK FKi drK ,

где

dVK

aK ; mK aK

VK ;

FKe FKi .

Итак, dT

(3.23)

FKe drK FKi drK .

Формула (3.23) выражает теорему об изменении кинетической энергии системы в дифференциальной форме.

Дифференциал от кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.

Из формулы (3.23) путем интегрирования получим

Т Т0 АКе АКi , (3.24)

где Т и Т0 – кинетическая энергия системы в конечном и начальном положении;

АКе и АКi – сумма работ внешних сил и сумма работ внутренних сил при перемещении системы из начального положения в конечное положение.

Формула (3.24) выражает теорему об изменении кинетической энергии системы в конечной или дифференциальной форме.

Изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, вычисленных на соответствующих перемещениях точек их приложения.

Частный случай Для абсолютно твердого тела сумма работ внутренних сил равна нулю

AKi 0 .

Изменение кинетической энергии твердого тела при перемещении из одного положения в другое равно сумме работ внешних сил, вычисленных на соответствующих перемещениях точек их приложения.

124

Т Т0

АКе .

(3.25)

Глава 4. Теорема об изменении количества движения и теорема о движении центра масс

4.1 Количество движения материальной точки и материальной системы

Количеством движения точки называется вектор, равный

произведению массы точки на вектор ее скорости

;

(3.26)

q mV

(Vx ,Vy ,Vz )

qx mVx и т.д.

q(qx ,qy ,qz ); V

(3.27)

Количеством движения системы называется сумма количеств

движения всех точек системы

Qx mVx

(3.28)

(Vx ,Vy ,Vz )

Qx mxVkx

и т.д. (3.29)

(Qx ,Qy ,Qz ); V

Вычислим количество движения системы

mк

( mk

rk )

(Mrc ) M

mxVk

MVc

, (3.30)

где mx

rk Mrc ;

- скорость центра масс С;

rк

- скорость k-ой точки системы.

Итак,

(3.31)

Количество движения системы равно количеству движения центра масс при условии, что в центре масс сосредоточена вся масса системы.

4.2 Теорема об изменении количества движения

Вычислим производную по времени от количества движения системы

125

mк

dVk

( mk ak ) (

( mxVk

)

Fke Fki ) Fke ,

где aк

dVк

- ускорение k-ой точки системы;

mk aк

Fke Fki ;

Fki 0 (по свойству внутренних сил системы).

Окончательно имеем

dQx

Fkxe и т.д. (3.32); (3.33)

Fke

Производная по времени от количества движения системы равна сумме всех внешних сил, приложенных к точкам системы

4.3 3аконы сохранения количества движения системы Возможны два частных случая.

1) Если Fke 0 ,то ddtQ 0 и Q const Q0

(закон сохранения вектора количества движения системы).

2) В случае, когда Fkxe 0 , получаем dQdtx 0 и Qx const Qx0 (закон сохранения вектора количества движения системы).

4.4 Теорема о движении центра масс Следствием теоремы об изменении количества движения системы является теорема о движении центра масс Воспользуемся зависимостями

Qc MVc M d

(3.34) и

.(3.35)

Fke

После подстановки (3.34) в (3.35) получаем

Mac

; Macy Fkye ; Macz

Fkze , (3.36)

Fke ; Macx Fkxe

где aс

dVс

- ускорение центра масс С; aс (acx , acy , acz ).

126

Центр масс системы движется как свободная материальная точка, в которой как бы сосредоточена вся масса системы и к которой как бы приложены все внешние силы, действующие на систему.

4.5 Законы сохранения скорости, положения и координаты центра масс

Рассмотрим частные случаи:

Если

то

Mаc

dVc

Fke 0,

const Vco

(закон сохранения скорости центра масс).

В случае, когда

Fke

Vc Vco 0 получаем

const

(закон сохранения положения центра

масс).

Если

Fkxe

то

Mаcx M

dVcx

и Vcx const Vcx / o

(закон сохранения проекции скорости центра масс).

В случае, когда Fсчe

Vcч Vcх/ o 0 получаем

dхc

const

(закон

сохранения координаты

cх

центра масс).

4.6 Дифференциальные уравнения поступательного движения твердого тела

При поступательном движении тела скорости и ускорения всех его точек соответственно геометрически равны между собой

V1 V2 Vn Vc V ; a1 a2 an ac a,

127

где V и а - скорость и ускорение тела.

Из теоремы о движении центра масс (3.36) получим дифференциальное уравнение поступательного движения тела в векторной форме


	Ma			a(àx ,ay ,az ) (3.37)
	Ma		Fke ;	a(àx ,ay ,az ) (3.37)
В проекциях на оси координат имеем
Mx	Fkxe ;	My		Fkye ;	Mz Fkze ; (3.38)

где x, y, z -координаты произвольной точки тела; x, y, z проекции ускорений этой точки на оси координат( x аx , y ay , z az ).

Дифференциальные уравнения поступательного движения тела аналогичны дифференциальным уравнениям движения одной точки.

Глава 5 Теорема об изменении кинетического момента

5.1 Кинетический момент материальной точки и материальной системы

Кинетическим моментом материальной точки относительно некоторого центра называется векторный момент количества движения точки относительно этого центра (рис. 3.14)



ko mo (mV	)	r	mV ,	(3.39)

где r радиус вектор точки относительно центра О; mV -количество движения точки.

128

Рис.3.14

Кинетический момент материальной системы относительно центра


	K	o mo (mkVk )			rk mkVk .			(3.40)

Кинетическим моментом материальной точки относительно некоторой оси называется момент количества движения точки относительно этой оси

		) и т.д.	(3.41)
kz mz (mV

Кинетический момент материальной системы относительно оси

Kz mz (mkVk ) и т.д. (3.42)

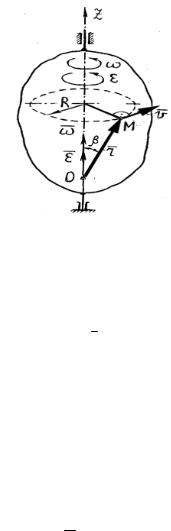
5.2 Кинетический момент относительно оси вращения при вращательном движении твердого тела

Вычислим кинетический момент тела относительно оси вращения Oz, когда тело вращается с угловой скоростью (рис.3.15 )

129

Рис.3.15

Kz mz (mkVk ) (mkVk ) kz (mk kz ) kz mk kz 2 I z ,

где Vk kz	-скорость k -ой точки тела;
kz - расстояние этой точки до оси Оz;
I z mk kz	2 - момент инерции тела относительно оси Oz.
Итак Kz Iz .		(3.43)

Кинетический момент тела относительно оси равен произведению угловой скорости тела на момент его инерции относительно оси вращения. Знак кинетического момента относительно оси вращения совпадает со знаком угловой скорости тела вокруг этой оси.

5.3Теорема об изменении кинетического момента

Вычислим производную по времени от кинетического момента материальной системы относительно центра

] [

[

mkVk

(mkVk

)]

(

rk mk

) (

rk mk ak )

[rk (Fke Fki )] (rk Fke ) mo (Fke ),

130

где

dVk

i ;

m V

dt k

k k

rk Fki mo (

(по свойству внутренних сил).

Fki ) 0

Итак,

dK z

mo (

mz (

(3.44 );

(3.45 )

Fke );

Fke ).

Производная по времени от кинетического момента системы относительно центра равна сумме моментов, действующих на систему, внешних сил, относительно этого же центра.

5.4 Законы сохранения кинетического момента

Рассмотрим два частных случая

1) Если mo (Fke ) 0, то ddtKo 0 и Ko const Ko / o .

(закон сохранения кинетического момента системы относительно центра).

2) В случае, когда mz (Fke ) 0, получаем dKdtz 0 и K z const K zo / o . (закон сохранения кинетического момента системы относительно оси)

5.5Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси

Из теоремы об изменении кинетического момента (3.45) получим дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси. После подстановки (3.43) в (3.45) будем иметь

I z	d	mz (Fk		) или I z mz (Fk		) , (3.46);	(3.47 )
	d		e		e
	dt
	dt

			131
	d 2	d	- угловое ускорение тела; угол его поворота.
где	dt 2	dt	- угловое ускорение тела; угол его поворота.

Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси аналогично дифференциальному уравнению поступательного движения тела в проекциях на какую либо ось, например на ось Ох. В уравнение (3.47) вместо координаты х входит угол поворота , а вместо массы тела М – момент инерции Iz относительно оси вращения Oz, вместо Fkxe входит mz (Fke ) - вращательный момент внешних сил.

Когда mz (Fke ) const , тело вращается с постоянным ускорением

mz (Fke )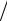I z .

Если mz (Fke ) 0, то d 0 и const (случай dt

равномерного вращения тела по инерции).

5.6 Дифференциальное уравнение плоскопараллельного движения твердого тела

Представим плоскопараллельное движение тела в виде совокупности двух движений – поступательного вместе с полюсом (центром масс тела С) и вращательного вокруг оси, проходящей через полюс перпендикулярно плоскости движения тела.

Воспользуемся теоремами о движении центра масс и изменении кинетического момента системы относительно центра масс для относительного движения системы.

Заметим, что теорема об изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе координат, движущейся поступательно с центром масс, формулируется так же, как если бы центр масс был неподвижной точкой.

132

На основании указанных выше теорем получаем дифференциальные уравнения плоскопараллельного движения твердого тела (в плоскости Оху),


Mxс	Fkx ;					(3.48)
		e
Myс Fky ;						(3.49)
			e
I zc mzс (Fk					) .	(3.50)
				e

где I zс - момент инерции тела относительно оси Сz.

Уравнения (3.48) и (3.49) описывают поступательную часть плоскопараллельного движения твердого тела вместе с полюсом – центром масс тела С. Уравнение (3.50) описывает вращательную часть плоскопараллельного движения твердого тела вокруг оси Сz, проходящей через центр масс тела С перпендикулярно плоскости движения тела.

133

Глава 6. Принцип Даламбера

6.1.Предварительные замечания

Принцип Даламбера является одним из важнейших общих принципов динамики несвободных материальных систем, имеющим обширное применение в практических вопросах.

Динамика, основы которой были заложены Ньютоном, рассматривала только свободные материальные точки и системы. По существу это была «небесная», а не «земная» динамика. Для развития техники, особенно для расчета механизмов и машин необходимо было разработать динамику несвободных материальных систем. Без знания именно такой динамики невозможно найти усилия, действующие во всех звеньях и узлах машины, чтобы затем провести их расчет на прочность.

Аксиом Ньютона недостаточно для решения задач несвободной системы – для этого необходимо ввести дополнительно некоторое положение физического характера. Таким дополнительным положением является принцип освобождаемости от связей, который был изложен ранее .

6.2.Принцип Даламбера для материальной точки и материальной системы

Введем следующее определение. Положением мгновенного динамического равновесия движущейся материальной точки называется такое положение, которое она занимает в настоящий момент времени по отношению к выбранной системе координат.

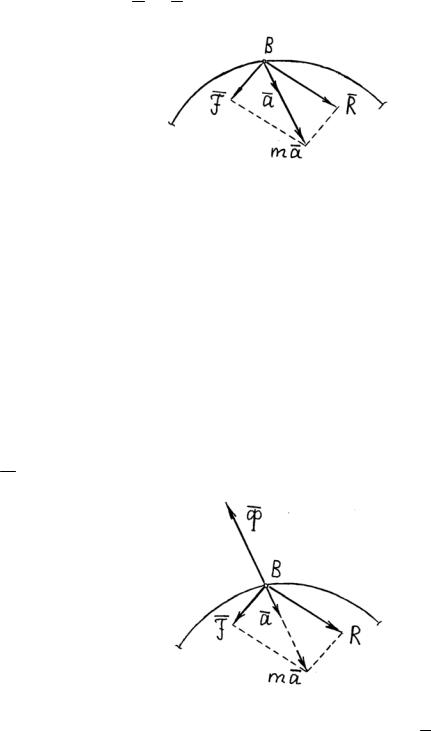
Для несвободной материальной точки второй закон Ньютона, называемый

законом движения имеет вид (рис. 3.16)
ma F R ,	(3.51)

где m – масса точки; а – ее ускорение; F – равнодействующая активных сил; R – равнодействующая реакций связей.

134

Заметим, что вектор ma (количество ускорения точки) представляет собой равнодействующую сил F и R .

Рис.3.16

В любой момент времени точка находится в положении мгновенного динамического равновесия под действием приложенных к ней сил (наблюдаемый факт «элемента покоя» точки). Условием этого равновесия точки будет равенство приложенных к точке сил

(3.52)

- неизвестная уравновешивающая сила.

где Т

С учетом (3.51) и (3.52) получаем рис.3.17

(3.53)

(F R ) ( та) Ф ,

где Ф – сила инерции точки.

Рис.3.17

Приходим к выводу, что уравновешивающая сила где Т представляет силу инерции точки и приложена к точке.

Дадим следующую формулировку принципа Даламбера, вытекающую из указанного выше факта мгновенного динамического равновесия точки.

Материальная точка в любой момент времени находится в положении мгновенного динамического равновесия при действии на нее

F R Ф 0 ,

135

уравновешенной системы сил, состоящей из активных сил, реакций связей и силы инерции точки

(3.54)

или F , R,Ф 0 ( в любой момент времени). (3.54') Главную роль в механике Ньютона играет закон движения, а два других

закона логически связаны с ним. Закон инерции непосредственно вытекает из закона движения.

После введения сил инерции можно установить, что из принципа Даламбера непосредственно вытекает обобщенный закон о действии и противодействии для движущейся несвободной точки, так как

Ф (F R ) Т .

Сила инерции Ф есть противодействующая сила по отношению к равнодействующей Т ускоряющих сил F и R .

Связью точки с телами, сообщающими ей ускорение, является материя (масса) точки (и окружающее пространство в случае неконтактных связей). Сила инерции точки создается действием на точку других тел (в виде ускоряющих сил F и R ), в результате которого возникает ее ускорение и противодействие – сила инерции Ф , как реакция количества материи (массы) на действие этих сил и сообщения точке неинерциального движения.

Таким образом, в создании силы инерции точки принимают участие все взаимодействующие с нею тела и материя (масса) самой точки.

Источником возникновения силы инерции являются сама точка и взаимодействующие с нею тела, как участники единого процесса действия противодействия.

Сила инерции, как и сила тяготения, относится к массовым силам. Эта сила приложена к самой точке и передается внешним связям, то-есть телам, сообщающим точке ускорение.

136

Все задачи динамики, которые можно решить при помощи принципа Даламбера, можно решать и не прибегая к помощи этого принципа. Однако он в высшей степени удобен и полезен при решении задач прикладного характера.

Для системы, состоящей из n точек, равенство (3.54), выражающее принцип Даламбера для точки, можно записать для каждой точки в виде

FК RК ФК 0 ; к = 1, 2, …, n (3.55)

Совокупность формул (3.55) выражает принцип Даламбера для системы.

6.3.Следствия из принципа Даламбера для материальной системы

Для решения задач применяют не сам принцип Даламбера, а его следствия. На основании этого принципа составим уравновешенную в любой момент

времени систему сил

F1 , F2 ,..., Fn ; R1 , R2 ,..., Rn ; Ф1 ,Ф2 ,...,Фn 0 .

Для плоской системы сил имеем следующие уравнения

FKX RKX ФКХ 0;
FKУ RKУ ФКУ 0;		(3.56)
mo (
mo (	FK ) mo (RK ) mo (ФК ) 0.

Полученные уравнения представляют собой следствия из принципа Даламбера для системы. Эти уравнения можно рассматривать, во-первых, как условия равновесия приложенных к точкам системы сил и сил инерции в любой

момент времени и, во-вторых, как условия мгновенного динамического равновесия системы в данный момент времени.

Особенностью уравнений (3.56) является отсутствие в них внутренних сил, что делает их особенно удобными при решении многих задач динамики.

Принцип Даламбера позволяет уравнениям динамики придать форму уравнений статики.

137

6.4.Приведение сил инерции точек твердого тела к простейшему виду

а)Главный вектор сил инерции точек тела Вычислим главный вектор сил инерции точек тела при любом движении тела

d 2

MrC M

d 2

R Ф ФК тК аК тК

dt 2K

dtC MaC ,

dt 2

где aK

d 2

; aC

d 2

и mK

rK MrC .

Главный вектор сил инерции точек тела равен силе инерции центра масс при условии, что в центре масс сосредоточена вся масса тела.

б)Поступательное движение тела При поступательном движении тела ускорения всех его точек равны

ускорению центра масс

а1 а2 ... аn a aC .
Силы инерции точек тела
	Ф1 т1а1 , Ф2 т2 а2 , …,	Фn тn аn образуют

систему параллельных связанных сил. При повороте этих сил вокруг их точек приложения вертикально вниз и умножением на величину g/а, получим вместо сил инерции силы тяжести точек (частиц) тела.

Силы инерции точек тела при поступательном движении приводятся к равнодействующей силе инерции, приложенной в центре масс тела и равной по величине произведению массы тела на ускорение центра масс

RCФ МаС .

в)Вращательное движение тела

Пусть однородное тело в виде пластинки, имеющее ось симметрии Оz, вращается вокруг этой оси (рис. 3.18).

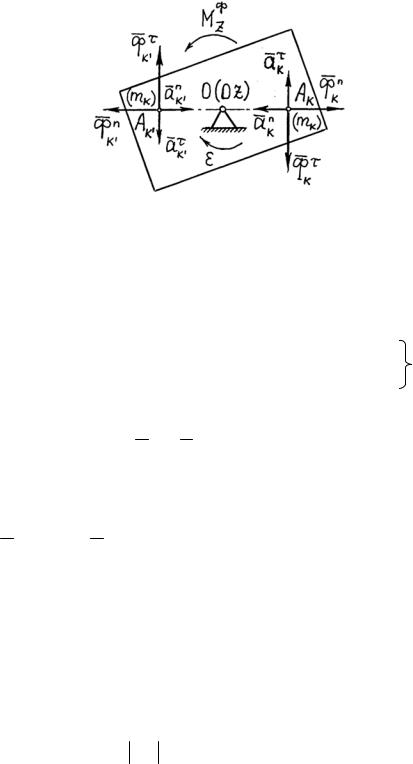
138

Рис.3.18

Возьмем две точки АК (mК) и АК' (mК), расположенные симметрично по отношению к оси вращения на расстояние ρК от этой оси. Будем считать, что тело состоит из пар таких точек. Силы инерции этих точек определяются по формулам

ФК тК аК тК К ФК ;		аК К ;
ФКn тК аКn	тК 2 К ФКn ;	аКn 2 К .
	к = 1, 2, …, n.

Касательные силы инерции ФК и ФК образуют пару сил.

Вычислим главный момент сил инерции точек тела относительно оси вращения Оz

МZФ тZ (ФК ) тZ (ФK ) тК К К тК К2 I Z ,

где I Z mK K2 – момент инерции тела относительно оси Оz; ε – угловая скорость тела.

Силы инерции точек тела приводятся к равнодействующей паре сил, момент которой равен произведению момента инерции тела относительно оси вращения на угловое ускорение тела

МZФ I Z ; МZФ I Z .

Момент МZФ изображается в виде круговой стрелки (рис. 3.19).

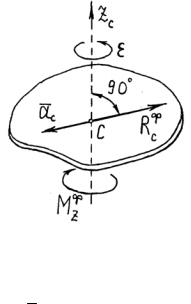
139

Рис.3.19

Заметим, что главный вектор сил инерции тела равен нулю, так как центр масс тела лежит на оси вращения RCФ 0 .

г)Плоско – параллельное движение тела Плоско – параллельное движение тела можно представить состоящим из двух

движений – поступательного вместе с некоторой точкой, принятой за полюс, и вращательного вокруг оси, проходящей через полюс и перпендикулярной к плоскости движения тела.

Будем считать тело однородной пластинкой. Примем за полюс С центр масс тела (рис. 3.19).

В данном случае получаем

			(
			(	Ф1 ,Ф2 ,...,Фn ) ~ (	R	CФ , M ZФC ),
где		CФ MaC	– главный вектор сил инерции точек тела; МZФC I ZC –
где	R	CФ MaC	– главный вектор сил инерции точек тела; МZФC I ZC –

главный момент сил инерции точек тела относительно оси ZС (рис. 3.19).

При плоско – параллельном движении силы инерции точек тела приводятся к силе и паре сил; сила равна главному вектору системы сил и приложена в центре масс тела; момент пары равен главному моменту сил инерции точек тела относительно оси, проходящей через центр масс перпендикулярно плоскости движения тела.

140

Глава 7. Принцип возможных перемещений

7.1.Предварительные замечания Главы 7 и 8 содержат элементы аналитической динамики и аналитической

статики.

Методы аналитической механики плодотворны как в теоретических исследованиях, так и в практических расчетах самых разнообразных машин и механизмов.

Аналитическая механика изучает движение и равновесие материальных систем с помощью некоторых основных начал (принципов). В ней влияние связей на движение систем учитывается не только мысленным освобождением от них, но и рассмотрением тех перемещений, которые допускаются наложенными на систему связями.

Аналитическая механика пользуется только одним аппаратом – вычислением работы.

7.2 Связи и их классификация Материальная система называется свободной, если координаты и скорости ее

точек могут принимать произвольные значения. В противном случае материальная система является не свободной. Ограничения, накладываемые на координаты и скорости точек системы, называются связями. Представим общий вид уравнения связи

f (x1 , y1 , z1 ,..., xn , yn , zn , x1 , y1 , z1 , , xn , yn , zn ;t) 0, .

где x1, y1, z1 ,...- координаты точек системы; x1, y1, z1 ,... – проекции скоростей этих точек.

Связи называются стационарными, если в их уравнения время явно не входит. В противном случае связи являются стационарными.

Связи называются удерживающими, если для любого перемещения точки можно указать и противоположное ему перемещение. В противном случае связь называется неудерживающей.

141

Связи называются геометрическими (голономными), если их уравнения могут быть представлены в виде, не содержащем производных от координат точек по времени. В противном случае связи являются кинематическими (голономными). Уравнения таких связей кроме координат содержат и их производные по времени.

7.3 Обобщенные координаты. Число степеней свободы системы

Пусть мы имеем материальную систему состоящую из n точек и подчиненную p стационарным, удерживающим и геометрическим связям вида

f j (x1 , y1 , z1 ,..., xn , yn , zn ) 0;

j 1,2,..., p .

(3.57)

Если бы система была свободной, то все 3n декартовых координат ее точек были бы независимыми. В нашем случае система имеет N=(3n-p) независимых координат.

Число независимых координат точек системы называют числом степеней ее свободы.

Если задать произвольно N декартовых координат, то остальные p координат можно найти из p уравнений связей (3.57). Однако такой способ выбора независимых координат часто приводит к сложным зависимостям. Удобнее ввести N каких-либо независимых между собой геометрических параметров q1 , q2 , q3 ,…, qN (они называются обобщенными координатами), которые однозначно определяют положение системы в пространстве. Заметим при этом, что число обобщенных координат равно числу степеней свободы системы. В качестве обобщенных координат обычно выступают линейные и угловые размеры, площади и объемы.

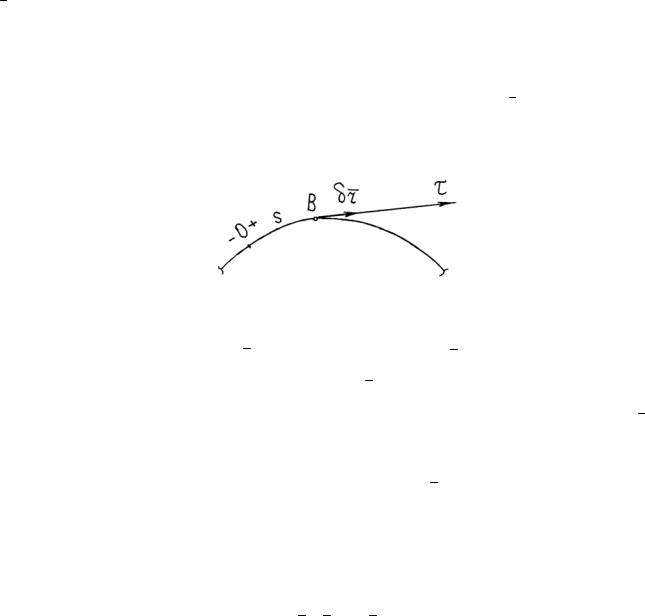
142

7.4 Возможные перемещения точки и системы

Возможным перемещением точки называется воображаемое (мысленное) бесконечно малое перемещение, допускаемое в данный момент времени наложенными на точку связями.

Для возможного перемещения точки не требуется времени для его совершения в отличие от действительного (элементарного) перемещения точки dr , которое точка совершает за время dt под действием приложенных сил при заданных начальных условиях и наложенных связях.

На рис. 3.20 показан участок кинематически возможной (допускаемой связями) траектории точки. Возможное перемещение точки r направлено по касательной к указанной траектории.

Рис.3.20

Возможное перемещение r , как и действительное dr , являются векторами.

Проекции	возможного	перемещения		r	на	оси координат (вариации
координат) обозначают х,		у, z , а проекции действительного перемещения dr
(дифференциалы координат) обозначают dх, dу, dz.
Величина	возможного	перемещения	точки				r	s , где	s OB – ее

криволинейная координата.

Возможным перемещением системы называется совокупность возможных перемещений всех ее точек

r1 , r2 ,..., rn .

В качестве примера рассмотрим кривошипно-шатунный механизм, размеры звеньев которого известны, а положение задано при помощи угла φ (рис. 3.21).

143

Рис.3.21

Мысленно сообщим кривошипу ОА возможное угловое перемещение δφОА (рис. 3.21б). Точки А и В получат возможные перемещения rA и rB ; шатун АВ – возможное вращательное перемещение δφАВ вокруг точки РАВ.

Возможные перемещения звеньев ОА и АВ направлены так же, как и угловые скорости этих звеньев ωОА и ωАВ; возможные перемещения rA , rB точек А и В направлены так же, как и их скорости VA , VB в том случае, если бы механизм пришел в движение. Точка РАВ, которая является возможным центром поворота звена АВ, совпадает с мгновенным центром скоростей этого звена.

Из зависимостей

;

APAB

CPAB

sB BPAB AB ;

CPAB AB

вытекает, что возможные перемещения всех точек механизма могут быть выражены через одно возможное перемещение Механизм имеет одну степень свободы.

7.5 Возможная работа силы. Идеальные и неидеальные связи Введем понятие о возможной работе силы. Мысленно сообщим точке

приложения силы F возможное перемещение r (рис.3.22).

144

Рис.3.22

Возможной работой силы называется работа, выполняемая силой на

возможном перемещении точки ее приложения

(3.58)

Возможная работа силы равна скалярному произведению силы на возможное

перемещение точки ее приложения.

На основании (3.58) получаем (Fz = 0)

F s ,

где F F cos

F cos ;

s ;

s OB ;

F - величина касательной составляющей силы

; s - криволинейная

координата точки В; s - величина вектора

А F Fx x Fy y Fz z;

(Fx , Fy , Fz );

( x, y, z), (3.59)

где x, y, z – координаты точки В;

x, у, z – приращения (вариации) координат этой точки.

Связи называются идеальными, если сумма возможных работ их реакций равна нулю.

Условие идеальности связей имеет вид

n
A(Rk ) RK rK ,	(3.60)

k 1

145

где RK – реакция связи, приложенная к к-ой точке системы; rK – возможное перемещение этой точки.

Если условие (3.60) не выполняется, связи называются неидеальными. В абсолютно твердом теле все точки связаны идеальными связями. Другими примерами идеальных связей являются абсолютно гладкая поверхность или плоскость, абсолютно гладкие шарниры; гибкие нерастяжимые связи типа нитей, канатов, тросов; закрепленные (неподвижные) точки тела.

7.6 Обобщенные силы и их вычисление

Рассмотрим материальную систему, подчиненную идеальным, стационарным, удерживающим и геометрическим связям, состоящую из n точек и находящуюся под действием активных сил (F1 , F2 ,..., Fn ) . Данная система имеет N степеней свободы, причем N=3n-p.

Положение системы в пространстве определяется N обобщенными координатами (q1 ,q2 ,...,qn ) .

Сообщим системе возможные перемещения ( r1 , r2 ,..., rn ) и вычислим сумму возможных работ всех активных сил. В результате получим

Aкакт

Qiакт qi ,

(3.61)

k 1

где q1 ,q2 ,...,qN - приращения (вариации) обобщенных координат;

(

акт ,

акт

,...,

акт )

- обобщенные силы при соответствующих обобщенных

координатах.

Обобщенной силой, соответствующей некоторой обобщенной координате, называется коэффициент при приращении этой обобщенной координате в выражении для суммы возможных работ всех активных сил системы.

Рассмотрим наиболее удобный способ вычисления обобщенных сил. Сообщим системе такое возможное перемещение, при котором приращение

всех обобщенных координат, кроме одной, равны нулю. Это означает, что у

146

системы мысленно отнимаются все степени свободы, кроме одной. Коэффициент при ненулевом приращении обобщенной координаты в выражении для суммы возможных работ всех активных сил системы дает нам искомую обобщенную силу.

Пусть q j 0	, а все остальные qi 0				(i j) . Тогда
			Aкактj	Qактj	q j , откуда
акт		Aкактj	; ( j 1,2, , N ).,			(3.62)
Qj		q j	; ( j 1,2, , N ).,			(3.62)
		q j

По этой формуле последовательно вычисляются все обобщенные силы системы.

7.7 .Принцип возможных перемещений

Этот принцип содержит необходимые и достаточные условия равновесия материальных систем.

Для равновесия материальной системы с идеальными, стационарными , удерживающими и геометрическими связями необходимо и достаточно, чтобы сумма возможных работ всех активных сил была равна нулю и скорости всех точек системы в начальный момент времени были равны нулю.

Aкакт 0				k 1,2, ,n ,
	Vk		(0) 0;

Докажем необходимость.

Пусть система находится в равновесии, тогда для каждой точки выполняются условия

(3.63)

Rk 0;

Сообщим системе возможное перемещение. Умножим (3.63) скалярно на

rK ,

и сложим все уравнения

(3.64)

rk 0 .

147

Ввиду идеальности связей Rk rk 0.

При равновесии системы должно выполнятся равенство, называемое общим

уравнением статики
Fk rK 0 или	Акакт 0.	(3.65), (3.65 )

Докажем достаточность. Предположим, что условие (3.65) выполняется, но система пришла в движение. В данном случае действительные перемещения совпадают с возможными drk rkв (связи стационарные). На основании теоремы об изменении кинетической энергии

Fk drk Rk drk dT 0 ,

где dT - значение дифференциала кинетической энергии системы.

Так как Rk drk Rk rk =0, то Fk drk Fk rk 0, что несовместимо с принятым предположением. Отсюда следует, что система находится в равновесии.

Глубокое содержание принципа возможных перемещений выражается при помощи общего уравнения статики. Приведем различные формы этого уравнения

n				n		n
		rk	0 ;	Fk sk	0 ;	(Fkx xk	Fky yk	Fkz zk ) 0.	(3.65 )
	Fk
к 1				к 1		к 1

7.8 Общее уравнение статики в обобщенных силах Переходя от (3.65) к обобщенным силам, получим

N
Qiакт qi 0;	i 1,2, , N ,

i 1

Всилу независимости приращений обобщенных координат получаем

Qакт 0;	i 1,2, , N	(3.66)
i

148

Уравнения (3.66) представляют собой условия равновесия системы, выраженные в обобщенных силах. Число условий равновесия системы равно числу степеней ее свободы.

Итак, для равновесия системы необходимо и достаточно, чтобы обобщенные активные силы при выбранных обобщенных координатах были равны нулю.

Глава 8 Общее уравнение динамики. Уравнение Лагранжа 2-го рода

8.1 Общее уравнение динамики

Пусть мы имеем материальную систему, состоящую из n точек. Применим к каждой точке системы принцип Даламбера для точки

		к = 1, 2, …, n (3.67)
	FK RK ФК 0 ;
Принцип Даламбера выражает		условие мгновенного динамического

равновесия системы (3.67) под действием приложенной уравновешенной системы сил FK , RK ,ФК . Применим к каждой точке принцип возможных перемещений и просуммируем все полученные уравнения

(

к = 1, 2, …, n.

(3.68)

FK RK ФК )

rK 0;

Просуммируем равенства (3.68) по всем точкам системы

(3.69)

rK RK

rK ФК

rK 0 .

Ввиду идеальности связей окончательно получаем

(3.70)

rK ФК

rK 0 ,

или АКАКТ АКИН 0 ,

(3.71)

где

активных сил

и сила инерции,

FK и ФК – равнодействующая

приложенные к к-ой точке системы; rK – возможное перемещение этой точки,

АКАКТ FK rK – сумма возможных работ активных сил,

АКИН ФK rK – сумма возможных работ сил инерции точек системы.

Уравнение (3.71) называется общим уравнением динамики или объединенным принципом Даламбера – Лагранжа.

149

При движении материальной системы с идеальными связями сумма возможных работ всех активных сил и сил инерции точек системы равна нулю в любой момент времени

Приведем эквивалентные формы общего уравнения динамики (3.71) (примем

Fкz = 0; Фкz = 0)

FKX ФКХ	xK FКУ ФКУ yK 0 .	(3.71')
FKX mk xk	xK FКУ mk yk yK 0 .	(3.71' )

где xK , yK , zК - координаты k -ой точки системы;

xK , yK , zК - проекции ускорения этой точки на оси координат.

Общее уравнение динамики дает полную информацию о движении системы с помощью соответствующей системы дифференциальных уравнений.

8.2 Общее уравнение динамики в обобщенных координатах. Принцип Даламбера для материальной системы, выраженный в обобщенных силах

Воспользуемся понятием обобщенных сил (3.66)

rK Qiакт qi ,

rK Qiин qi ,

k 1

где q1 ,q2 ,...,qN

- приращения (вариации) обобщенных координат;

(

акт ,

акт

,...,

акт ) ,

(

ин ,

ин

,...,

ин )

обобщенные активные силы и

обобщенные силы инерции при соответствующих обобщенных координатах. Общее уравнение динамики в обобщенных координатах имеет вид

(Qiакт Qiин ) qi	0 ;	i = 1, 2, …, N. (3.72)
Ввиду независимости обобщенных координат получаем
Qакт Qин 0 ;		(3.73)
i	i

Условие (3.73) называется принципом Даламбера для системы, выраженным в обобщенных силах.

150

При любом движении материальной системы суммы обобщенных активных сил и сил инерции точек системы равны нулю для каждой обобщенной координаты в любой момент времени.

При использовании общего уравнения динамики необходимо уметь вычислять возможную работу сил инерции точек системы.

8.3 Уравнение Лагранжа 2-го рода

Придадим общим уравнениям динамики в обобщенных силах вид, полученный Лагранжем.

Непосредственное вычисление обобщенных сил инерции во многих случаях вызывает затруднения. Между тем кинетическая энергия системы легко вычисляется. Отсюда возникает идея – выразить обобщенные силы инерции через кинетическую энергию системы.

С этой целью преобразуется выражение для обобщенной силы инерции Qiин , соответствующей обобщенной координате qi . В результате преобразований приходим к выражению

ин

(3.74)

После подстановки (3.73) в (3.74) получаем уравнения Лагранжа 2-го рода

АКТ

;

i = 1, 2, …, N,

(3.75)

где Т – кинетическая энергия системы;

qi - обобщенные координаты; qi -

обобщенные скорости;

Q АКТ - обобщенная сила при выбранной обобщенной

координате qi ; N - число степеней свободы системы.

Уравнения Лагранжа представляют собой дифференциальные уравнения движения в обобщенных координатах. Они являются обыкновенными дифференциальными уравнениями 2-го порядка, как и дифференциальные

151

уравнения движения точки в декартовых координатах. Преимущества уравнений Лагранжа заключается в следующем:

1.Для удобства и простоты описания движения системы вместо декартовых координат в качестве независимых координат используются связанные с ними величины, называемые обобщенными координатами.

2.Силы, действующие на систему, представляются в виде обобщенных сил, в которых реакции идеальных связей не учитываются.

3.Использование выражения для кинетической энергии системы - положительной скалярной величины, которая легко вычисляется.

4.Число уравнений не зависит от числа входящих в систему материальных точек или тел, и равно числу степеней свободы системы.

5.Эти уравнения дают единый и притом достаточно простой метод решения задач для любых систем, как угодно движущихся.

8.4Методика применения уравнений Лагранжа 2-го рода к составлению и интегрированию дифференциальных уравнений движения материальной системы

1.Изобразить систему в произвольной момент времени. Приложить к точкам системы заданные (активные) силы. Силы трения следует отнести к активным силам.

2.Определить число степеней свободы и выбрать обобщенные координаты.

3.Вычислить кинетическую энергию системы и выразить ее через обобщенные координаты и обобщенные скорости.

4.Найти обобщенные силы системы, соответствующие выбранным обобщенным координатам.

5.Выполнить математические операции, предусмотренные уравнениями Лагранжа 2-го рода.

6.Указать начальные условия (начальные значения обобщенных координат и обобщенных скоростей).

152

7. Проинтегрировать составленные уравнения Лагранжа 2-го рода.

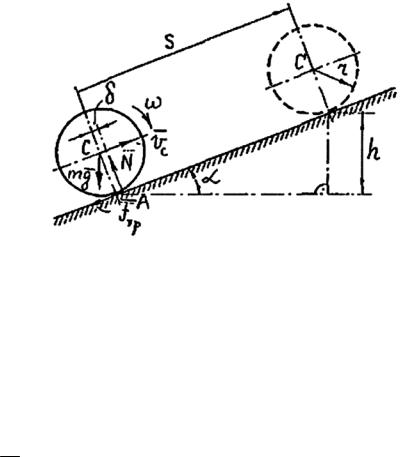
153

Глава 9. Решение задач по динамике

Задача 3.1 (рис.3.23)

. Какую начальную скорость, параллельную линии наибольшего ската наклонной плоскости, надо сообщить оси колеса радиуса r , чтобы оно, катясь без проскальзывания, поднялось на высоту h по наклонной плоскости, образующей угол с горизонтом ? Коэффициент трения качения равен . Колесо считать однородным диском. Определить также ускорение оси колеса.

Решение. (рис.3.23)

Воспользуемся теоремой об изменении кинетической энергии.

T T0 Ake .

i 1

	(рис.3.23)
Кинетическая энергия колеса в начальном положении
T 0	mV	2	J	2	3mV 2
	c		c		c .
	2		2		c .
	2		2		4
Собственный момент инерции колеса равен Jc						1 mr 2	и его угловая
						2

скорость Vrc ,

На колесо действует сила: тяжести mg , нормальная реакция плоскости N mg cos , трение скольжения Fтр и момент трения качения M тр N .

154

Вычислим работу активных сил, приложенных к колесу (угол поворота колеса rs )

Ak mgs sin (N ) mgs sin

cos .

k 1

На основании указанной теоремы имеем

mVc

mV0

mgs sin

cos .

В верхнем положении колесо остановится,

следовательно, Vc 0 и

перемещение оси колеса составит s

. Скорость оси колеса в начальном

sin

положении в функции высоты подъема h

VС0

g 1

ctg h .

Дифференцируя по времени это выражение, получим

cos

g sin

Ускорение оси колеса (учитываем, что V ds )

sin

cos .

Задача 3.2 (рис.3.24)

По призме Е массой m 7 кг могут двигаться тележки А и В массами

m1 1кг и m2 2 кг соответственно . Тележки связаны тросом. В начальный момент времени система находилась в состоянии покоя, а затем тележка А начинает двигаться относительно призмы вправо под действием внутренних сил. Пренебрегая потерями на трение, определить перемещение призмы Е для момента времени t1 0.5с, если закон относительного движения тележек s 2t2 м.

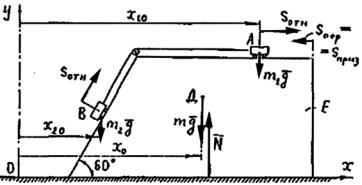
155

(рис.3.24)

Решение. (рис.3.24)

Система состоит из трех подвижных тел и все тела двигаются поступательно. На систему тел действуют силы тяжести mЕg , mАg и mВg , а также результирующая нормальной реакции поверхности N . Для решения используем теорему об изменении количества движения системы

dQx	nF		e		nF
dt		Fkx		;		e	Qx const 0
		Fkx		;		e
	i 1				Fkx 0;
					i 1

По условию задачи (все внешние силы вертикальны, вначале система неподвижна, призма Е перемещается по горизонтальной плоскости).

Qx M xc 0;	xc const xcv Выполняется закон сохранения проекции центра
масс системы на ось Ох
	3
		mk хk			3	3
	хc	k 1	хco	или	mk õk mk õkv
	хc	3	хco	или	mk õk mk õkv
		mk			k 1	k 1
					k 1	k 1

Спомощью этой зависимости составим выражение

m1 x10 m2 x20 m x0

îòí

ïåð

) m

îòí

cos60 s

ïåð

) m(x

ïåð

где sотн =2t2 –закон относительного движения тележки;

sпризм = sпер –переносное перемещение тележки (перемещение призмы) Окончательно находим

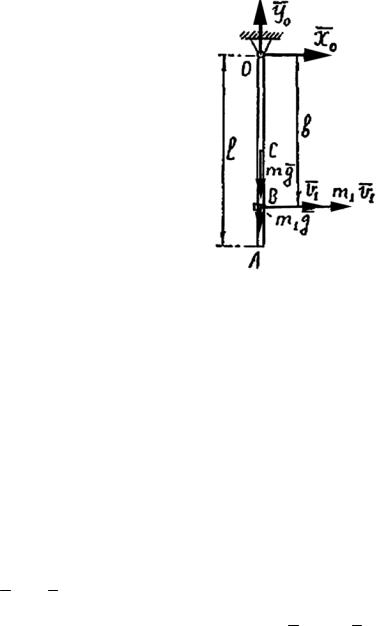
156

	m1 m2 cos60				sîòí м.
sïðèç m m		2	m
	1
При m 7 кг, m1 1кг и m2	2 кг, и t1 0.5с получим
sïðèç	1 2 0.5
		2t 2			0.1м.
	7 1 2			t 0.5

Задача 3.3 (рис.3.25)

(рис.3.25)

Доска ОА массой m =4кг и длиной l =1м может вращаться без трения вокруг горизонтальной оси О. В неподвижную доску на расстоянии b =0.8м от оси О попадает и застревает пуля массой m1=0.01кг, летевшая со скоростью V1 =800м/с. Определить угловую скорость доски после попадания пули. При вычислении момента инерции доску считать однородным стержнем.

Решение. (рис.3.26)

На доску действуют силы тяжести mg , а также составляющие реакций оси ХО и YО .рис.3.25. После попадания пули в доску действуют силы: mg m1 g а также составляющие реакций оси ХО и Y Î YО . рис.3.26.

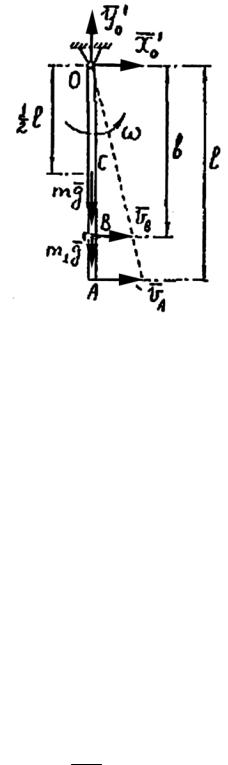
157

(рис. 3.26)

На основании теоремы об изменении кинетического момента имеем

dK z

;

mz Fk

K z

K z 0

const

Выполняется закон сохранения кинетического момента системы

относительно оси. В начальном положении доска неподвижна, поэтому

K zо

m1V1b .

После попадания пули в доску

Kz m1V1b J z (m1b2 ml 2 ),

где J z

ml 2

-момент инерции доски относительно оси Oz,

V b .

С помощью равенства m1V1b ml3 2 m1 b2

определяем угловую скорость доски

	3m1V1b	3 0.01	800 0.8	4.8 рад/с.
	ml 2 3m b2	4 12 3	0.01 0.82	4.8 рад/с.
1

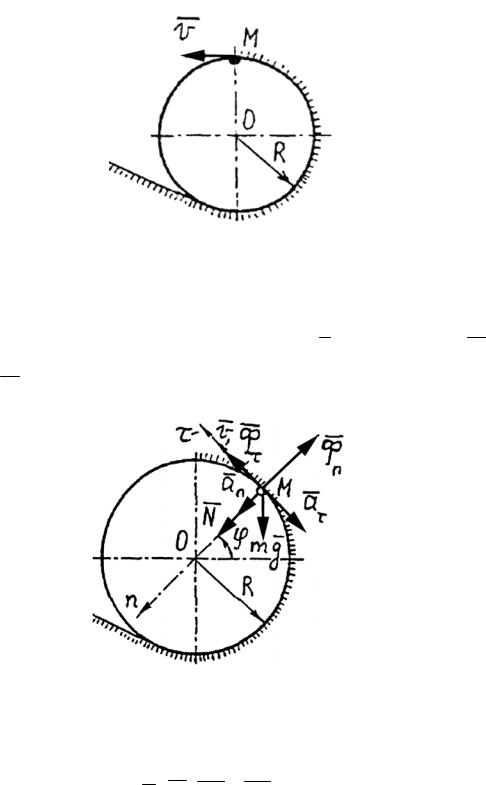
158

Задача 3.4 (рис.3.27), (рис. 3.28)

При каком минимальном значении скорости тяжелый шарик пройдет высшую точку петли радиуса R , не отрываясь от нее ? Петля расположена в вертикальной плоскости.

Решение. (рис.3.27)

Будем считать шарик материальной точкой. Рассмотрим положение шарика в промежуточном положении на его траектории. Приложим к шарику силы тяжести mg , нормальную реакцию петли N , касательную Ф и

нормальную Фn силы инерции.

(рис.3.28)

В соответствии с принципом Даламбера получаем уравновешенную в любой момент времени систему сил

( m g , N ,Ô ,Ô n ) 0 .

Проектируя эту систему сил на главную нормаль Mn, получим

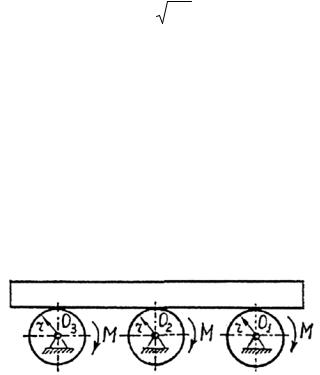
			159
		mg sin N Ôn 0,
где Фn = mаn,	an	mV 2	-нормальное ускорение шарика, V-скорость
		R

шарика.

По условию задачи при 90 нормальная реакция петли в ее верхней точке равна нулю, т.е. N 0 .

N Фn g sin 0;	sin sin 90 1;	mV 2	mg 0 .
		R
	Скорость шарика
	V	Rg .

Задача 3.5 (рис.3.29), (рис.3.30)

Три одинаковых ролика массой m1 и радиусом r каждый перемещают горизонтальную плиту массой m . Ко всем роликам приложены равные вращающие моменты M . Определить ускорение плиты при условии, что она движется по роликам без проскальзывания. Ролики считать сплошными однородными цилиндрами.

(рис.3.29)

Решение. (рис.3.30)

Для решения будем использовать общее уравнение динамики. Принимаем, что ускорение плиты равно a , а ее возможное перемещение

s . Тогда угловое ускорение каждого ролика ar , а его возможное угловое перемещение rs .

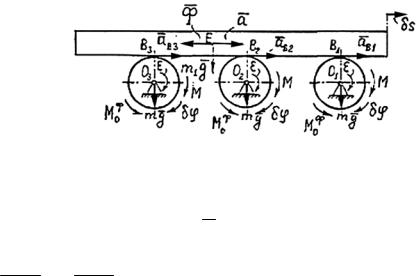
160

(рис.3.30)

К плите и роликам приложим силы тяжести mg и m1 g вращающие моменты M , силу инерции плиты Ф ma и моменты сил инерции роликов

M оф J m12r 2 ar m12ra .

Для данной системы общее уравнение динамики имеет вид

	Ф s 3( M M оф ) 0 ,
откуда	ma s 3( M						m1ra	)	s	0 .
откуда	ma s 3( M							)	r	0 .
					2				r
	3M			3m
	r	m		1	a .
	r			2
	Ускорение плиты
	a	6 M				.
	a	( 3m	2m )r			.
		1

Задача 3.6 (рис.3.31), (рис.3.32)

Для заданной составной конструкции определить реактивный момент в заделке А, считая заданными интенсивность равномерно распределенной нагрузки q , угол , длины стержней АВ= l1 и ВС= l2 .

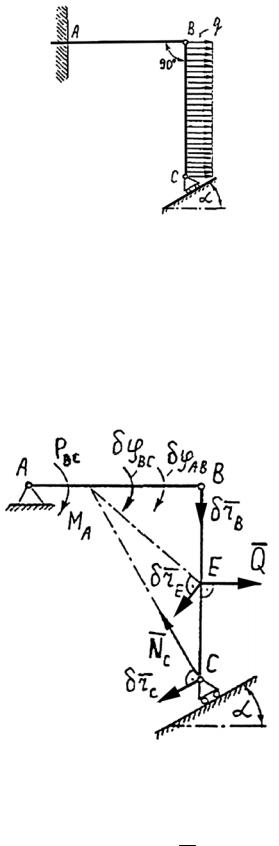
161

(рис.3.31)

Решение. (рис.3.32)

Для решения задачи используем принцип возможных перемещений. Заменим заделку в точке А шарнирно неподвижной опорой,

компенсировав отброшенную связь ее реакцией – реактивной парой сил с неизвестным моментом МА .

(рис.3.32)

Распределенную нагрузку на участке ВС заменим приложенной к точке Е равнодействующей силой Q ql2 (ВЕ=ЕС= l22 ).

Сообщим системе возможное перемещение, повернув стержень АВ на угол AB . Стержень ВС совершит возможное плоскопараллельное

162

перемещение, повернувшись на угол BС вокруг точки РВС . Точки В, С и Е получат соответствующие возможные перемещения

AB AB l1 AB ;

l1 AB ;

EPBC BC EPBC

l1 AB .

CPBC

BC CPBC

Уравнение возможных работ имеет вид

Ì À ÀÂ (Q BE) BC

Ì À (Q BE)

(Q BE) i

ÀÂ

Далее находим

i BC BC

ÀÂ SÂ

Окончательно получим

AB AB

ÀÂ

ÂC

ÀÂ

À (Q BE) i

ql2l1ctg .

Литература

1.Никитин Н.Н. Курс теоретической механики. – М.: Высшая школа, 1990. 2.Старжинский В.М. Теоретическая механика. – М.: Наука, 1980.

3.Тарг С.М. Краткий курс теоретической механики. – М.: Высшая школа, 1995.

4.Цывильский В.Л. Теоретическая механика. – М.: Высшая школа, 2001. 5.Капранов И.В. Теоретическая механика. Часть 1. Статика. – М.: РГОТУПС,

2001.

6.Капранов И.В. Теоретическая механика. Часть 2. Кинематика. – М.: РГОТУПС, 1992.

7.Капранов И.В., Федоринин Н.И., Алейников И.А. Принципы механики. – М.: РГОТУПС, 2002.

8.Капранов И.В., Федоринин Н.И. Принцип возможных перемещений. – М.: РГОТУПС, 2002.

9.Капранов И.В., и др.. Теоретическая механика. Уравнения Лагранжа 2-го рода.. – М.: РГОТУПС, 2007.

163

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1313

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.09.2019286.72 Кб13Лекции по налогам.doc
#
03.03.2016199.33 Кб41Лекции по ОЭТ.docx
#
05.09.201930.07 Кб18Лекции по птранспортному праву.docx
#
17.11.20183.23 Mб65Лекции по сетям и система.doc
#
19.08.2019831.5 Кб44Лекции по сорокиной.docx
#
03.03.20163.26 Mб381Лекции по Теоретической механике.pdf
#
01.03.2025179.2 Кб2Лекции по ФЖД(все).doc
#
01.04.2025792.58 Кб3Лекции по ФЖД.doc
#
20.08.2019338.66 Кб69лекции по физ.-ре 1,2 курсы, 1 семестр.docx
#
04.12.20181.82 Mб32Лекции по ФМ 2011 Б.doc
#
01.05.2025742.4 Кб2Лекции по ЭО для заочников перер и доп.doc