
- •И.В.Капранов, В.С.Дубровин
- •Лекции по теоретической механике
- •Учебное пособие для студентов
- •Курс лекций для студентов РОАТ технических специальностей разработали члены корреспонденты Международной Академии Наук Педагогического Образования
- •Глава 2.2. Простейшие движения твердого тела...................................................
- •Глава 2.3. Плоско – параллельное движение твердого тела..................................
- •Глава 2.4. Сложное движение точки......................................................................
- •Глава 2.5. Решение задач.по кинематике................................................................
- •Введение в динамику................................................................................................
- •Введение
- •Глава 2.2. Простейшие движения твердого тела
- •Глава 2.3. Плоско – параллельное движение твердого тела
- •Возьмем за полюс точку А
- •Скорость точки В
- •Глава 2.4. Сложное движение точки
- •Ускорение Кориолиса определяется по формуле
- •Даны уравнения движения точки
- •Задача 2.2
- •Решение
- •Задача 2.3
- •Решение
- •Скорость, касательное и нормальное ускорение точки
- •Решение
- •Задача 2.5
- •Задача 2.6
- •Решение
- •Решение
- •Скорость точки А кривошипа ОА
- •Введение в динамику
93
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
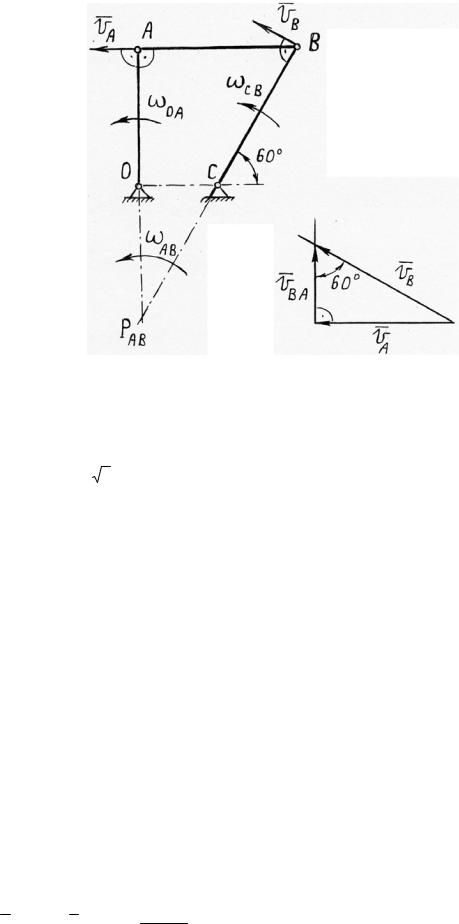
Рис. 2.29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
Скорость точки А кривошипа ОА |
||
VA OAOA 4 10 |
|
|
|
||||||||||||
3 69,2 [см/с]; VA OA |
|||||||||||||||
Взяв точку А за полюс, составим векторное уравнение |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
VB VA VBA , |
|
|
|
|
|||||||||||
где |
|
|
|
|
|
|
|
|
|||||||
VB CB и VBA BA . |
|||||||||||||||
На рис. 2.29 построено графическое решение этого уравнения (план |
|||||||||||||||
скоростей). |
|
|
|
|
|
|
|
||||||||
С помощью плана скоростей получаем |
|||||||||||||||
VB |
|
|
|
|
|
VA |
|
|
80 [см/с]; VBA VB sin 30 40 [см/с]. |
||||||
|
cos30 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
Угловая скорость шатуна АВ |
|||||||||||||||
AB |
|
VBA |
2 [с |
-1 |
]. |
|
|
||||||||
|
BA |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скорость точки В можно найти с помощью теоремы о проекциях скоростей двух точек тела на соединяющую их прямую (рис. 2.29)
ПрАВVB ПрАВVA ; VB cosV30A 80 [см/с].
94
В заключении найдем скорость точки В с помощью мгновенного центра скоростей РАВ шатуна АВ. Зная направления скоростей точек А и В (VА ОА и VB CB ) находим положение точки РАВ.
Угловая скорость шатуна АВ
АВ |
VA |
|
VA |
2 [с-1]. |
|
AP |
AB tg60 |
||||
|
|
|
Скорость точки В и угловая скорость кривошипа СВ
VB AB BPAB AB |
|
AB |
80 [см/с]; |
||||||
sin 30 |
|||||||||
|
|
|
|
|
|
|
|||
CB |
VB |
|
VB sin 60 |
4 [с |
-1 |
]. |
|||
CB |
OA |
|
|
||||||
|
|
|
|
|
|
|
|||
Задача 2.8
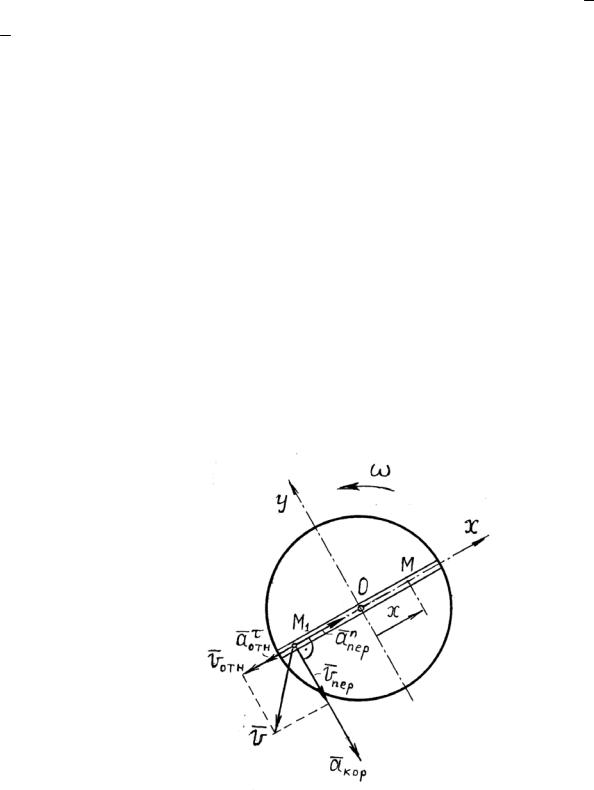
Вдоль прорези диска радиусом R = 10 [см] движется ползун М, расстояние которого от центра диска изменяется по закону ОМ = х = (10t – 3t2) [см]. Диск вращается с постоянной угловой скоростью ω = 2 [1/с] (рис. 2.30).
Рис. 2.30
Определить абсолютную скорость и абсолютное ускорение ползуна при t1 = 4 [с].
Решение

95
Движение точки (ползуна М) по прорези диска, считая диск неподвижным, является относительным. Движение точки М вместе с диском во вращательном движении является переносным.
Находим положение точки М на диске при t1 = 4[с].
ОМ1 = х1 = х(t1) = 10t1 – 3t12 = - 8[см].
Определяем абсолютную скорость точки М
V VOTH VПЕР .
VПЕР (t1 ) |
|
OM1 |
|
|
2 8 16 [см/с]; |
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6t ; |
VOTH (t1 ) 10 6t1 14 [см/с]. |
|||||||||||||
VOTH |
x |
|
10 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VOTH2 VПЕР2 |
21,26 [см/с]. |
||||||||||
V |
OTH |
VПЕР ; |
|
|
|
V |
|||||||||||||||||||
Найдем абсолютное ускорение точки М |
|||||||||||||||||||||||||
а аОТН |
|
аОТНn |
|
aПЕР |
аПЕРn |
aКОР ; |
|
|
|||||||||||||||||
аОТН |
х 6 [см/с2]; |
аОТНn |
|
VOTH2 |
|
0 |
|
||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aПЕР |
|
|
ОМ1 |
|
|
|
0 ; |
ε = 0 (ω = соnst); |
|
||||||||||||||||
|
|
|
|
||||||||||||||||||||||
аПЕРn |
2 |
|
ОМ1 |
|
22 8 32 [см/с2]. |
|
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
Ускорение Кориолиса |
|
|
|
|
|
|
|||||||||||||||||||
aКОР 2 VOTH
aКОР 2 VOTH sin ,^ VOTH 2 2 14sin 90 56 [см/с2].
Построим систему координат Оху (рис. 2.30). Вычислим проекции абсолютного ускорения точки М на эти оси координат в заданный момент времени t1
ах аОТН / х аПЕРn / х 6 32 26 [см/с2]
ау aКОР/ у 56 [см/с2].
Абсолютное ускорение точки М
а  ах2 ау2 61,74 [см/с2].
ах2 ау2 61,74 [см/с2].
96
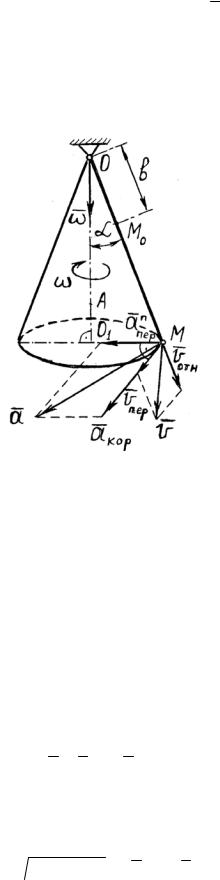
Задача 2.9 Точка М равномерно движется по образующей кругового конуса с осью ОА
от вершины к основанию с относительной скоростью VOTH ; угол МОА (рис. 2.31). В момент t0 = 0 расстояние ОМ0 = b. Конус равномерно вращается вокруг своей оси с угловой скоростью ω.
Найти абсолютную скорость и абсолютное ускорение точки М.
Рис. 2.31
Решение Движение точки М по образующей конуса, считая конус неподвижным,
является относительным. Движение точки М вместе с конусом во вращательном движении является переносным.
Находим положение точки М на конце в момент времени t S = ОМ = b + Vотнt; ОМ0 = b;
О'М = ОМ·sinα = (b + Vотнt) sinα.
Абсолютная скорость точки М
V VOTH VПЕР .
Vотн – известно по условию задачи;
Vпер = ω О'М = ω (b + Vотн t) sinα.
V  VOTH2 VПЕР2 ; VOTH VПЕР .
VOTH2 VПЕР2 ; VOTH VПЕР .

97
Абсолютное ускорение точки М
а аОТН аОТНn aПЕР аПЕРn aКОР ;
аОТН |
|
dVOTH |
0 |
|
(Vотн = соnst); |
|||||
|
|
|
||||||||
|
|
dt |
|
|
|
|
||||
|
аОТНn |
|
VOTH2 |
|
0 |
; |
||||
|
|
|||||||||
|
|
|
|
|
|
ε = 0 (ω = соnst); |
||||
aПЕР О М 0 ; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
2 |
|
|
2 |
b VOTH t sin . |
|||||
аПЕР |
О М |
|
||||||||
Ускорение Кориолиса
aКОР 2 VOTH
aКОР 2 VOTH sin ,^ VOTH 2 VOTH sin .
а (аПЕРn |
)2 аКОР2 |
; аПЕРn aКОР . |
