§7. Приложения тройного интеграла

I Вычисление объёмов тел

.

Пример 1. Вычислить объём тела, ограниченного поверхностями ,,.

Решение. Тело, представляет собой полушар с конической выемкой. Проекция на плоскость – круг радиусас центром в начале координат, следовательно, координатаССК изменяется от 0 до. Проекция на плоскость– полукруг с вырезанным сектором (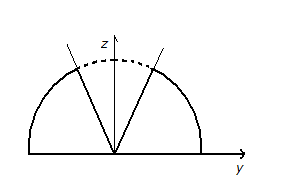сечение конусаэтой плоскостью – это). Координатаизменяется отна образующих конуса дона плоскости. И, наконец, координата.

Итак, объём тела

Здесь повторный интеграл представляет собой произведение трех интегралов, ибо внутренние интегралы не зависят от внешних переменных.

II Вычисление масс тел

где – плотность распределения массы.

Пример 2. Найти массу шара если плотность в каждой точкепропорциональна расстоянию отдо некоторой фиксированной точки поверхности шара.

Решение. Поместим фиксированную точку в начало координат, а центр шара на ось . Тогда уравнение сферы в сферических координатах имеет вид (см. §6, замечание 3):,. Далее, плотность,. Имеем для массы:

III Вычисление координат центра масс тела

Формулы для координат центра масс тела выводятся так же как аналогичные формулы для плоской фигуры. Не будем выводить их, а просто приведем:

П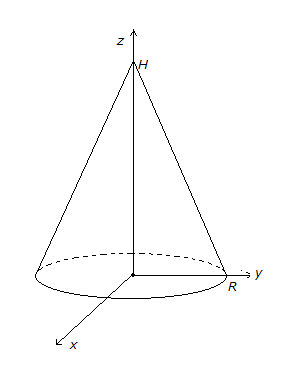ример 3. Найти положение центра масс однородного конуса с радиусом основания и высотой.

Решение. Расположим конус обычным образом: основание в плоскости , вершина на оси. Выясним какие поверхности ограничивают это тело. Одна из них – это плоскость, а вторая – это нижняя часть конической поверхности, смещенная вверх наН. Имеем:

Коэффициент найдем из того усло-вия, что пересечение этой поверхности с плоскостью– круг радиусаR:

.

Итак, задачу можно сформулировать так: «Найти координаты центра масс тела, ограниченного поверхностями и, если ». Тело симметрично относительно оси и в симметричных точках плотность одинакова. Следовательно, центр масс лежит на оси:

Итак, центр масс однородного конуса расположен на его оси на расстоянии четверти высоты от основания.

IV Вычисление моментов инерции тела

Формулы для всевозможных моментов инерции тела аналогичны подобным формулам для плоской фигуры.

Моменты инерции относительно осей координат:

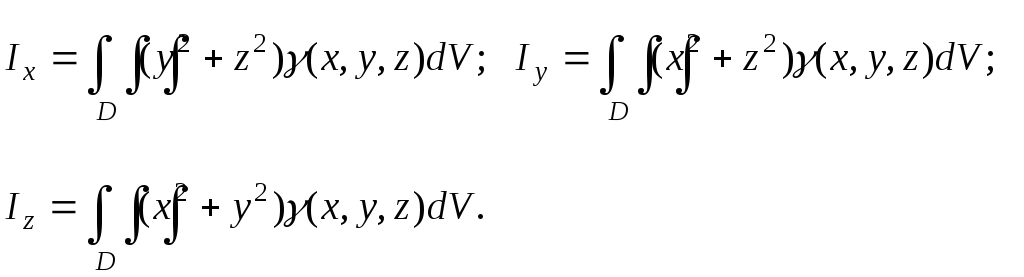
Моменты инерции относительно координатных плоскостей:

Момент инерции относительно начала координат:

Пример 4. Найти момент инерции цилиндра относительно фиксированной образующей, если плотность в каждой его точке обратно пропорциональна расстоянию от точки до этой образующей.

Р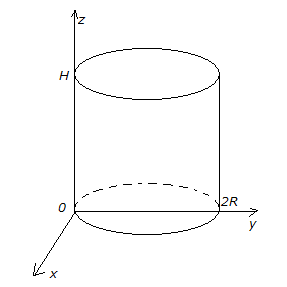ешение. Пусть образующая, о которой говорится в условии задачи, лежит на оси , а центр нижнего основания на оси. Цилиндр ограничен поверхностями

Цилиндрическое уравнение третьей поверхности: . Плотность

в силу условия Итак, момент инерции:

V Вычисление силы притяжения точки телом

Пусть в точке А находится масса , а в точкеВ – масса М. Известно, что М притягивает (и наоборот) с силойтакой, что, где).

Пусть теперь эти точки находятся в системе координат: Проекциисилывычисляются по формулам

Но поэтому, например,гдеАналогичные формулы есть дляи. Итак, проекции силы:

Пусть теперь тело имеет плотность. Как найти силу, с которой телопритягивает массу, находящуюся в точке? Можно поступить обычным, при построении приложений интеграла, способом. Всю областьразбиваем на части, выбираем точкии считаем, что вся массасосредоточена в. Получим системуматериальных точек:с массой. (Подобным образом мы поступали при вычислении координат центра масс и моментов инерции плоской фигуры. Так же можно поступить и при нахождении этих характеристик пространственной области.)

Точка притягиваетс силой, где, например,

вычисляются аналогично. Суммируя и переходя к пределу, получим для проекций полной силы :

где

Пример 5. Найти силу, с которой однородный конус притягивает массу, находящегося в его вершине.

Решение. Впишем данный конус в систему координат так, как показано на рисунке. Такой конус можно описать как тело, ограниченное поверхностями и(смотри пример 3).

В силу симметрии и однородности сила притяжения направлена по оси. Имеем:

.

Переходим к цилиндрическим координатам. Полярные координаты проекции произвольной точки тела на плоскость изменяются в пределах, а координатаизменяется от конуса до плоскости, т.е. отдо.

Итак,
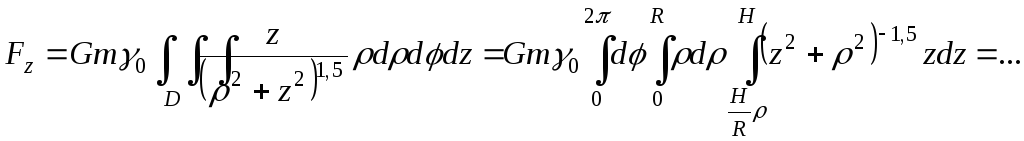