III Повторные интегралы в r2

Пусть функция непрерывна в правильной области . Зафиксируем и рассмотрим функцию одной переменной . Она непрерывна на отрезке , и поэтому интегрируема. Очевидно, интеграл от функции по данному отрезку является функцией от :

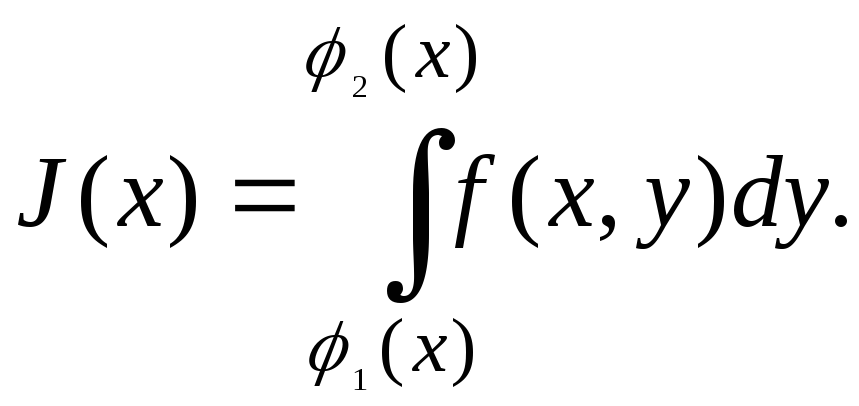
Если , то этот интеграл равен площади сечения цилиндрического тела (основание , «крыша» ). Можно доказать, что функция непрерывна на , а следовательно существует интеграл

Такая конструкция называется повторным интегралом от функции по области . Его принято обозначать несколько иначе:

(1)

Терминология очевидная: внутренний и внешний интегралы, внутренняя и внешняя переменные интегрирования. Заметим, что вычисления в (1) производятся справа налево.

Аналогично для области можно определить другой повторный интеграл

(2)

В повторном интеграле нет ничего нового по сравнению с определённым интегралом. Свойства его обычные: линейность, аддитивность. Смысл для – объём цилиндрического тела. Есть ещё одно свойство:

повторный интеграл не зависит от порядка интегрирования, т.е. интегралы (1) и (2) имеют равные значения.

Пример 7. Вычислить повторный интеграл от функции по области , ограниченной линиями , ,

Решение. Вся область лежит в полосе . Для каждого такого точки области лежат между осью и верхней половиной эллипса . Поэтому 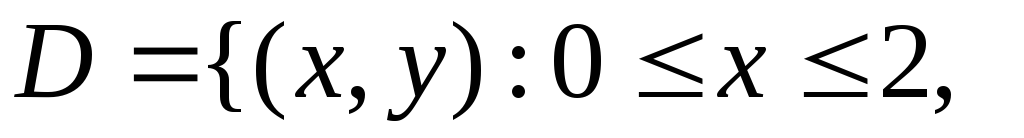и повторный интеграл имеет вид:

Предлагаем студентам самостоятельно использовать правильность области в направлении оси и вычислить повторный интеграл с другим порядком интегрирования.

Пример 8. Изменить порядок интегрирования в повторном интеграле

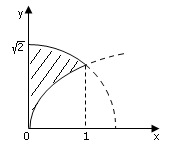Решение. Пределы интегрирования сразу дают нам уравнения линий, которые ограничивают область интегрирования. Левая и правая границы – это и , нижняя и верхняя – (ветвь параболы) и (верхняя полуокружность). Нарисуем эту область.

Вся область лежит в полосе . Левая граница – ось – задана одним уравнением . А правая граница состоит из двух частей: параболы и окружности. Разрешим уравнения этих границ относительно : ; (здесь перед радикалом берём знак «+», ибо по условию ). Точка пересечения этих кривых имеет ординату . Итак, имеем для области:

и для повторного интеграла:

IV Повторные интегралы в r3

Повторный интеграл в пространстве вводится аналогично повторному интегралу на плоскости.

Пусть функция непрерывна в правильной области , причём – правильная область в :

Зафиксируем точку и проинтегрируем непрерывную функцию –функцию одной переменной ! – по отрезку . Очевидно, что полученный интеграл будет зависеть от координат точки :

Можно показать, что функция – непрерывная. Следовательно, существует повторный интеграл от этой функции по области :

или, окончательно,

(3)

Эта конструкция и называется повторным интегралом в . Ещё раз заметим, что вычисление такого интеграла производится справа налево! Избегайте грубых ошибок: в пределах интегрирования внутренних интегралов могут быть только внешние переменные.

Очевидно, что кроме рассмотренного порядка интегрирования (сначала по , потом по и, наконец, по ) существуют и другие порядки, причём все они приводят к одному и тому же числу .

Пример 9. Расставить пределы интегрирования в повторном интеграле от функции по области ограниченной поверхностями , , , .

Решение. Все указанные поверхности – это плоскости: и – координатные, – параллельна координатной . Вместе с четвёртой плоскостью они ограничивают некий тетраэдр. Его проекция на – это треугольник ограниченный осями , и прямой, которая является проекцией линии пересечения граней и . Исключая переменную из этих уравнений, получим уравнение проекции: .

Итак, для точек области имеем: 1) абсцисса изменяется от 0 до 2; 2) для каждого фиксированного ордината изменяется от 0 до прямой , т.е. до ; 3) аппликата изменяется от плоскости до плоскости , т.е. до . Стандартная запись области:

Повторный интеграл имеет вид:

.

Ещё раз напомним: вычисления производятся справа налево!