– 160–

Тема криволинейные интегралы

§1. Криволинейный интеграл 1го рода: определение, свойства, смысл

I Определение

Рассмотрим простую спрямляемую линию (плоскую или пространственную) и пусть на ней задана некоторая функция , . Выполним знакомую процедуру.

1^й_шаг. Разобьём линию произвольными точками … , на частей. Длину -ой части обозначим и пусть .

2^й_шаг. На каждой частичной дуге выберем произвольную точку

3^й_шаг. Составим интегральную сумму

Определение. Если при существует конечный предел интегральных сумм, не зависящий от разбиения линии на части и от выбора точек на этих частях, то этот предел называют криволинейным интегралом 1^го рода от функции по линии и обозначают символом

В системе координат используют обозначения

или

Линию называют путём интегрирования.

II Свойства

1) – длина пути интегрирования.

2) Линейность. 3) Аддитивность.

4) – криволинейный интеграл 1^го рода не зависит от направления обхода пути интегрирования.

III Смысл

А. Механический. Пусть вдоль линии распределена масса с линейной плотностью или . Тогда – это приближённое значение массы частичной дуги, а интегральная сумма приближённо равна массе всей линии. Точное же значение массы даёт криволинейный интеграл 1^го рода

В. Геометрический. Рассмотрим цилиндрическую поверхность , образующие которой параллельны оси , а направляющая – некоторая линия в плоскости . Как определить площадь части , заключённой между поверхностями и ? Линию разбиваем на частичные дуги Образующие, проходящие через точки деления, разобьют поверхность на отдельные полоски. Каждую такую полоску можно приближённо считать прямоугольником с основанием и высотой , где – некоторая точка из , Таким образом, интегральная сумма даёт приближённое значение искомой площади. Точное значение этой площади даётся интегралом

Грубо говоря, написанный интеграл – это площадь «забора» с основанием и переменной «высотой»

§2. Вычисление криволинейного интеграла 1го рода

I Явное задание пути интегрирования

Теорема. Пусть – часть графика непрерывно-диффе-ренцируемой функции а функция определена и непрерывна вдоль . Тогда:

1) криволинейный интеграл 1^го рода от функции вдоль существует;

2) этот интеграл можно вычислить по формуле

(1)

Доказательство. Из первой части теоремы, которую принимаем без доказательства, следует, что разбиение на части и выбор точек в этих частях (1^й и 2^й шаги процедуры) можно производить так, как нам удобно.

Разобьём промежуток точками на части. Тогда точки разбиения линии имеют вид . Для вычисления длины дуги используем соответствующую формулу и теорему о среднем:

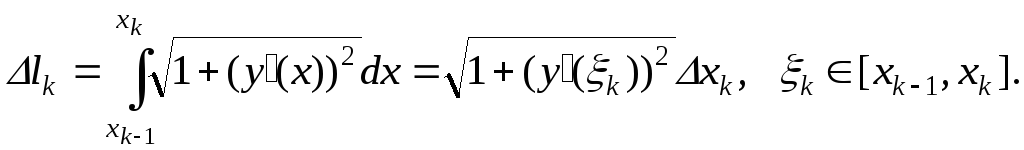
В качестве точки берём точку с координатами . Тогда интегральная сумма для криволинейного интеграла

есть не что иное, как интегральная сумма для определённого интеграла от функции на промежутке . Предел этой суммы и даст интеграл из (1).

Замечание 1. В случае, когда формула (1) принимает вид

Пример_1. Вычислить где –график функции , а .

Решение. Выполним предварительные вычисления:

Используем формулу (1)