II Определение

Пусть вдоль простой незамкнутой линии задана вектор-функцияПроведем привычную уже процедуру.

1^й_шаг. Линию произвольными точкамиразбиваем на частичные дугии обозначаемпроекции дугина осиисоответственно. Кроме того, пусть .

2^й_шаг. На каждой частичной дуге выбираем произвольную точку:

3^й_шаг. Составляем интегральную сумму

Определение. Если при существует конечный предел интегральных сумм, не зависящий от разбиения путина части и от выбора точекв этих частях, то такой предел называют криволинейным интегралом 2^го рода от вектор-функции по путии обозначают символом

(1)

Из первой части параграфа вытекает механический смысл интеграла (1) – это работа силового поля по перемещению единичной массы вдоль линии.

Замечание 2. Понятие интеграла (1) очевидным способом распространяется на случай трёхмерного силового поля

Замечание 3. Если путь интегрирования замкнут (но простой!), то по умолчанию считаем что он пробегается точкой против часовой стрелки (другими словами, область, которую ограничивает путь, остается при движении слева). В этом случае используют обозначение

Называют такой интеграл циркуляцией поля вдоль контура. Для пространственных замкнутых путей требуются дополнительные условия.

III Свойства

1. Линейность.

2. Аддитивность.

3. При изменении направления обхода пути интегрирования

криволинейный интеграл 2^го рода меняет знак на противоположный:

.

Это связано с тем, что проекции всех частичных дуг на оси, то есть всеизменят знак, а, следовательно, изменят знак и интегральная сумма и её предел.

4. Если – отрезок прямой, параллельный осиОх, то .

Если – отрезок прямой, параллельный осиОy, то .

Это следствие того, что, если, например, , то проекции всехна осьОy равны 0, поэтому интегральная сумма имеет вид Случайаналогичен.

Если у нас есть возможность выбора пути интегрирования, то можно выбрать ломанную, звенья которой, параллельны осям координат.

5. Формула Грина

где – область, которую ограничивает контур(L). Точная формулировка и доказательство будут даны ниже.

§5. Вычисление криволинейного интеграла 2го рода

I Явное задание пути интегрирования

Теорема 1. Пусть путь – это часть графика непрерывно-дифференцируемой функции, причем начало пути соответствует значению, а конец. Пусть, кроме того, вектор-функциянепрерывна вдоль. Тогда:

1) криволинейный интеграл 2^го рода от вектор-функции вдоль путисуществует; 2) этот интеграл можно вычислить по формуле

(1)

Доказательство. Докажем вторую часть теоремы, принимая во внимание первую часть (смотри доказательство теоремы 1, §2).

1^й_шаг. Разбиваем отрезок на части точкаминачастей. Тогда линияразобьётся на частичные дуги точками. Проекции дугина оси координат:по теореме Лагранжа.

2^й_шаг. В качестве точки возьмём точку с координатами .

3^й_шаг. Составляем интегральную сумму

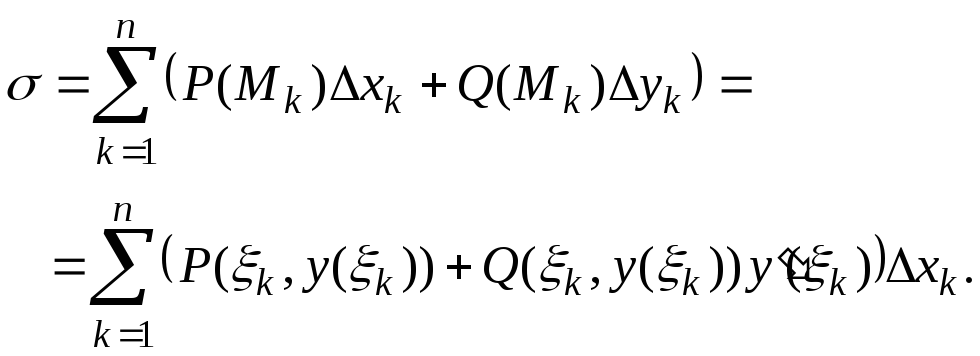
Последняя сумма – это интегральная сумма для определенного интеграла в формуле (1). Заметим, что условие равносильно условию

.

При доказательстве мы считали, что . Если же наоборот, то деление отрезкаи

Мы снова получили формулу (1).

Замечание 1. Если путь интегрирования , то формула аналогичная.

Пример 1. Вычислить криволинейный интеграл

,

где О(0,0), А(2,4) для случаев: а) (ОА) – дуга параболы ;b) (ОА) – двухзвенная ломанная .

Решение.

а) .

b) .

Здесь и. Поэтому .

Если рассмотреть интеграл от той же вектор-функции по замкнутому контуру , то нетрудно получить