§8. Нахождение функции по её полному дифференциалу

Теорема 1. Пусть функции непрерывны в ограниченной правильной области . Для того, чтобы выражение было полным дифференциалом некоторой функции необходимо и достаточно, чтобы в области выполнялось условие

(1)

При этом сама функция восстанавливается по полному дифференциалу с помощью криволинейного интеграла 2^го рода:

(2)

Доказательство. Необходимость. Если , то (по определению) и . Теорема о равенстве смешанных производных доказывает равенство (1).

Достаточность. Равенство (1) обеспечивает независимость от пути (теорема из §7). В доказательстве леммы 2, §7, мы уже построили функцию такую, что . Эта функция имеет вид (2); криволинейный интеграл можно свести к определённому, например, таким образом:

.

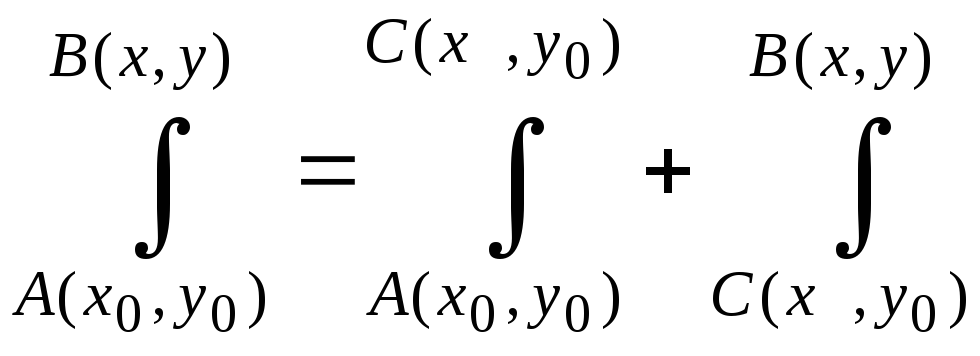Тогда получим выражение функции двух переменных через её частные производные первого порядка:

Замечание 1. Условие правильности области было введено лишь для упрощения доказательства формулы Грина. На самом же деле всё доказанное в этом и предыдущем параграфах имеет место для т.н. односвязной области:

плоская область называется односвязной, если каков бы не был замкнутый контур , ограниченная этим контуром часть плоскости целиком принадлежит (другими словами, область не содержит “дыр”).

Всё доказанное можно свести в такую теорему.

Теорема 2. Пусть функции непрерывны в ограниченной замкнутой односвязной области . Тогда следующие четыре утверждения равносильны:

1)

2) по любому контуру .

3) интеграл не зависит от пути в ;

4) выражение является полным дифференциалом некоторой функции.

Действительно, из 1) следует 2) в силу формулы Грина. Далее из 2) следует 3) (лемма 1), а из 3) следует 4) в силу леммы 2. И, наконец, из 4) следует 1) в силу теоремы о равенстве смешанных производных.

Замечание 2. Примем без доказательства, что выражение является полным дифферен-циалом некоторой функции , если выполняются равенства:

(3)

Как и в двумерном случае, эта функция восстанавливается криволинейным интегралом 2^го рода:

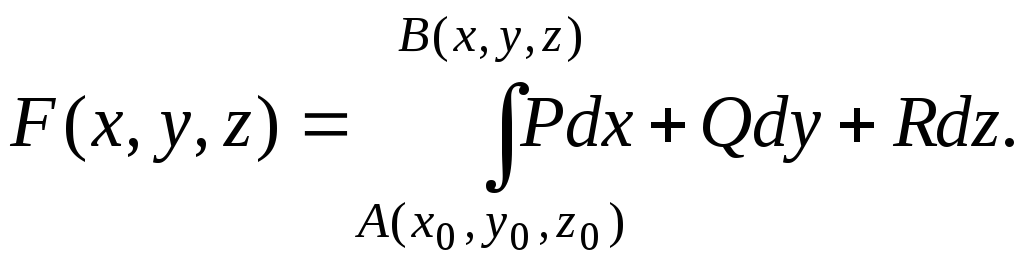
Если в качестве пути выбрать ломанную, звенья которой параллельны осям координат, то получим выражение через определённые интегралы:

Пример2. Убедиться, что выражение

является полным дифференциалом некоторой функции и найти эту функцию.

Решение. Выпишем и и найдём их производные:

Равенства (3) выполняются, значит, данное выражение – это полный дифференциал некоторой функции. Эта функция имеет вид (в качестве пути интегрирования выберем начало координат):