– 68–

Тема НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

В теме «Определенный интеграл» было рассмотрено понятие определенного интеграла для случая конечного промежуткаи ограниченной функции(см. теорему 1 из §3). Теперь займемся обобщением этого понятия для случаев бесконечного промежутка и неограниченной функции. Необходимость такого обобщения показывают, например, такие ситуации.

1. Если, используя формулу для длины дуги, попытаться вычислить длину четверти окружности ,, то придем к интегралу от неограниченной функции:

, где .

2. Пусть тело массой движется по инерции в среде с силой сопротивления , где— скорость тела. Используя второй закон Ньютона (, гдеускорение), получим уравнение:, где. Нетрудно показать, что решением этого (дифференциального!) уравнения является функция Если нам потребуется вычислить путь, пройденный телом до полной остановки, т.е. до момента, когда , то придем к интегралу по бесконечному промежутку:

§1. Несобственные интегралы 1-го рода

I Определение

Пусть функция определена и непрерывна на промежутке. Тогда для любогоона интегрируема на промежутке, то есть существует интеграл.

Определение 1. Конечный или бесконечный предел этого интеграла при называют несобственным интегралом 1-го рода от функциипо промежуткуи обозначают символом. При этом, если указанный предел конечен, то несобственный интеграл называют сходящимся, в противном случае (или не существует ) – расходящимся.

Итак, по определению

(1)

Примеры

1..

2..

3.– не существует.

Несобственный интеграл из примера 1 сходится, в примерах 2 и 3 интегралы расходятся.

II Формула Ньютона – Лейбница для несобственного интеграла первого рода

Пусть — некоторая первообразная для функции(сущест-вует на, т.к.— непрерывна). Тогда

Отсюда ясно, что сходимость несобственного интеграла (1) равносильна существованию конечного предела. Если этот предел обозначить, то можно написать для интеграла (1) формулу Ньютона-Лейбница:

, где .

Примеры.

4. .

5. .

6. Более сложный пример: . Сначала найдем первообразную:

Теперь можем найти интеграл _{, учитывая, что} :

.

III Свойства

Приведем ряд свойств несобственного интеграла (1), которые вытекают из общих свойств пределов и определенного интеграла:

1. интегралы и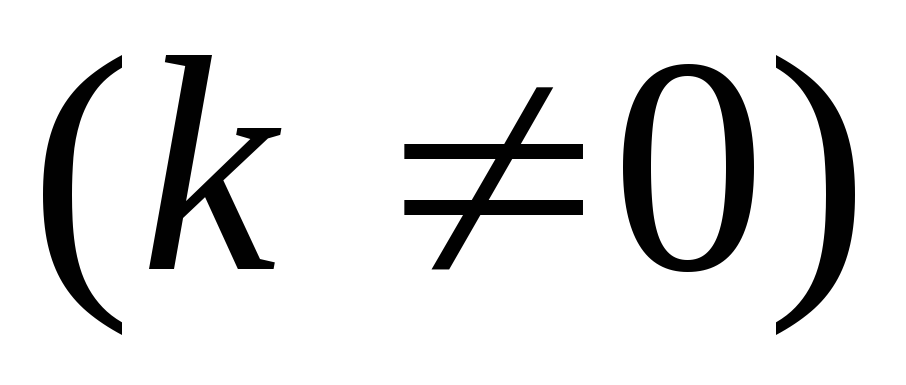сходятся или расходятся одновременно;

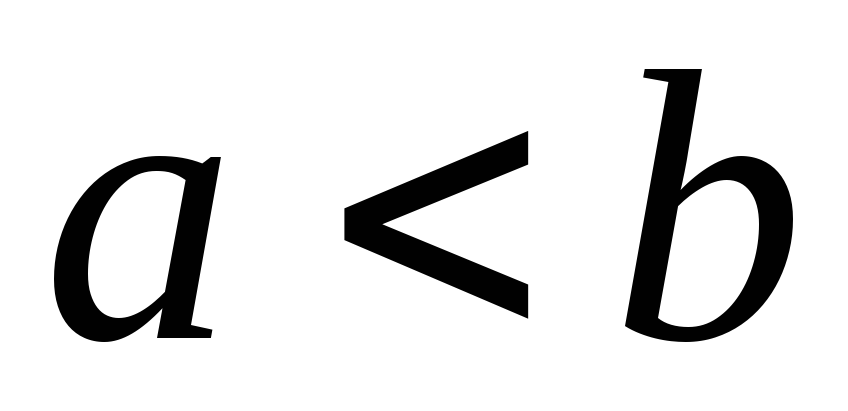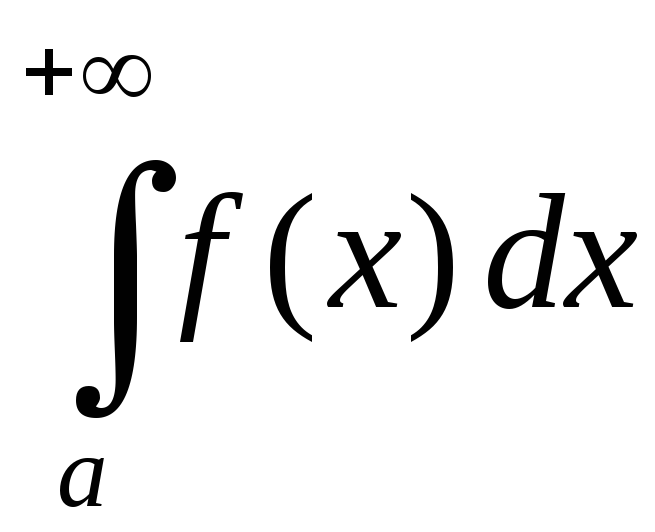2. если , то интегралыисходятся или рас-ходятся одновременно;

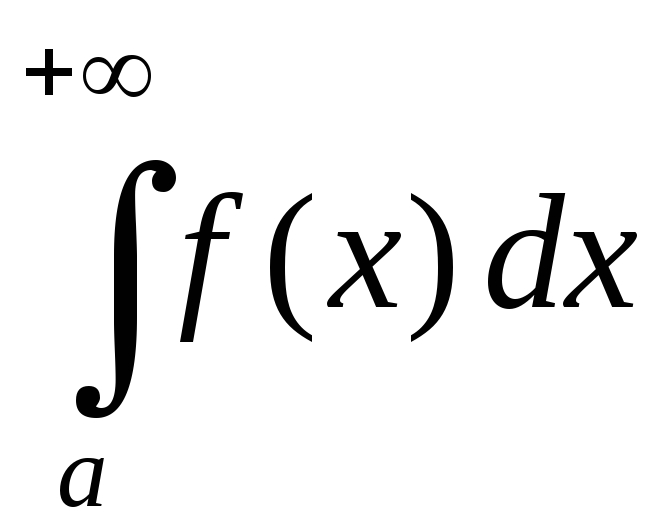3. если интеграл сходится, то.

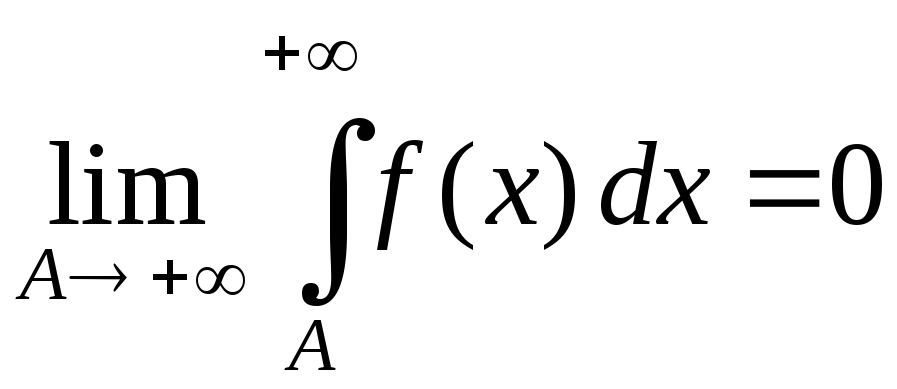IV Другие определения

Определение 2. Если непрерывна на , то

.

Определение 3. Если непрерывна на, то принимают по определению

(– произвольное),

причем несобственный интеграл в левой части сходится, если только оба ин-теграла в правой части сходятся.

Для этих интегралов, как и для интеграла (1) можно написать соответствующие формулы Ньютона – Лейбница.

Пример 7.

§2. Признаки сходимости несобственного интеграла 1-го рода

Чаще всего несобственный интеграл вычислить по определению не-возможно, поэтому используют приближенное равенство

(для больших ).

Однако, это соотношение имеет смысл лишь для сходящихся интегралов. Необходимо иметь методы выяснения поведения интеграла минуя определение.

I Интегралы от положительных функций

Пусть на ^. Тогда определенный интеграл как функция верхнего предела есть функция возрастаю-щая (это следует из общих свойств определенного интеграла).

Теорема 1. Несобственный интеграл 1^го рода от неотрицательной функ-ции сходится тогда и только тогда, когда функция остается ограниченной при увеличении.

Эта теорема – следствие общих свойств монотонных функций. Практического смысла теорема почти не имеет, но позволяет получить т.н. признаки сходимости.

Теорема 2 (1-й признак сравнения). Пусть функции инепре-рывны наи удовлетворяют неравенству. Тогда:

1) если интеграл сходится, то исходится;

2) если интеграл расходится, то ирасходится.

Доказательство. Обозначим: и. Так как, то. Пусть интегралсходится, тогда (в силу теоремы 1) функция‒ ограничена. Но тогда иограничена, а значит, интегралтоже сходится. Аналогично доказывается и вторая часть теоремы.

Этот признак не применим в случае расходимости интеграла от или сходимости интеграла от. Этот недостаток отсутствует у 2-го признака сравнения.

Теорема 3 (2-й признак сравнения). Пусть функции инепрерывны и неотрицательны на. Тогда, еслипри, то несобственные интегралыисходятся или расходятся одновременно.

Доказательство. Из условия теоремы получим такую цепочку равно-сильных утверждений:

, ,

.

Пусть, например, . Тогда:

.

Применим теорему 2 и свойство 1) из §1 и получим утверждение теоремы 3.

В качестве эталонной функции, с которой сравнивают данную, высту-пает степенная функция ,. Предлагаем студентам самим доказать, что интеграл

сходится при и расходится при.

Примеры. 1. .

Рассмотрим подынтегральную функцию на промежутке :

, .

Интеграл сходится, ибо. По 2-му признаку сравнения сходится и интеграл, а в силу свойства 2) из §1 сходится и исход-ный интеграл.

2..

Так как , тоcуществует такое, что при. Для таких значений переменной:

.

Известно, что логарифмическая функция растет медленнее степенной, т.е.

,

а значит, начиная с некоторого значения переменной, эта дробь меньше 1. Поэтому

.

Интеграл сходится как эталонный. В силу 1-го признака сравнения сходится и. Применяя 2-й признак, получим, что и интегралсходится. И снова свойство 2) из §1 доказывает сходимость исходного интеграла.