II Двойной интеграл в полярной системе координат

Известные формулы ,осуществляют взаимно-однозначное отображение полуполосыв системе на всю плоскость . Исключение составляет отрезок , которому соответствует единственная точка . Якобиан этой системы функций имеет вид

J.

Итак, для перехода в двойном интеграле от декартовой системы координат к полярной имеем формулу

Замечание 1. Переход в ПСК рекомендуется в случае, когда область интегрирования есть круг или его часть.

Пример 2. Вычислить двойной интеграл , где

Решение.

Замечание 2. В случае, когда область интегрирования есть эллипс

(или его часть), рекомендуется переход в обобщенную

полярную систему координат

якобиан которой .

Задачи.

1.Переходя в подходящую систему координат, вычислить площадь криволинейного четырёхугольника, ограниченного линиями ,,

2. Вычислить объём тела, ограниченного поверхностями ,(параболоид вращения).

§5. Приложения двойного интеграла

І Вычисление площади плоской фигуры

Пример 1. Вычислить площадь фигуры, ограниченной замкнутой линией

Решение. От данного – декартового – уравнения линии перейдём к полярному:

После упрощения получим

В силу симметрии линии относительно обеих осей (переменные и входят в уравнение в чётных степенях), достаточно рассматривать часть области, лежащую в первой четверти. Выражение для имеет смысл при

В первой четверти это условие выполняется при . Итак, рассматриваемая часть фигуры лежит между лучами и и для каждого полярные радиусы не превосходят . Находим площадь:

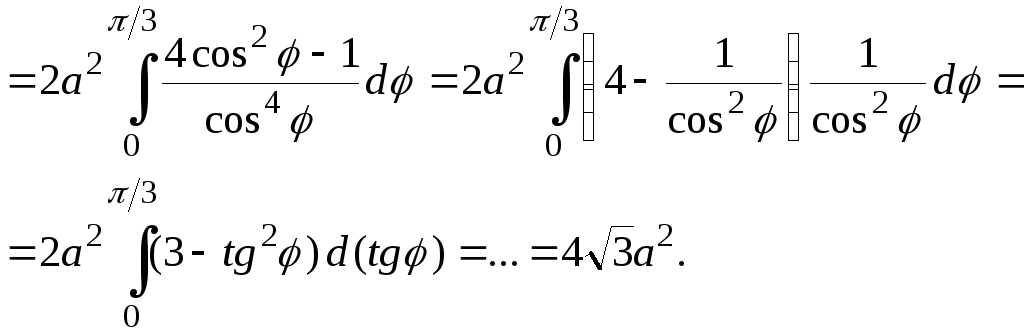
ІІ Вычисление объёмов тел

А. Объём цилиндри- ческого тела

Отметим, что кроме этой формулы можно написать ещё две аналогичные. Речь идёт о случаях, когда “основание” тела лежит в плоскости или , а “крыша” задаётся, соответственно, неотрицательной функцией или

Пример 2. Вычислить объём тела, ограниченного поверхностями

y

x

z

1

2

x

1

y

2

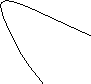
Решение. Поверхность – это цилиндрическая поверхность, образующие которой параллельны оси ординат (переменной нет в уравне-

нии!), а направляющей служит парабола в плоскости . Поверхности и – координатные плоскости и соответственно, а – плоскость, параллельная оси . Проекция тела на плоскость , т.е. его “основание” – это прямоугольник . Однако, над одной его частью “крышей” служит плоскость , а над другой частью “крыша” – это параболический цилиндр . Поэтому, при сведении двойного интеграла к повторному необходимо разбить на две части.

Лучше спроектировать тело на плоскость . В этой плоскости “основание” данного тела – это параболический сегмент . “Крышей” в этом случае служит плоскость , т.е. .

Итак, имеем для объёма

B. Тело ограничено двумя поверхностями и, причёми его проекция на плоскость – это плоская область :

И ещё две аналогичные формулы для случая проектирования на другие координатные плоскости.

Пример3. Найти объём тела, ограниченного поверхностями (верхняя часть конуса) и (“опрокинутый” и сдвинутый вверх параболоид).

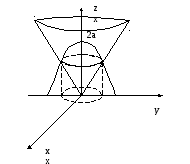
Решение. Если из системы уравнений конуса и параболоида исключить переменную , то получим уравнение границы проекции тела на плоскость :

или Решив это квадратное (относи-тельно ) уравнение получим =R (второй корень посторонний). Итак, – это круг радиуса с центром в , и поэтому лучше перейти в ПСК: