§2. Понятие повторного интеграла

I Правильные области в r2

Определение 1. Область плоскости называют правильной в направлении оси , если она ограничена линиями , , , , причём для функции и непрерывны и удовлетворяют неравенству .

Такую область можно записать следующим (стандартным) образом:

.

Геометрически правильность в направлении означает следующее: всякая прямая, проходящая через внутреннюю точку области параллельно оси , пересекает границу области ровно в двух точках.

Аналогичным образом определяется правильность области в направлении оси : .

Область называют правильной, если она правильна в направлении обеих осей.

Пример 1. Область ограничена линиями (парабола), (прямая) и (ось ). Записать область в стандартном виде.

Решение. Точки области имеют ординаты из отрезка .Зафиксируем из этого отрезка и проведём (слева направо) прямую параллельную оси . Она войдёт в область на прямой, где , а выйдет на правой ветви параболы, где . Значит, точки области с ординатой имеют абсциссы из промежутка . Запись области:

Эту же область можно записать и в другом виде, используя её правильность в направлении оси . Но запись будет сложнее, ибо верхняя граница области состоит из двух частей: прямой и параболы. Имеем:

Приведём еще два характерных примера правильных областей (во втором студенты очень часто делают ошибку в записи области).

Пример 2. Область ограничена линиями .

Пример 3. Область задана неравенством

Замечание 1. Неправильную область часто удаётся разбить на правильные части прямыми, параллельными осям координат.

Замечание 2. В полярной системе координат правильная область определяется аналогично: , где и – непрерывные функции. Геометрически: любой луч, выходящий из полюса и проходящий через внутреннюю точку области, пересекает её границу в двух точках.

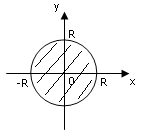
Пример 4. Круг радиуса с центром в полюсе записать в стандартной форме.

Решение. Для точек такого круга полярный угол изменяется в пределах от 0 до , а полярный радиус (для любого !) изменяется от 0 до . Запись области:

Пример 5. Область, ограниченную окружностью , записать в стандартной форме в ПСК.

Решение. Если уравнение окружности переписать в виде , то легко получить полярное уравнение этой окружности: . И из рисунка, и из самого уравнения видно, что область лежит между лучами и . Если зафиксировать полярный угол, , то точки круга лежат на хорде, вдоль которой полярный радиус изменяется от 0 (полюс) до (окружность). Итак, запись области

Заметим, что область, неправильная в ДПСК, может быть правильной в ПСК. Примером служит кольцо, у которого центр находится в начале координат:

II Правильные области в r3

Определение 2. Область из (с ДПСК) называют правильной в направлении оси , если она ограничена поверхностями , и цилиндрической поверхностью, образующие которой параллельны оси , а направляющая ограничивает правильную область на плоскости .

Геометрически такая правильность означает следующее: проекция на плоскость – это правильная плоская область , а прямая, проходящая через внутреннюю точку параллельно оси , пересекает границу области в двух точках.

Такую область можно записать в виде

или, если учесть правильность в направлении оси ,

Аналогично определяется правильность области в направлении других осей. Если область является правильной в направлении всех координатных осей, её называют просто правильной. Заметим, что для правильной области существует 3! способов записи в стандартной форме.

Пример 6. Область ограничена поверхностями (цилиндрическая), (коническая) и (параболоид вращения). Записать в одной из стандартных форм.

Решение. Проекцией тела на плоскость является круг . Тогда .

Через точку , лежащую в этом круге, проведём (снизу вверх) прямую, параллельную оси . Эта прямая войдёт в область на конусе, а выйдет на параболоиде. Таким образом, окончательно будем иметь:

Заметим, что, решая задачу, мы считали область расположенной внутри цилиндра. Но те же поверхности ограничивают еще одну область – вне цилиндра. Проекцией этой области на плоскость является кольцо с внутренним радиусом . Внешний радиус найдём, если из системы

определяющей линию пересечения конуса и параболоида, исключим .Получим т.е. внешний радиус кольца . Однако, кольцо в ДПСК – это неправильная область. Её можно разбить на две правильные части с составными границами или на четыре части с простыми границами. Для таких случаев ниже будут предложены другие системы координат в (цилиндрическая и сферическая).