
- •Тема кратные интегралы
- •§1. Определения. Свойства. Смысл
- •I Определение
- •II Теорема существования
- •III Свойства
- •IV Смысл
- •§2. Понятие повторного интеграла
- •I Правильные области в r2
- •II Правильные области в r3
- •III Повторные интегралы в r2
- •IV Повторные интегралы в r3
- •§3. Вычисление кратных интегралов
- •§4. Замена переменных в двойном интеграле
- •I Общий случай
- •II Двойной интеграл в полярной системе координат
- •§5. Приложения двойного интеграла
- •III Вычисление массы полоской фигуры
- •IV Вычисление координат центра масс пластины
- •V Вычисление моментов инерции пластины
- •VI Вычисление площади поверхности
- •§6. Замена переменных в тройном интеграле
- •I Общий случай
- •II Тройной интеграл в цилиндрических координатах
- •III Тройной интеграл в сферических координатах
- •§7. Приложения тройного интеграла
- •I Вычисление объёмов тел
- •II Вычисление масс тел
- •III Вычисление координат центра масс тела
- •IV Вычисление моментов инерции тела
- •V Вычисление силы притяжения точки телом
- •§8. Несобственный двойной интеграл
§6. Замена переменных в тройном интеграле
I Общий случай
Пусть имеем две
прямоугольные системы координат в
пространстве
![]() и
и![]() ,
и систему функций
,
и систему функций
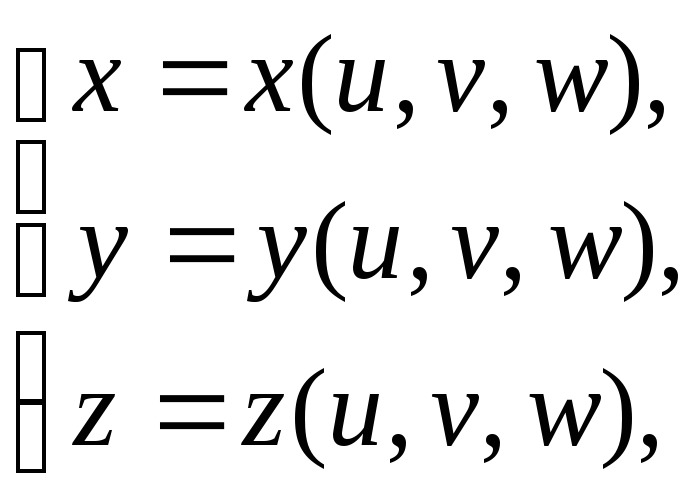 (1)
(1)
которые устанавливают
взаимно-однозначное соответствие между
точками некоторых областей
![]() и
и![]() в этих системах координат. Предположим,
что функции системы (1) имеют в
в этих системах координат. Предположим,
что функции системы (1) имеют в![]() непрерывные частные производные.
Определитель, составленный из этих
частных производных
непрерывные частные производные.
Определитель, составленный из этих
частных производных
 ,
,
называют якобианом
(или определителем Якоби) системы функций
(1). Мы будем предполагать, что
![]() в
в![]() .
.
В сделанных выше предположениях имеет место следующая общая формула замены переменных в тройном интеграле:

Как и в случае
двойного интеграла, взаимная однозначность
системы (1) и условие
![]() могут нарушаться в отдельных точках,
на отдельных линиях и на отдельных
поверхностях.
могут нарушаться в отдельных точках,
на отдельных линиях и на отдельных
поверхностях.
Система функций
(1) каждой точке
![]() ставит в соответствие единственную
точку
ставит в соответствие единственную
точку![]() .
Эти три числа
.
Эти три числа![]() называют криволинейными координатами
точки
называют криволинейными координатами
точки![]() .
Точки пространства
.
Точки пространства![]() ,
для которых одна из этих координат
сохраняет постоянное значение, образуют
т.н. координатную поверхность.
,
для которых одна из этих координат
сохраняет постоянное значение, образуют
т.н. координатную поверхность.
II Тройной интеграл в цилиндрических координатах
Цилиндрическая
система координат (ЦСК) определяется
плоскостью
![]() ,
в которой задана полярная система
координат и осью
,
в которой задана полярная система
координат и осью![]() ,
перпендикулярной этой плоскости.
Цилиндрическими координатами точки
,
перпендикулярной этой плоскости.
Цилиндрическими координатами точки![]() пространства называют тройку чисел
пространства называют тройку чисел![]() ,
где
,
где![]() – полярные координаты точки
– полярные координаты точки![]() – проекции т
– проекции т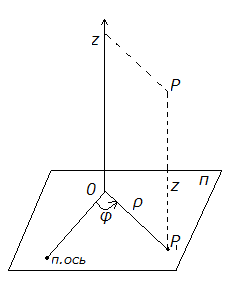 очки
очки![]() на плоскость
на плоскость![]() ,
а
,
а![]() – это координаты проекции точки
– это координаты проекции точки![]() на ось
на ось![]() или
или![]() .
.
В плоскости
![]() введем обычным образом декартовы
координаты, ось аппликат направим по
оси
введем обычным образом декартовы
координаты, ось аппликат направим по
оси![]() ЦСК. Теперь нетрудно получить формулы,
связывающие цилиндрические координаты
с декартовыми:
ЦСК. Теперь нетрудно получить формулы,
связывающие цилиндрические координаты
с декартовыми:
 (3)
(3)
Эти формулы
отображают область![]()
![]() на все пространство
на все пространство![]() .
.
Координатными поверхностями в рассматриваемом случае будут:
1)
![]() – цилиндрические поверхности с
образующими, парал-лельными оси
– цилиндрические поверхности с
образующими, парал-лельными оси
![]() ,
направляющими которых служат окружности
в плоскости
,
направляющими которых служат окружности
в плоскости![]() ,
с центром в точке
,
с центром в точке![]() ;
;
2)
![]() – полуплоскости, проходящие через ось
– полуплоскости, проходящие через ось
![]() ;
;
3)
![]() – плоскости, параллельные плоскости
– плоскости, параллельные плоскости
![]() .
.![]()
Якобиан системы (3):
 .
.
Общая формула в случае ЦСК принимает вид:
![]()
Замечание 1.
Переход к
цилиндрическим координатам рекомендуется
в случае, когда область интегрирования
– это круговые цилиндр или конус, или
параболоид вращения (или их части),
причем ось этого тела совпадает с осью
аппликат
![]() .
.
Замечание 2. Цилиндрические координаты можно обобщить так же, как и полярные координаты на плоскости.
Пример 1. Вычислить тройной интеграл от функции
![]()
по области
![]() ,
представляющей собой внутреннюю часть
цилиндра
,
представляющей собой внутреннюю часть
цилиндра![]() ,
ограниченную конусом
,
ограниченную конусом![]() и параболоидом
и параболоидом![]() .
.
Решение. Эту область мы уже рассматривали в §2, пример 6, и получили стандартную запись в ДПСК. Однако, вычисление интеграла в этой области затруднительно. Перейдем в ЦСК:
 .
.
Проекция
![]() тела
тела![]() на плоскость
на плоскость![]() – это круг
– это круг![]() .
Следовательно, координата
.
Следовательно, координата![]() изменяется от 0 до
изменяется от 0 до![]() ,
а
,
а![]() – от0
до R.
Через
произвольную точку
– от0
до R.
Через
произвольную точку
![]() проведем прямую, параллельную оси
проведем прямую, параллельную оси![]() .
Прямая войдет в
.
Прямая войдет в![]() на конусе, а выйдет на параболоиде. Но
конус
на конусе, а выйдет на параболоиде. Но
конус![]() имеет в ЦСК уравнение
имеет в ЦСК уравнение![]() ,
а параболоид
,
а параболоид![]() – уравнение
– уравнение![]() .
Итак, имеем
.
Итак, имеем
 .
.
III Тройной интеграл в сферических координатах
Сферическая система
координат (ССК) определяется плоскостью
![]() ,
в которой задана ПСК, и осью
,
в которой задана ПСК, и осью![]() ,
перпендикулярной плоскости
,
перпендикулярной плоскости![]() .
.
Сферическими
координатами точки
![]() пространства называют тройку чисел
пространства называют тройку чисел![]() ,
где
,
где![]() – полярный угол проекции точки на
плоскость
– полярный угол проекции точки на
плоскость![]() ,
,![]() – угол между осью
– угол между осью![]() и вектором
и вектором![]() и
и![]() .
.
В плоскости
![]() введем декартовы координатные оси
введем декартовы координатные оси![]() и
и![]() обычным образом, а ось аппликат совместим
с осью
обычным образом, а ось аппликат совместим
с осью![]() .
Формулы, связывающие сферические
координаты с декартовыми таковы:
.
Формулы, связывающие сферические
координаты с декартовыми таковы:
 (4)
(4)
Эти формулы
отображают область
![]() на всё пространство
на всё пространство![]() .
.
Якобиан системы функций (4):
 .
.
Координатные поверхности составляют три семейства:
1)
![]() – концентрические сферы с центром в
начале координат;
– концентрические сферы с центром в
начале координат;
2)
![]() – полуплоскости, проходящие через ось
– полуплоскости, проходящие через ось
![]() ;
;
3)
![]() – круговые конусы с вершиной в начале
координат, осью которых служит ось
– круговые конусы с вершиной в начале
координат, осью которых служит ось
![]() .
.
Формула перехода в ССК в тройном интеграле:

Замечание 3.
Переход в ССК рекомендуется, когда
область интегрирования – это шар или
его часть. При этом уравнение сферы
![]() переходит в
переходит в![]() .
Как и ЦСК, рассмотренная ранее, ССК
«привязана» к оси
.
Как и ЦСК, рассмотренная ранее, ССК
«привязана» к оси![]() .
Если центр сферы смещён на радиус вдоль
координатной оси, то наиболее простое
сферическое уравнение получим при
смещении вдоль оси
.
Если центр сферы смещён на радиус вдоль
координатной оси, то наиболее простое
сферическое уравнение получим при
смещении вдоль оси![]() :
:
![]() .
.
Замечание 4. Возможно обобщение ССК:

с якобианом
![]() .
Эта система функций переведет эллипсоид
.
Эта система функций переведет эллипсоид
![]()
в «параллелепипед»
![]() .
.
Пример
2. Найти
среднее расстояние точек шара радиуса
![]() от его центра.
от его центра.
Решение.
Напомним, что среднее значение функции
![]() в области
в области![]() – это тройной интеграл от функции по
области деленный на объём области. В
нашем случае
– это тройной интеграл от функции по
области деленный на объём области. В
нашем случае
![]() .
.
Итак, имеем

