Діюче значення першої гармоніки фазної і лінійної напруги:

, .

Фазна напруга (рис.4.63) має три рівні: перший рівень з амплітудою 2/3U при відносній тривалості α₁=5/6, другий рівень з амплітудою 2/3U при відносній тривалості α₂=3/6 і третій рівень з амплітудою 4/3U при відносній тривалості α₃=1/6. Діюче значення фазної напруги

.

Коефіцієнти викривлення і гармонік фазної напруги: ν=0.986, К_ГН=THD=16.67.

Напруга ключа схеми .

При чотирьох рівнях напруги згідно табл. 4.17 на рис.4.64 побудовані діаграми напруги у фазах навантаження, чому відповідає третій рівень просторового вектору. При цьому період вихідної напруги розподілено на 18 інтервалів часу (18 базових ненульових вектори), фазна напруга на навантаженні має 13 рівнів, лінійна 7.

Таким чином, тривалість знаходження вектора в кожному з положень (тривалість кожної сходинки напруги навантаження на рис.4.63 і рис.4.64) Δt=T/6h (Т –період вихідної напруги). При вихідній частоті f₂ цьому відповідає еквівалентна частота модуляції f_M=6hf₂. Кількість рівнів и_Н (включаючи 0) складає N=3h+1. Частота f₂ може бути будь-якою і регулюватися плавно.

Реалізація припускає розбиття Т на 6h інтервалів, при побудові використані принципи, що розглянуто у п.4.3.1. Слід відзначити, що формування напруги має певні закономірності, про що мова йде нижче.

Слід зазначити, що наявність надлишкових станів дозволяє одне і теж и_Нодержати при різних алгоритмах перемикання напруги у фазах БАІН. Відповідні діаграми дляh=1 подані на рис.4.65. Мінімальна кількість перемикань відповідаєи_БАІН1, проте при несиметрії напруги щодо нуля різним буде навантаження джерел постійного струму. Тому доцільним буде використання варіантуи_БАІН2 з симетрією напруги фази БАІН відносно нуля. Для парних значеньh напруга фази БАІН симетрична відносно нуля. Кількість рівнів відмінних від нуля в напівхвилі напруги БАІНi= h/2.

На рис.4.66 приведені діаграми напруги фази БАІН і навантаження для h=1, 2,…, 6.

П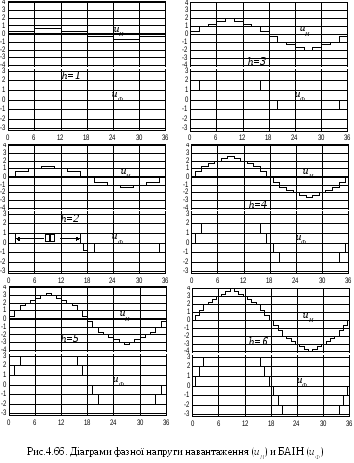ри відомій напрузі у фазах БАІН напруги у фазах навантаження можуть бути розраховані, використовуючи метод вузлової напруги для еквівалентної схеми трифазного БАІН (рис.4.67).

Напруга U_nN

де Y_А=Y_В=Y_С- провідність гілок навантаження.

При симетричному навантаженні провідності фаз однакові і рівні Y. Далі нескладно визначити напруги на фазах навантаження (U_а, U_в, U_с)

и_Ф=е_Ф - и_nN . (4.52)

При h=1 (рис.4.62, рис.4.65) напрузі фази БАІНи_БАІН2відповідає стандартне розкладання в ряд Фур'є [20]:

, (4.53)

де U - напруга джерела постійного струму (перший рівень), значення відносної тривалості позитивної і негативної напівхвиліα=1/3.

Вузлова напруга

. (4.54)

Відповідно до (4.54) вузлова напруга приймає нульове значення для всіх гармонік окрім кратних трьом (оскільки напруги в фазах БАІН мають зсув на 2π/3 і утворюють симетричну трифазну систему). З урахуванням (4.52) фазна напруга на навантаженні визначається виразом (4.53) за винятком гармонік кратних 3. Амплітуда 1-ї гармоніки

.

Таким чином, амплітуда першої гармоніки фазної напруги навантаження U_m(1)=2U/π, амплітуди вищих гармонік:

(4.55)

де n=1,2,3..

Це можна віднести і для всіх рівнів напруги, тобто гармонійний склад и_Н однозначно визначається напругою фази БАІН, що спрощує його аналіз.

При h=2 (рис.4.66) напруга фази БАІНи_БАІН симетрична щодо нуля, тривалість позитивної і негативної його півхвиль складаєαπ=5π/6, де .

Напруга фази БАІН визначається згідно (4.53).

Відповідно до визначеного вище, у фазній напрузі навантаження маємо ті ж гармонійні складові (за винятком гармонік кратних трьом). Амплітуда 1-ї гармоніки

.

Кратність вищих гармонік k=6n±1.

При парних значеннях h відносна тривалість, що відповідає даному рівню напруги (значення i=1, 2, 3..) визначається як

. (4.56)

Амплітуда гармонік напруги з кратністю ν

, (4.57)

де k=6n±1 іn=1, 2, 3….

При непарних значеннях h амплітуда гармонік напруги

. (4.58)

Так при h=5 вираз (4.58) має вигляд

.

Період вихідної напруги на фазі навантаження можна розділити на 6h інтервалів . Кількість рівнів в напівхвилі вихідної напруги на фазі навантаженняр=2h, причому один рівень становить ( у відносних одиницях 1/3). Принцип формування напруги на фазі навантаженняu_Н при парних і непарних h має свої закономірності. Це стосується здвоєних на інтервалі рівнів, кількість яких k₂. При парних значеннях h напівхвиля напруги u_Н починається зі здвоєних рівнів. При непарних значеннях h здвоєні рівні відраховуються, починаючи з другого рівня.

Для визначення діючого значення досить врахувати тільки чверть періоду. При цьому тривалість останнього ступеня становить половину інтервалу, кількість цілих інтервалів, де напруга відмінна від нуля – j.

При непарних h=1,3,5,… ,.

Відносне значення напруги на i - інтервалі (ступені):

, якщо i≤k₂.

, якщо i>k₂.

Діюче значення напруги

.

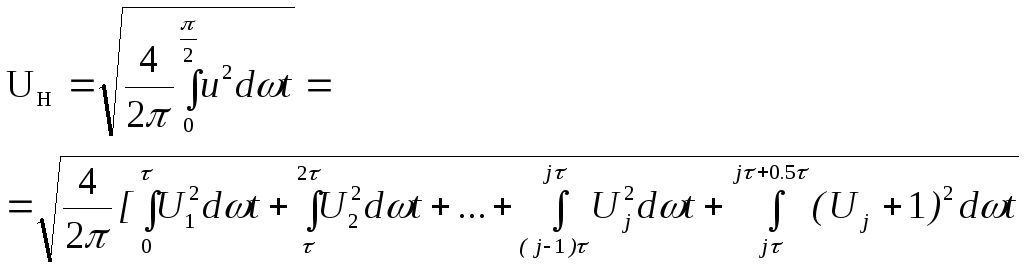Після перетворення отримуємо

. (4.59)

При парних h=2,4,6,… ,.Відносне значення напруги на i - інтервалі (ступені): , якщоi≤k₂. , якщоi>k₂.

Діюче значення напруги визначається відповідно з (4.59).

Коефіцієнт гармонік (THD) .

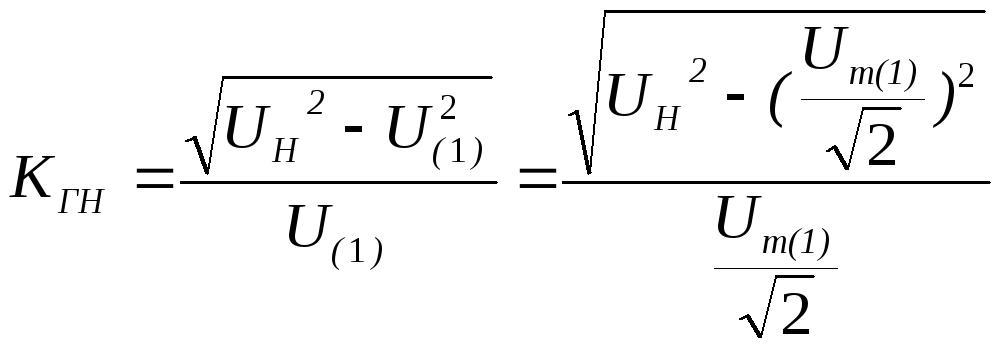Результати розрахунку гармонійного складу напруги навантаження приведені в табл.4.6. Максимальне значення амплітуди першої гармоніки подане в табл.4.5. Слід відзначити, що інтегральний показник THD достатньо низький, проте великі значення гармонік низького порядку. Спектр напруги (відносні значення напруги по відношенню до 1-ї гармоніки) при h=3 приведений на рис.4.68. Аналіз спектру напруги на навантаженні БАІН показує, що максимальна амплітуда гармонік має місце при кратності ν=6n·h±1. Якнайгірший випадок має місце при h=1, коли амплітуда гармонік визначається виразом (4.55) і 5- а гармоніка складає 20% від основної.

Таблиця 4.5

Максимальне значення амплітуди першої гармоніки

h	1	2	3	4	5	6	8
Um(1)	0.637U	1.23U	1.833U	2.437U	3.045U	3.653U	4.867U

Таблиця 4.6

Гармонійний склад напруги

h	2	3	4	5	6	7	8	9	10	11	12	13
THD,%	16.7	11.55	9.06	7.60	6.69	6.06	5.63	5.30	5.06	4.86	4.72	4.59
U5, %	5.29	4.49	4.23	4.14	4.05	4.02	4.01	4.00	3.99	3.98	3.98	3.98
U7, %	3.90	12.59	2.39	8.24	2.21	6.44	2.15	5.46	2.12	4.83	2.11	4.41
U11, %	9.11	7.97	1.21	4.84	0.97	3.65	0.91	3.00	0.88	2.60	0.87	2.32
U13, %	7.68	1.79	1.00	0.83	0.73	0.67	0.66	0.65	0.63	0.63	0.62	0.62

Квантування за рівнем. У схемі БАІН як і у інших типів інверторів можливо амплітудне регулювання вихідної напруги. Воно можливо як за рахунок змінювання кількості рівнів вихідної напруги, так і за рахунок змінювання тривалості кожного рівня при незмінній загальній кількості рівнів (звичайно у певних межах).

Ціль багаторівневого формування напруги – отримати її максимально наближеною до синусоїди. При цьому згідно заданій синусоїді необхідно визначити тривалість роботи окремих АІН. Найбільш просто це здійснити при дискретизації синусоїди за рівнем – квантуванні, що можливо двома методами.

Перший – квантування з похибкою (рис.4.69), коли перехід на наступний рівень здійснюється по досягненні заданою напругою u_ЗАД=Asinωt (A – відносне значення амплітуди першої гармоніки фазної напруги до напруги одного рівня джерела U) визначеного рівня (U, 2U, 3U,…) з шагом ∆=U (U - напруга окремого джерела). У результаті отримуємо напругу східчастої форми u_СХ та напругу похибки квантування u_П=(u_ЗАД - u_СХ).

Можливо використання іншого методу квантування з усередненням, коли середнє значення похибки на інтервалі Δt, що відповідає тривалості окремої сходинки дорівнює нулю. При цьому використовується більш точний принцип квантування за рівнем з умови порівнювання на інтервалі квантування площі синусоїди та апроксимуючого її прямокутника (рис.4.72). Реалізація такого варіанта достатньо складна. При спрощенні – заміні на інтервалі квантування ділянки синусоїди на пряму лінію, цей метод (рис.4.70) може бути достатньо просто реалізований зсувом рівнів квантування відносно вісі абсцис наΔ=U/2. Тобто рівні квантування становлять 0.5U; 1.5U; 2.5U;....

Слід відзначити, що у трифазній схемі за відсутністю нульового проводу форма напруги і її гармонійний склад безпосередньо на фазі навантаження покращується. Надалі при визначені напруги використовуються відносні одиниці за умови U=1.

Квантування за рівнем з усередненням(за середнім рівнем - рис.4.71). Діюче значення гармонік напруги з кратністю k

або

, (4.60)

де θ_i - кут, відповідний переходу на i - й рівень, i=1,2,…n – номер рівня (n≤A).

Виходимо з того, що гармонійний склад напруг фази МПЧ і фази навантаження відрізняється тільки наявністю гармонік кратних 3.

Діюче значення напруги фази

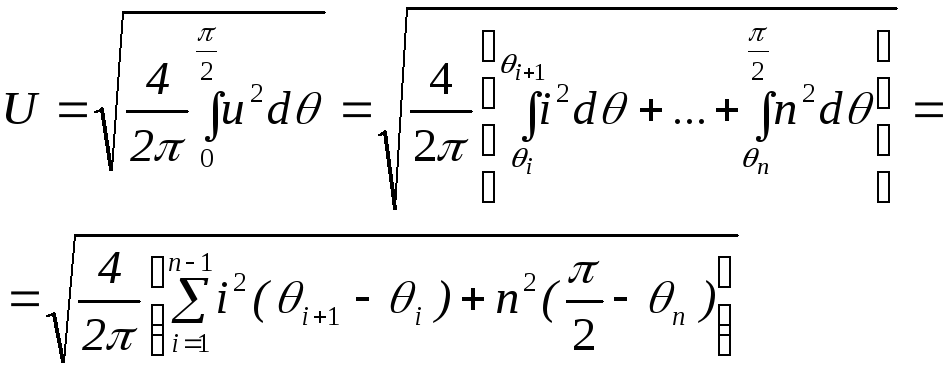
або .

Діюче значення напруги на фазі навантаження

,

де U₍₃₎ - U₍₁₅₎ – гармоніки кратні трьом (відповідно до (4.60)).

Коефіцієнт гармонік (THD) .

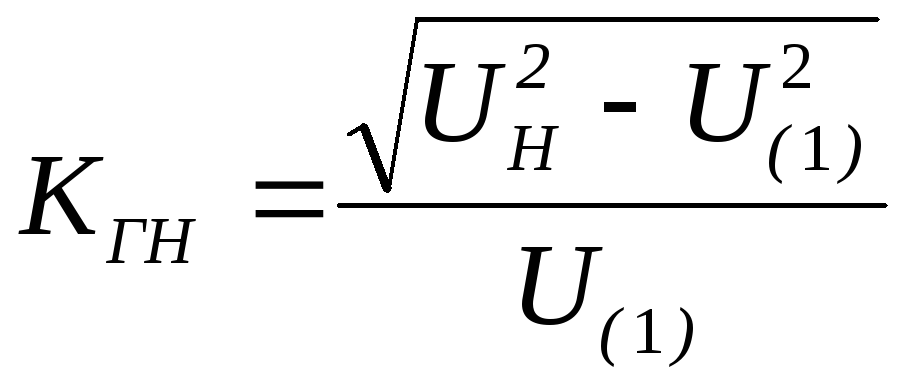Відносна похибка квантування по першій гармоніці:

.

Залежність К_ГН (А) з урахуванням 103 гармонік і відносні значення амплітуд 5-ї і 7-ї гармонік (стосовно першої) наведені в табл.4.7.

Таблиця 4.7

Гармонійний склад напруги

А	1	1.5	2	2.5	3	3.5	4	4.5	5	5.5	6	7
THD,%	30.6	17.8	15.6	10.8	9.6	8.1	7.2	6.7	6.5	5.8	5.1	3.7
U5, %	20	2.72	1.87	5.2	0.13	4	0.44	3	0.46	2.37	0.43	0.38
U7, %	14.3	11	6.5	0.37	2.0	1.62	0.62	1.82	0.13	1.7	0.06	0.13
Δ, %	10.3	20	3.75	9.4	2.06	5.7	1.35	3.9	0.97	2.9	0.74	0.59

Продовження таблиці 4.7

А	8	9	10	11	12	13	14
THD, %	3.8	3.4	2.6	2.5	2.3	2.15	2.0
U5, %	0.33	0.29	0.26	0.23	0.21	0.19	0.17
U7, %	0.16	0.17	0.17	0.16	0.15	0.14	0.14
Δ, %	0.48	0.4	0.34	0.3	0.26	0.23	0.2

Усереднення за площею.

Перемикання на черговий i-й рівень (i=1,2,…n) здійснюється з умови рівності площ ділянки синусоїди відповідного даному рівню і прямокутника, обмеженого кутом γ_i (рис.4.72). Площа ділянки синусоїди відповідного останнього рівня

.

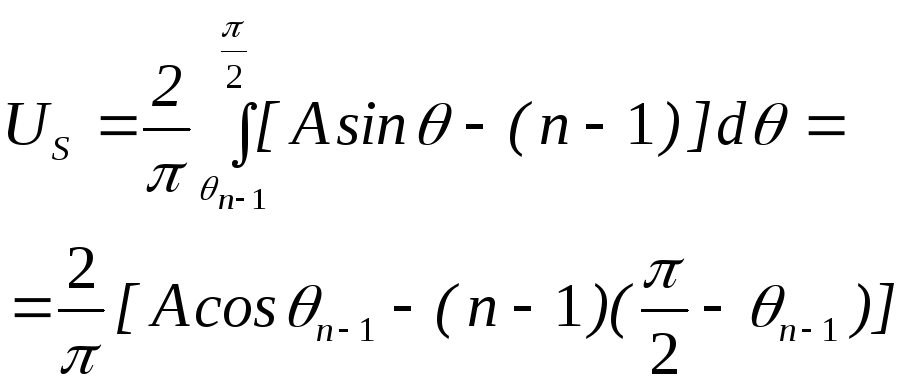Площа прямокутника, початок якого відповідає γ_n

.

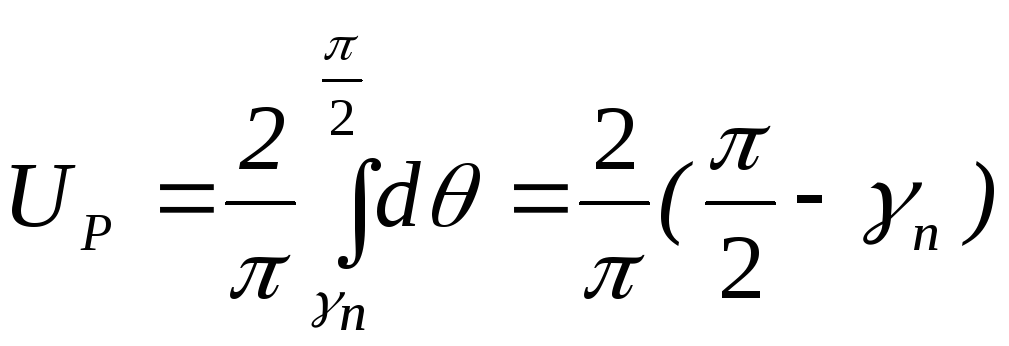На основі рівності площ .

Для інших рівнів площа ділянки синусоїди відповідає поточному рівню (i)

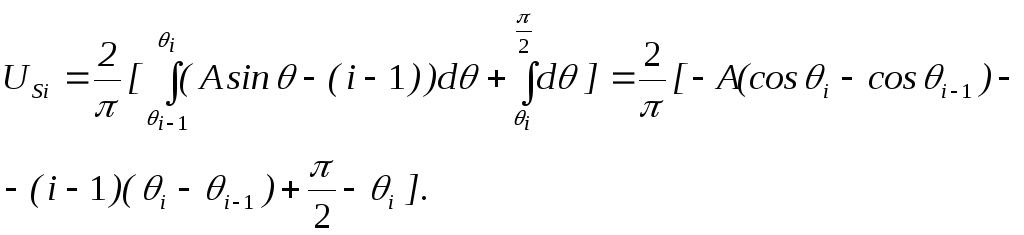
Звідси значення кута

Відносна амплітуда гармонік вихідної напруги

.

Коефіцієнт гармонік: .

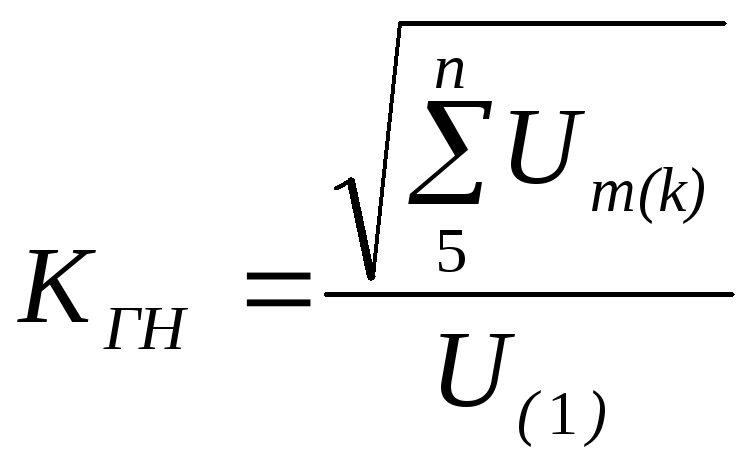У табл.4.8 наведено залежності для коефіцієнта гармонік і відносних значень гармонік низького порядку (по відношенню до першої) з урахуванням 103 гармонік.

Таблиця 4.8