65

4.3.2.2 Вибіркове формування з заданим гармонійним складом

Подавление высших гармоник низкого порядка (5-я, 7-я, 11-я, 13-я) при минимальном количестве переключений ключей достигается при избирательном (selective PWM) управлении [7, 9]. Даний принцип, зазвичай, пропонується для каскадних схем з послідовним з’єднанням інверторів. Його також можна використати для формування напруги у окремій фазі БАІН з декількома рівнями напруги джерела постійного струму.

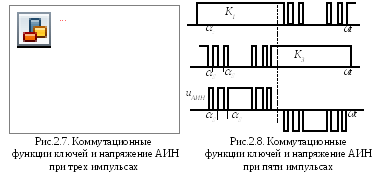
В этом плане интересны алгоритмы с избирательным формированием напряжения из трех (рис.2.7) или пяти (рис.2.7) импульсов, положение которых характеризуется углами α_i. На рис.2.7, рис.2.8 также показаны коммутационные функции ключей двух плеч АИН К₁ и К₃ при использовании однополярной модуляции для однофазного мостового АИН.

При этом амплитуда k-й гармоники напряжения (k=6l±1)

.

При трех импульсах моменты переключения (α_i) определяются из условия, что значения U₍₅₎=U₍₇₎=0 (k=5, k=7), при пяти импульсах U₍₅₎=U₍₇₎=U₍₁₁₎=U₍₁₃₎=0.

Расчеты [66] подтверждают возможность эффективного подавления 5-й и 7-й гармоник практически во всем диапазоне регулирования первой гармоники, для 11-й и 13-й только в узком диапазоне регулирования (0.9-1).

На рис.2.9 приведены значения углов α₁, α₂, α₃ при регулировании первой гармоники и поддержании 5-й и 7-й гармоник (u₅=U_m(5)/U_m(1), u₇=U_m(7)/U_m(1)) в диапазоне значений ±0.5%. Вариант зависимостей по результатам выборки значений α₁, α₂, α₃ приведен на рис.2.10.

В [180] приведены зависимости для α_i при пяти импульсах.

При последовательном соединении нескольких АИН дополнительные возможности подавления гармоник более высокого порядка (11-й и выше) обеспечивает метод, когда для подавления гармоник формирование напряжений АИН осуществляется со сдвигом на угол γ по основной гармонике [84, 66].

Принцип формирования применительно КМПЧ с двумя АИН на фазу иллюстрирует рис.2.11. При этом напряжение і - того из n АИН:

.

Результирующее (суммарное) значение амплитуды k- й гармоники:

.

Результирующая амплитуда k-ой гармоники при отсутствии сдвига по основной гармонике: .

Коэффициент ослабления k-й гармоники:

.

После преобразования получаем:

.

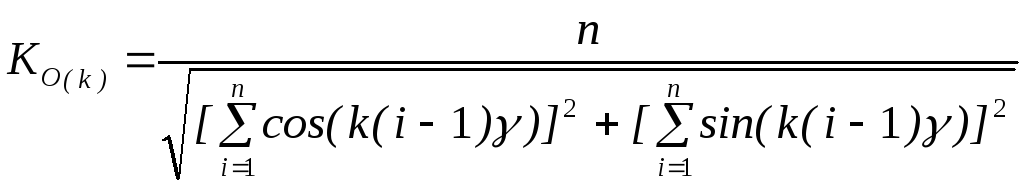Зависимость коэффициента ослабления К_0(k) от угла γ приведена на рис.2.12, рис.2.13 при n=2 и n=3 для k=11,13,17,19. Нетрудно заметить, что при определенных γ значение К_0(k)→∞ и достигается полное подавление k-ой гармоники. Значение соответствующего угла: (i =1, 2, 3,…).

Очевидно, что следует выбирать промежуточное значение γ из условия одновременного максимального подавления 11-й 13-й гармоник. Анализ показывает, что такое условие достигается при (на рис.2.12γ=15º, на рис.2.13 γ=10º). Соответствующие значения К_0(k) при этом приведены в табл.2.11.

Таблица 2.11

Коэффициент ослабления гармоник

n	2	3	4	5	6
КО(1)	1.009	1.010	1.011	1.011	1.011
КО(5)	1.260	1.313	1.331	1.34	1.344
КО(7)	1.643	1.781	1.832	1.855	1.868
КО(11)	7.661	9.495	10.19	10.52	10.704
КО(13)	7.661	10.51	11.62	12.158	12.456
КО(17)	1.6437	3.094	3.714	4.023	4.196
КО(19)	1.261	3.094	3.921	4.341	4.58

Наличие сдвига по основной гармонике обуславливает некоторое снижение основной гармоники – значения К_О(1) приведены в табл.2.11. Однако это снижение не существенно. При этом следует учитывать, что предельное значение первой гармоники напряжения отдельного АИН при α₁=α₂=α₃=π/12 соответствует второму уровню пространственного вектора напряжения и составляет в относительных единицах (при единичной амплитуде U_m=1) , что превышает предельное значение при векторной ШИМ (U*_m(1)=1.15).

Принцип подавления можно объяснить исходя из следующих соображений: 11-я и 13-я гармоники являются боковыми для 12-й гармоники. В периоде выходной частоты укладывается двенадцать периодов гармоники, соответственно, ее период составит 2π/12. Полное подавление гармоники достигается приn=2, если гармоники напряжений АИН, которые суммируются, будут в противофазе, что соответствуетγ=π/12. Дляn=3 сдвигγ=π/18соответствует сдвигу 12-й гармоникинапряжений АИН на треть периода, когда они образуют симметричную трехфазную систему и их сумма равна 0. Осциллограммы напряжений фазы МПЧ u_ФМПЧ и фазы нагрузки u_ФН при избирательном управлении со сдвигом γ=15º при n=2 приведены на рис.2.11.

При этом можно комбинировать использование трех (при μ>0.9) и пяти импульсов (при μ<0.9). Важным достоинством данного метода применительно КМПЧ является выравнивание загрузки АИН.

Некоторые особенности имеет реализация применительно МАИН с несколькими уровнями напряжения. Рассмотрим применение для пятиуровневого АИН (ПАИН). Обозначим логической переменной М₁ состояние ключей соответствующих первому уровню напряжения фазы МПЧ - при положительной полярности М_1Р при отрицательной М_1N, аналогично М_2Р и М_2N – для второго уровня. Закон изменения напряжения при заданных α_i соответствует логической переменной U_1P и U_1N. Аналогичное напряжение со сдвигом на угол γ соответствует переменной U_2P и U_2N. Связь между переменными определяется выражениями:

, ,,.