Примеры для самостоятельного решения

Найти общие решения уравнений:

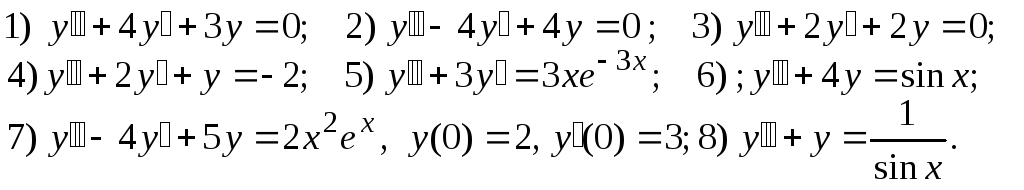
1.10. Системы дифференциальных уравнений

Литература: [1], гл. I, § 1.21

[3], гл. XIII, § 29

[5], Ч. 2, гл. 11, § 11.9

Нормальной системой дифференциальных уравнений называется совокупность n дифференциальных уравнений первого порядка вида

где x ─ независимая переменная, ─ искомые функции,─ производные первого порядка искомых функций. Здесь все уравнения разрешены относительно производных.

Решением нормальной системы из n дифференциальных уравнений называется совокупность таких n функций , при подстановке которых в уравнения системы последние обращаются в верные равенства.

Общим решением системы из n уравнений называется такое ее решение , которое содержитn произвольных постоянных , и из которого путем подбора этих постоянных можно получить частное решение системы, удовлетворяющее заданным начальным условиям (т.е. решение задачи Коши). Начальные условия для системы дифференциальных уравнений имеют вид, т.е. заданы значения функций в точке.

Одним из методов решения нормальных систем является метод исключения, который основывается на положении, что любую нормальную систему из n уравнений можно привести к дифференциальному уравнению n-го порядка.

Рассмотрим метод исключения на примере.

Пример 1. Решить систему дифференциальных уравнений

.

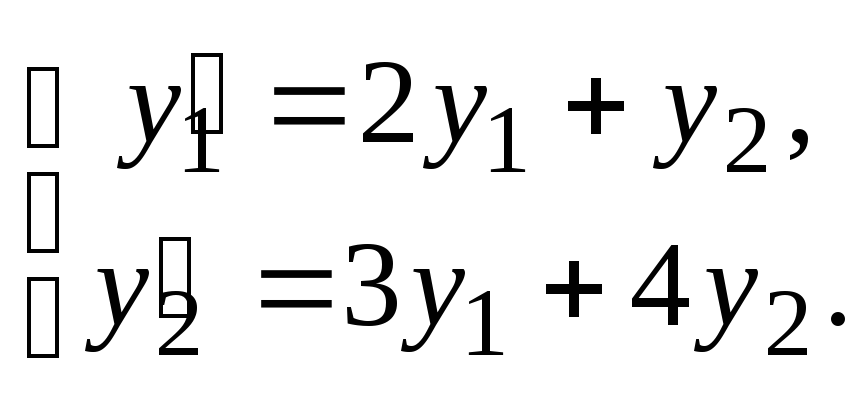Решение. Из первого уравнения выразим функцию через функциюи ее производную. Откуда. Подставляем значенияиво второе уравнение системы. Получаем уравнение. Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнениеимеет действительные корнии. Поэтому. Теперь определяем вторую функцию.

Ответ: ,.

Пример 2. Найти решение системы дифференциальных уравнений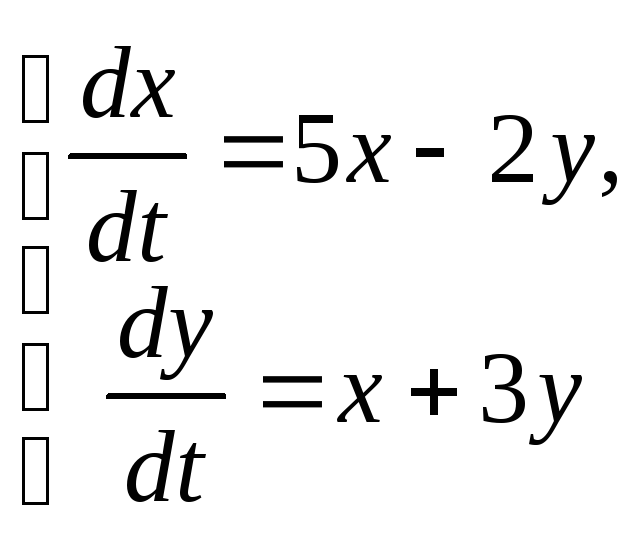удовлетворяющее условию.

Решение. Обратим внимание, что искомые функции иявляются функциями независимой переменнойt.

Обозначим ,. Тогда система примет вид

Из второго уравнения системы . Тогда. Подставив значенияив первое уравнение системы, получим. Это линейное однородное уравнение с постоянными коэффициентами, характеристическое уравнение которогоимеет пару комплексных корней. Значит,и. Тогда.

Решаем задачу Коши. . ОтсюдаЗначит, решение системы, удовлетворяющее заданным начальным условиям, имеет вид.

Примеры для самостоятельного решения

Решить систему дифференциальных уравнений:

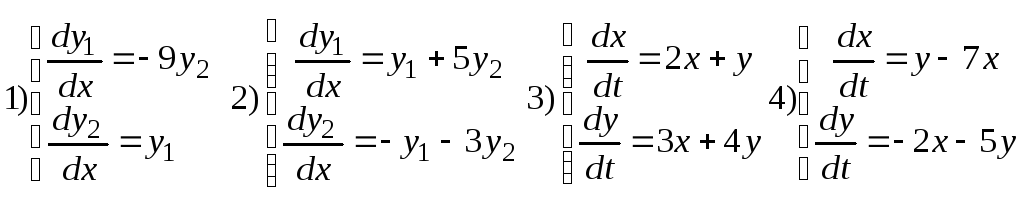
2. Числовые ряды

2.1 Основные понятия

Литература: [1], гл. I, § 1.2

[3], гл. XIII, § 2

[5], Ч. 3, гл. 15, § 15.1

Рядом называется выражение вида , где, называемые членами ряда, являются членами бесконечной последовательности. Они могут быть числами, функциями, матрицами и соответствующие ряды называются числовыми, функциональными, матричными.

Сокращенно ряд обозначается символом , гденазываетсяобщим членом ряда.

Сумма n первых членов ряда называетсячастичной суммой.

Если при неограниченном увеличении числа слагаемых числового ряда существует конечный предел частичной суммы , то он называетсясуммой ряда и записывается . Числовой ряд в этом случае называетсясходящимся. В противном случае (предел частичной суммы не существует или равен бесконечности) ряд называется расходящимся. Расходящийся ряд суммы не имеет.

Из определения сходящегося и расходящегося рядов непосредственно вытекают следующие теоремы:

1) отбрасывание от ряда или присоединение к нему любого конечного числа начальных членов не меняет его сходимости или расходимости;

2) умножение всех членов ряда на любое отличное от нуля действительное число не влияет на сходимость ряда.

Для сходящихся рядов справедливы следующие теоремы:

1) если сходящийся ряд , имеет суммуS, то ряд , гдеλ − любое действительное число, имеет сумму λS.

2) если сходящиеся ряды иимеют суммыS_a и S_b соответственно, то ряд также сходится, а его сумма равнаS_a + S_b.