Примеры для самостоятельного решения

Найти область сходимости следующих рядов:

1); 2); 3);

4) ; 5); 6) .

3.3. Дифференцирование и интегрирование степенных рядов

Степенной ряд можно почленно дифференцировать и интегрировать на любом отрезке, целиком принадлежащем интервалу сходимости. Полученный при этом ряд имеет тот же интервал сходимости и его сумма внутри этого интервала равна соответственно производной и интегралу от суммы первоначального ряда.

Пример 1. Найти сумму ряда .

Решение. Вначале найдем промежуток, где данный ряд сходится.

.

Следовательно, интервал сходимости ряда (-1, 1). Исследуем ряд на его границах. При ряд имеет вид(гармонический ряд, расходится). Приполучаем сходящийся (по признаку Лейбница) знакочередующийся ряд. Итак, область сходимости данного ряда ─ промежуток [-1, 1).

Возьмем теперь ряд вида . Приего сумма легко считается:.

Почленное интегрирование этого ряда дает заданный ряд: . Поэтому.

3.4. Ряды Тейлора и Маклорена. Разложение функций в степенные ряды

Литература: [5], Ч. 3, гл. 15, § 15.8

Рядом Тейлора для бесконечно дифференцируемой в точке и некоторой ее окрестности функцииназывается степенной ряд вида

Необходимое и достаточное условие сходимости этого ряда к функции , т.е. условие того, что , есть . Здесь R_n(x) – остаточный член ряда Тейлора. Одно из его выражений, полученное Лагранжем, имеет вид , где с – некоторая точка, определяемая выражением .

Заметим, что при получаем ряд вида

,

который называется рядом Маклорена.

Для разложения функции в степенной ряд используют следующие приемы.

І. Функция непосредственно разлагается в ряд Тейлора, что производят за несколько этапов:

а) вычисляют производные всех порядков функции в точкеи формальноcоставляют ряд Тейлора;

б) находят область сходимости полученного ряда;

в) выполняют проверку условия , т. е. определяют сходимость ряда к функции .

2. Используют табличные разложения:

;

;

;

;

;

.

3. Используют сложение (вычитание) рядов и умножение ряда на некоторое выражение.

Например, если,то ряд дляумножают на.

4. Используют дифференцирование и интегрирование рядов.

Например, для функции ряд можно получить дифференцированием ряда.

5. Используют умножение рядов, производимое по правилу умножения многочленов. Так можно, например, получить ряд для функции .

Пример. Разложить в ряд по степеням функцию.

Решение. Полагая и используя табличное разложение функции, имеем

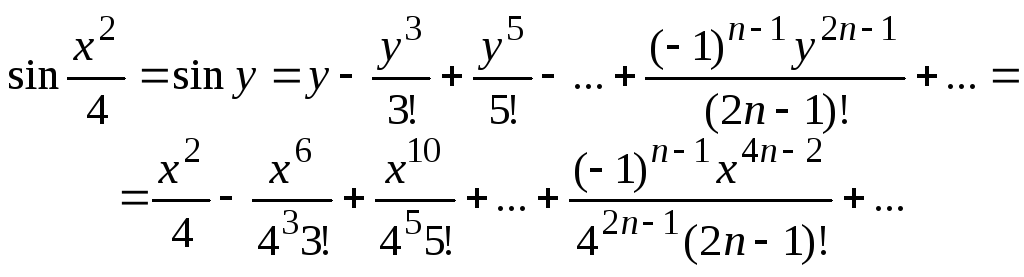
Для функции разложение получаем, умножая этот ряд на:

.

Это разложение справедливо при любом , так как разложение в ряд функцииимеет место при любом значении.

Примеры для самостоятельного решения

Разложить в ряд Маклорена следующие функции:

1) ; 2); 3).

3.5. Приложения степенных рядов

Литература: [5], Ч. 3, гл. 15, § 15.9

Для приближенного вычисления значения функции в некоторой точке можно использовать следующий прием. Разложить эту функцию в степенной ряд. В полученном разложении положить и в качестве приближенного значениявзять сумму определенного числа членов ряда (в зависимости от требуемой точности). Оценку точности находят на основании оценки остатка ряда, которая может быть произведена, например, следующим образом:

1) если ряд знакочередующийся, то ошибка не превышает по абсолютной величине модуля первого из отброшенных членов;

2) остаток ряда оценивается сравнением его с рядом убывающей геометрической прогрессии, сумма которого ;

3) если полученный числовой ряд удовлетворяет условиям интегрального признака Коши, то .

Пример 1. Вычислить приближенно , ограничиваясь первыми двумя членами ряда Маклорена для функции, и оценить получившуюся при этом погрешность.

Решение. При любом справедливо разложение

При имеем.

Приближенно в соответствии с заданным условием

.

Так как ряд знакочередующийся, то ошибка не превосходит первого из отброшенных членов .

Пример 2. Вычислить с точностью до 0,01.

Решение. .

Здесь заданное выражение представлено в виде суммы вида , гдеобязательно меньше 1 (для того, чтобы можно было использовать биномиальный ряд в его области сходимости). Затем используем разложение функциив биноминальный ряд

При с учетом того, что ряд знакочередующийся, подбором убеждаемся, что нужную точность обеспечивает сумма трех членов, так как

Тогда .

Неопределенные и определенные интегралы, а также некоторые несобственные интегралы, вычисляются аналогично (подынтегральная функция раскладывается в степенной ряд).

Пример 3. Вычислить с точностью до 0,01.

Решение. Разложим подынтегральную функцию в ряд

Отсюда

.

Здесь для получения заданной точности можно ограничиться суммой первых двух членов (т.к. ряд знакочередующейся и уже третий член меньше 0,01).

На практике способы интегрирования дифференциальных уравнений с помощью рядов применяют, когда решение дифференциального уравнения в элементарных функциях невозможно. Один из таких способов ─ способ последовательных дифференцирований, применяется, когда требуется найти частное решение, удовлетворяющее заданным начальным условиям. Тогда для целого ряда дифференциальных уравнений искомое решение можно искать в виде ряда Тейлора

Значение производных в точке определяется из начальных условий и последовательного дифференцирования данного дифференциального уравнения. Недостаток данного метода заключается в том, что обычно не удается найти формулу общего члена ряда.

Пример 4. Найти в виде степенного ряда решение дифференциального уравнения , удовлетворяющее следующим начальным условиям.

Решение. Решение ищем способом последовательного дифференцирования. Для этого искомую функцию у представляем в виде ряда Тейлора

Значения (из начальных условий). Значениеполучается непосредственно из дифференциального уравнения, приимеем.

Продифференцировав заданное уравнение, получим

.

Аналогично получаем производные более высокого порядка:

, ,...,.

Отсюда при получаем,,,…

Подставив эти значения в ряд, получаем частное решение в виде