2.5. Знакочередующиеся ряды. Признак Лейбница

Литература: [5], Ч. 3, гл. 15, § 15.4

Ряд называется знакочередующимся, если два любых его соседних члена отличаются знаками.

Для определения сходимости знакочередующихся рядов пользуются признаком Лейбница: знакочередующийся ряд сходится, если его члены убывают по абсолютной величине и предел его общего члена равен нулю при n→∞.

Пример 1. Исследовать на абсолютную и условную сходимость ряд .

Решение. Данный знакочередующийся ряд расходится, так как не выполняется необходимое условие сходимости ряда: не равен нулю.

Пример 2. Исследовать на абсолютную и условную сходимость ряд .

Решение. Рассмотрим ряд . Применим для исследования его на сходимость признак Даламбера:

.

Ряд сходится. Следовательно, данный ряд абсолютно сходящийся.

Примеры для самостоятельного решения

Исследовать на абсолютную и условную сходимость ряды:

а) ; б); в); г).

3. Функциональные ряды

3.1. Основные понятия

Литература: [5], Ч. 3, гл. 15, § 15.6

Ряд, членами которого являются функции от некоторого аргумента, называется функциональным:

.

При фиксированном значении x из функционального ряда получаем числовой ряд. Множество значений x, при которых получаемые числовые ряды сходятся, называется областью сходимости функционального ряда. Так как значение суммы ряда зависит от значения переменной x, то сумма функционального ряда также является функцией от x.

3.2. Степенные ряды. Интервал сходимости

Литература: [5], Ч. 3, гл. 15, § 15.7

Степенным рядом называется функциональный ряд вида

.

Здесь − числа, называемые коэффициентами ряда.

Заменой данный ряд приводится к виду.

Основное свойство степенных рядов состоит в том, что если степенной ряд сходится при, то он сходится и притом абсолютно при всяком значенииx, удовлетворяющем условию (теорема Абеля).

Одним из следствий этой теоремы является факт существования для каждого степенного ряда интервала сходимости (-R, R) c центром в начале координат, внутри которого степенной ряд абсолютно сходится, а вне его расходится. На концах интервала в точках и, ряд может сходится или расходиться. Числоназываетсярадиусом интервала сходимости ряда.

Легко заметить, что для ряда центром интервала сходимости является не начало координат, а точках=х₀ и интервал сходимости имеет вид .

Для отыскания радиуса сходимости можно использовать один из следующих способов.

1. Применить непосредственно обобщенный признак Даламбера или обобщенный радикальный признак Коши, т.е. находить интервал сходимости, решая неравенства:

или .

Здесь − общий член данного ряда.

2. Если среди коэффициентов ряда быть может лишь конечное число равных нулю, то

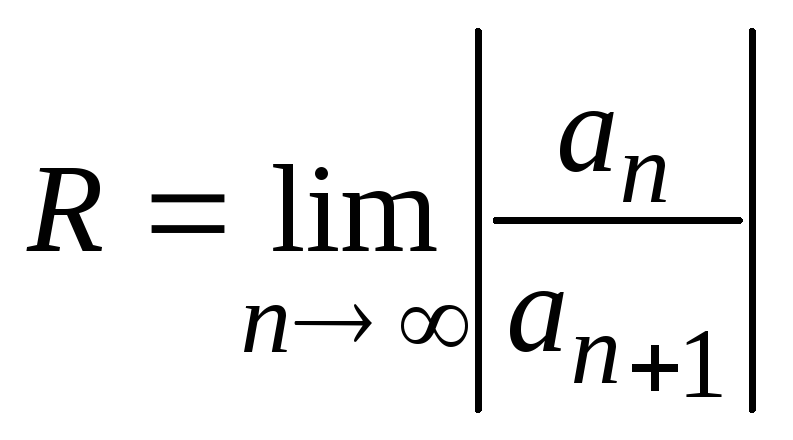или .

Пример 1. Найти область сходимости степенного ряда .

Решение. Для данного ряда , тогда.

Определяем радиус сходимости ряда:

.

Интервал сходимости ряда (-2, 2). Для определения области сходимости ряда, исследуем его в граничных точках интервала.

При ряд имеет вид, а при−. Эти ряды расходятся, так как предел общего члена каждого ряда приn→∞ отличен от нуля. Итак, область сходимости степенного ряда (-2, 2).

Пример 2. Найти область сходимости степенного ряда .

Решение. Здесь радиус интервала сходимости ряда удобнее вычислять по формуле

.

При ряд сходится, при остальных значенияхрасходится.

Пример 3. Найти область сходимости ряда.

Решение. Так как все коэффициенты при нечетных степенях х равны нулю, то вычислить радиус интервала сходимости непосредственно по формуле нельзя. Применим обобщенный признак Даламбера.

, .

Ряд сходится, если

Данное условие выполняется при любом значении х. Значит, ряд сходится на всей числовой оси ().