Примеры для самостоятельного решения

1. Вычислить с точностью до 0,001: а) ; б); в).

2. Вычислить с точностью до 0,001: а) ; б).

3. Найти в виде ряда решения следующих дифференциальных уравнений:

а) (до );

б) (до );

в) (до );

г) (до ).

4. Ряды Фурье. Разложение функций в ряд Фурье

Литература: [5], Ч. 3, гл. 15, §§ 15.10, 15.11

Ряд Фурье – это один из видов функционального ряда. Его членами являются тригонометрические функции, образующие ортогональную систему, а коэффициенты определяются по формулам Фурье. Тригонометрическая система функций

является ортогональной на промежутке [-l, l] (как впрочем на любом промежутке длиной 2l). Это означает, что интеграл по этому промежутку от произведения любых двух функций этой системы равен нулю.

Для функции, заданной на промежутке (-l, l), ряд Фурье имеет вид

,

его коэффициенты вычисляются по формулам Фурье

, ,.

Формально ряд Фурье можно составить для любой функции, интегрируемой на промежутке (-l, l). Условия, при которых сумма этого ряда равна заданной функции, определяются теоремой Дирихле: если периодическая функция f (x) имеет период 2l и является кусочно-гладкой в промежутке (-l, l), то ее ряд Фурье сходится при всех значениях х, причем в точках непрерывности функции сумма этого ряда равна значению функции, а в точках разрыва эта сумма равна среднему арифметическому предельных значений функции слева и справа в этих точках .

Заметим, что в ряд Фурье можно разложить и непериодическую кусочно-гладкую функцию f (x), заданную лишь в интервале (-l, l). Полученный ряд является сходящимся на всей числовой оси, а его сумма есть периодическое продолжение функции f (x) на всю числовую ось. Исключение составляют лишь точки разрыва, в которых сумма ряда равна среднему арифметическому левого и правого пределов периодического продолжения данной функции.

Если выполняются условия Дирихле, то функция разложима в ряд Фурье и в случае, когда она задана на отрезке [0, 2l] и даже на любом отрезке [а, а+2l].

В частных случаях, если функция f (x) – четная, то ее ряд Фурье содержит только косинусы:

.

Если функция f(x) – нечетная, то ее разложение содержит только синусы:

.

Замечание. Функция, заданная в интервале (0, l) может быть продолжена на промежуток (-l, 0) либо четным, либо нечетным образом и разложена в ряд Фурье по косинусам или по синусам.

Пример 1. Разложить в ряд Фурье заданную в промежутке функцию

Решение. Вычислим коэффициенты Фурье:

;

;

.

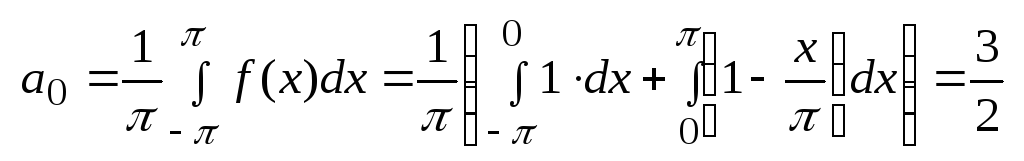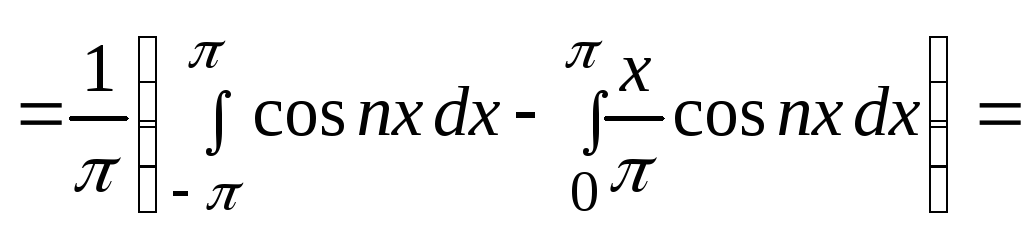
Искомое разложение имеет вид

.

График заданной функции изображен на рис. 1 (а), график суммы ряда Фурье ─ на рис. 1 (б).

_{Рис. 1}

Пример 2. Разложить функцию в ряд Фурье в интервале (0, 1) в ряд синусов.

Решение. Интервал (0, 1) не симметричен относительно начала координат. Продолжим функцию , заданную в интервале (0, 1), на интервал (-1, 0] нечетным образом (рис. 2).

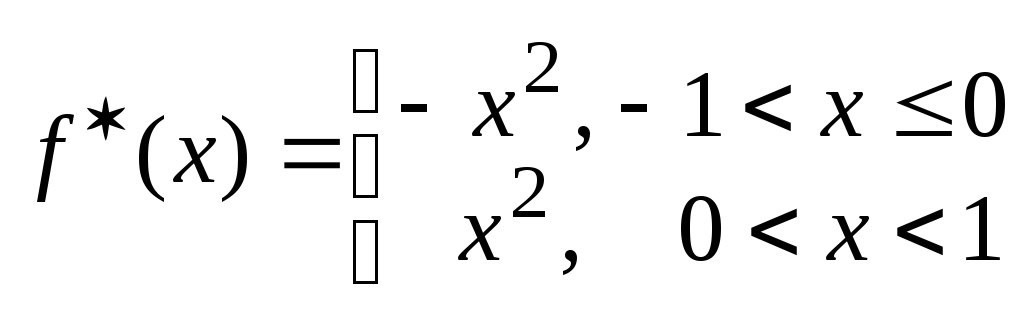Функциязадана на промежутке (-1, 1) и является нечетной. Значит, ее разложение в ряд Фурье содержит только синусы.

Вычисляем коэффициенты Фурье

.

Искомое разложение имеет вид

.

Задания для контрольных работ Контрольная работа № 5 «Дифференциальные уравнения»

Задание 1. Найти решение дифференциального уравнения первого порядка.

1.1.	а) ;	б) .
1.2.	а) ;	б) .
1.3.	а) ;	б) .
1.4.	а) ;	б) .
1.5.	а) ;	б) .
1.6.	а) ;	б) .
1.7.	а) ;	б) .
1.8.	а) ;	б) .
1.9.	а) ;	б) .
1.10.	а) ;	б) .

Задание 2. Найти решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами.

1.1.	а) ;	б) .
1.2.	а) ;	б) .
1.3.	а);	б) .
1.4.	а) ;	б).
1.5.	а) ;	б) .
1.6.	а) ;	б) .
1.7.	а) ;	б) .
1.8.	а) ;	б) .
1.9.	а) ;	б) .
1.10.	а) ;	б) .

Задание 3. Решить систему дифференциальных уравнений.

3.1.

3.2.

3.3.

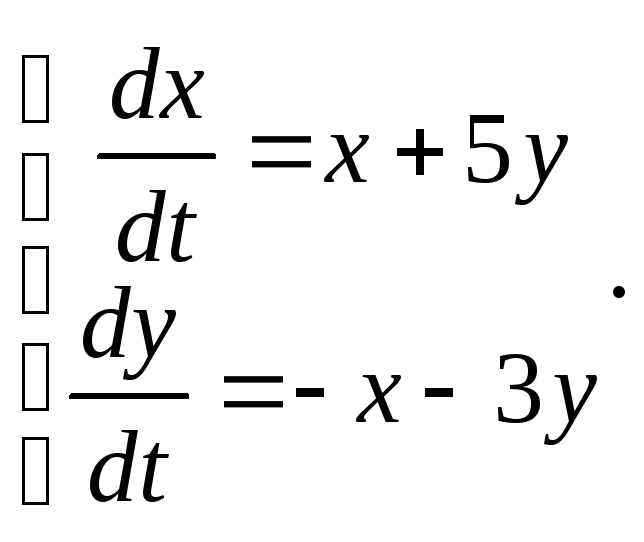
3.4.

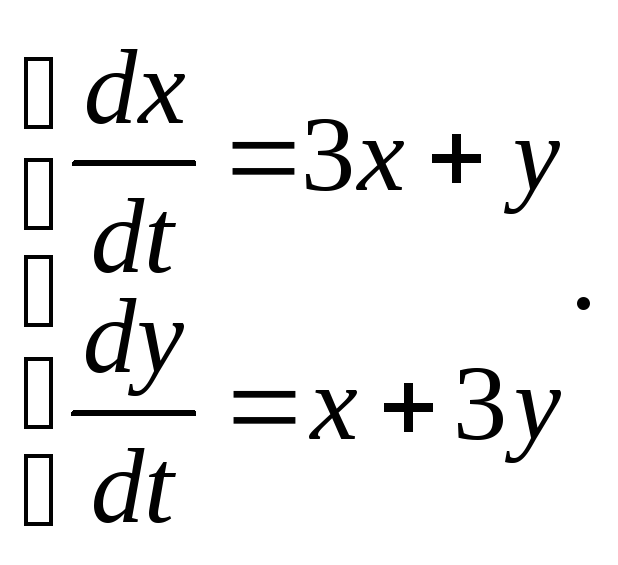
3.5.

3.6.

3.7.

3.8.

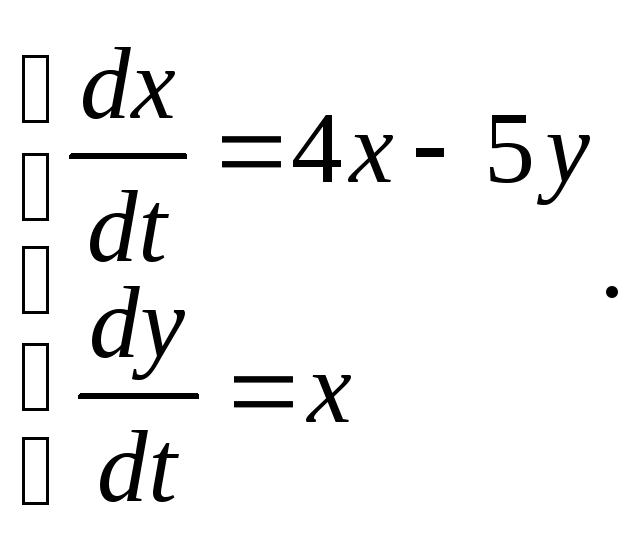
3.9.

3.10.

Контрольная работа № 6

«Ряды»

Задание 1. Исследовать числовой ряд на сходимость

1.1.	а) ;	б) ;	в) .
1.2.	а) ;	б) ;	в) .
1.3.	а) ;	б) ;	в) .
1.4.	а) ;	б) ;	в) .
1.5.	а) ;	б) ;	в) .
1.6.	а) ;	б) ;	в) .
1.7.	а) ;	б) ;	в) .
1.8.	а) ;	б) ;	в) .
1.9.	а) ;	б) ;	в) .
1.10.	а) ;	б) ;	в) .

Задание 2. Исследовать на абсолютную и условную сходимость знакочередующийся ряд

2.1.	.	2.2.	.	2.3.	.
2.4.	.	2.5.	.	2.6.	.
2.7.	.	2.8.	.	2.9.	.
		2.10.	.

Задание 3. Найти интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала сходимости

3.1.	.	3.2.	.	3.3.	.
3.4.	.	3.5.	.	3.6.	.
3.7.	.	3.8.	.	3.9.	.
		3.10.	.

Задание 4. Найти в виде степенного ряда решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. Ограничиться четырьмя членами ряда

4.1. .

4.2. .

4.3. .

4.4. .

4.5. .

4.6. .

4.7. .

4.8. .

4.9. .