Примеры для самостоятельного решения

Найти общие решения уравнений:

Решить задачу Коши:

1.7. Линейные дифференциальные уравнения n-го порядка.

Литература: [1], гл. I, §§ 1.15, 1.17

[3], гл. XIII, §§ 20, 23

[5], Ч. 2, гл. 11, §§ 11.6, 11.7

Линейным дифференциальным уравнением n-го порядка называется уравнение вида ,

где и− заданные функции, аy − искомая функция аргумента x. Функция y и ее производные входят в уравнение в первой степени, поэтому оно называется линейным. Функция f (x) называется правой частью уравнения.

Линейное дифференциальное уравнение называется однородным, если его правая часть . В противном случае уравнение называетсянеоднородным или уравнением с правой частью.

Однородное уравнение имеет очевидное решение . Но интерес представляет нахождение ненулевых решений.

Общее решение однородного уравнения n-го порядка по теореме о структуре общего решения однородного уравнения имеет вид , где− произвольные постоянные,− частные линейно независимые решения данного уравнения.

Напомним, что система непрерывных на отрезке функций называетсялинейно зависимой, если существуют числа , не все равные нулю, такие, что выполняется тождество. Если это тождество выполняется лишь в случае, когда всеравны нулю, то система функцийлинейно независима.

Линейную зависимость системы функций можно определить при помощи определителя Вронского (вронскиана):

Если функции y₁, y₂,…, y_n линейно зависимы на некотором промежутке, то в любой точке этого промежутка их вронскиан равен нулю. Если решения y₁, y₂,…, y_n линейного дифференциального однородного уравнения n-го порядка линейно независимы на некотором промежутке, то их вронскиан отличен от нуля в любой точке этого промежутка.

По теореме о структуре общего решения неоднородного уравнения общее решение неоднородного уравнения n-го порядка представляет собой сумму общего решения соответствующего однородного уравненияи частного решения неоднородного уравнения:.

Методы решения линейных дифференциальных уравнений рассмотрим на примере уравнений второго порядка.

1.8. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Литература: [1], гл. I, § 1.16

[3], гл. XIII, §§ 21

[5], Ч. 2, гл. 11, §§ 11.6

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами имеют вид

, где .

В соответствии с теоремой о структуре общего решения , где линейно независимые частные решенияинаходятся в зависимости от вида корней характеристического уравнения.

Характеристическим уравнением для линейного однородного дифференциального уравнения с постоянными коэффициентами называется алгебраическое уравнение, полученное из дифференциального уравнения заменой производных на k в степени, соответствующей порядку производных, и для уравнений второго порядка имеющее вид

.

Возможны три случая:

1) корни характеристического уравнения действительные и различные . В этом случае линейно независимыми частными решениями линейного однородного дифференциального уравнения являются функциии, а его общее решение имеет вид

, − произвольные постоянные.

2) корни характеристического уравнения действительные и равные . В этом случае линейно независимыми частными решениями линейного однородного дифференциального уравнения являются функциии, а его общее решение имеет вид

, − произвольные постоянные.

3) корни характеристического уравнения комплексные В этом случае линейно независимыми частными решениями линейного однородного дифференциального уравнения являются функции и, а его общее решение имеет вид

, − произвольные постоянные.

Пример 1. Решить уравнение .

Решение. Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Для его решения вначале составим характеристическое уравнение , корни которого действительные и различные,. Поэтому общее решение дифференциального уравнения имеет вид

, − произвольные постоянные.

Пример 2. Решить уравнение .

Решение. Составим характеристическое уравнение

Его можно представить в виде . Значит, корни характеристического уравнения действительные и равные. Поэтому общее решение дифференциального уравнения имеет вид

, − произвольные постоянные.

Пример 3. Решить задачу Коши для уравнения с начальными условиями.

Решение. Составим характеристическое уравнение . Его корни чисто мнимые. Отсюдаα=0 и β=2. Поэтому общее решение дифференциального уравнения имеет вид

.

Для определения ивоспользуемся начальными условиями. Предварительно найдем. Получим систему уравнений:

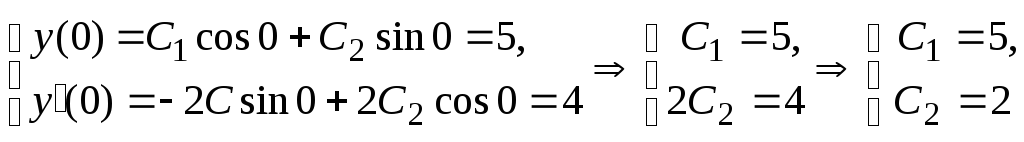
Решение задачи Коши, имеет вид .