2.3.3. Признак Даламбера

Если для положительного ряда существует предел вида, то этот ряд сходится прии расходится при. Припризнак Даламбера не решает вопроса о сходимости ряда.

Замечание. Признак Даламбера используют в том случае, если формула общего члена ряда содержит множитель или является показательной функцией отn.

Пример 1. Исследовать на сходимость ряд .

Решение. На возможность применения признака Даламбера указывает наличие в формуле общего члена множителей и.

Здесь . Для получениязаменим в формулевсеn на n+1. Получим . Тогда

.

По признаку Даламбера исследуемый ряд сходится.

Пример 2. Исследовать на сходимость ряд .

Решение. Здесь ,. Применяем признак Даламбера:

.

Ряд расходится.

Примеры для самостоятельного решения.

Исследовать на сходимость, пользуясь признаком Даламбера, следующие ряды:

а) ; б); в); г).

2.3.4. Радикальный признак Коши

Если для положительного ряда существует предел, то приl<1 данный ряд сходится, а при l>1 − расходится. При l=1 радикальный признак Коши, как и признак Даламбера, не дает ответа на вопрос о сходимости ряда.

На практике признак Коши применяется чаще всего, когда общий член ряда представляет собой показательную или показательно-степенную функцию от n.

Пример 1. Исследовать на сходимость ряд

.

Решение. Общий член ряда содержит выражение в степени n. Поэтому целесообразно воспользоваться радикальным признаком Коши:

.

Исследуемый ряд сходится.

Пример 2. Исследовать на сходимость ряд .

Решение. Вычислим предел

,

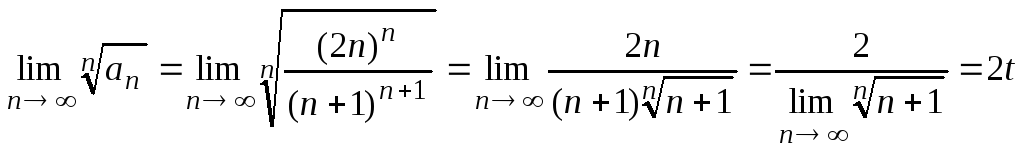где .

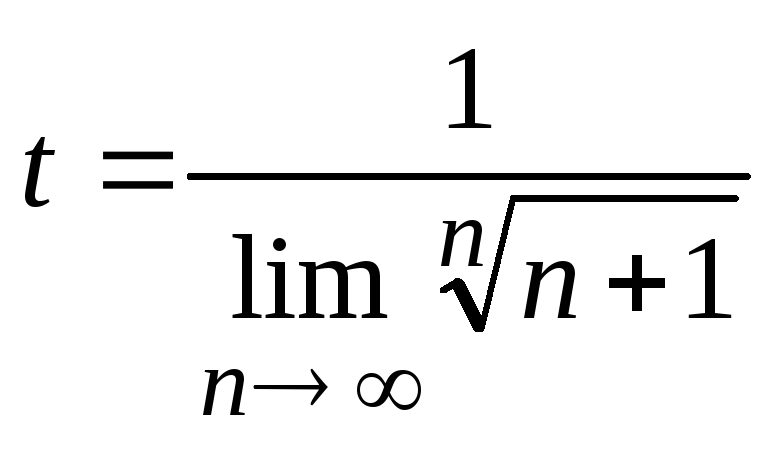Для вычисления этого предела воспользуемся правилом Лопиталя, предварительно прологарифмировав полученное выражение:

.

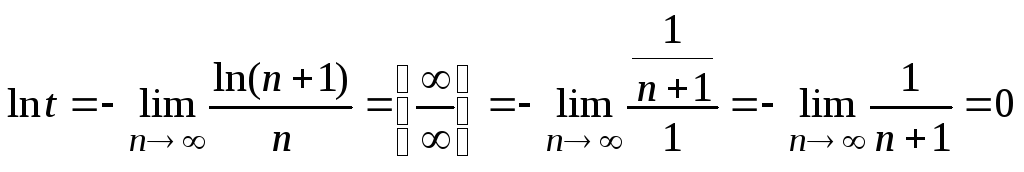Так как lnt=0, то t=1, и, следовательно, .

Так как , то по радикальному признаку Коши ряд расходится.

Примеры для самостоятельного решения

Исследовать на сходимость при помощи радикального признака Коши следующие ряды:

а) ; б); в); г).

2.3.5. Интегральный признак Коши

Пусть общий член ряда представляет собой значение функции при, т.е.. Если при этом функциямонотонно убывает в некотором промежутке, где, то данный ряд сходится, если сходится несобственный интеграл, и расходится, если этот несобственный интеграл расходится. Из этой теоремы вытекает важное для практики следствие: для сходящегося ряда с общим членом, удовлетворяющим условиям теоремы, остаток ряда можно оценить из соотношения.

Рассмотрим примеры применения интегрального признака Коши.

Пример. Исследовать на сходимость ряд .

Решение. Так как является значением функцииприи эта функция непрерывна и монотонно убывает в промежутке, то исследуем на сходимость несобственный интеграл

.

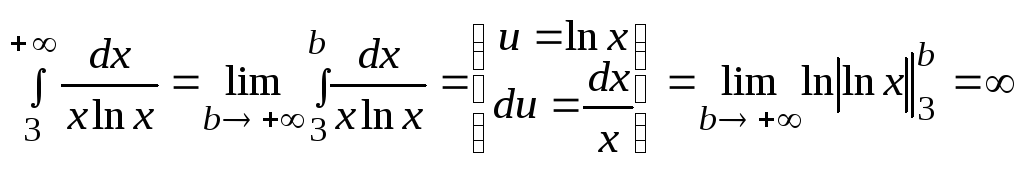Интеграл расходится. Следовательно, расходится и данный ряд.

Примеры для самостоятельного решения.

Исследовать на сходимость при помощи интегрального признака Коши следующие ряды:

а) ; б); в); г).

2.4. Сходимость и расходимость знакопеременных рядов

Литература: [5], Ч. 3, гл. 15, § 15.4

Ряд с членами произвольных знаков называется знакопеременным. В дальнейшем будут рассматриваться ряды с бесконечным числом положительных и отрицательных членов.

Знакопеременный ряд называетсяабсолютно сходящимся, если сходится ряд, составленный из модулей его членов .

Теорема об абсолютной сходимости ряда: если сходится ряд, составленный из модулей членов данного ряда, то данный знакопеременный рядтакже сходится (т.е. является абсолютно сходящимся).

Ряд называетсяусловно сходящимся, если он сходится, а ряд, составленный из модулей его членов , расходится.

Основные свойства абсолютно и условно сходящихся рядов:

1) абсолютно сходящийся ряд остается сходящимся и не меняет величины суммы при любой перестановке его членов;

2) изменяя порядок следования членов в условно сходящемся ряде, можно сделать сумму ряда равной любому наперед заданному числу или даже сделать ряд расходящимся;

3) если знакопеременный ряд сходится абсолютно, то сходятся ряды составленные только из его положительных или только отрицательных членов; если же ряд сходится условно, то упомянутые выше ряды сходятся.

Пример 1. Исследовать на абсолютную и условную сходимость ряд

Решение. Ряд знакочередующийся, в связи с ростом знаменателя его членов последние убывают по абсолютной величине. Легко видеть, что предел общего члена ряда при n→∞ равен нулю: . Значит, по признаку Лейбница данный знакочередующийся ряд сходится.

Рассмотрим теперь ряд, составленный из модулей его членов,

Это гармонический ряд, который, как известно, расходится. Следовательно, данный ряд − условно сходящийся.

Пример 2. Исследовать на абсолютную и условную сходимость ряд

Решение. Данный ряд знакопеременный, так как может принимать как положительные, так и отрицательные значения. Рассмотрим ряд, составленный из модулей членов данного ряда:

Ввиду очевидного неравенства по признаку сравнения для положительных рядов имеем, что рядсходится, т.к. сходится ряд. Из сходимости рядапо признаку абсолютной сходимости имеем, что рядсходится и притом абсолютно.