§4. Розкриття невизначеностей.

Правило Бернуллі-Лопиталя

I Поняття невизначеного виразу

Нехай і – нескінченно малі, а й – нескінченно великі функції при .

Невизначеними виразами (або невизначеностями) при називають наступні вирази:

1) – невизначеність виду ;

2) – невизначеність виду ;

3) – невизначеність виду ;

4) – невизначеність виду ;

5) – невизначеність виду ;

6) – невизначеність виду ;

7) – невизначеність виду .

Розкрити невизначеність означає обчислити границю (відповідного виразу) за умови, що .

II Невизначеності виду , .

Теорема Бернуллі-Лопиталя. Нехай функції й задовольняють умовам: 1) визначені й диференційовані на ; 2) ; 3)вираз є при невизначеністю виду або . Тоді, якщо існує границя (скінчена або нескінчена), то існує й границя , причому справедлива формула

.

Іншими словами, границю відношення двох н.м. або н.в. функцій можна замінити границею відноношення їхніх похідних, якщо остання існує – це і є правило Бернуллі-Лопиталя.

Доведення. Доведемо теорему лише для випадку . Довизначемо функції й у точці , поклавши їх рівними нулю: . Тепер ці функції неперервні на всьому замкнутому проміжку : їхнє значення в точці а збігаються з границями (адже й при ), в інших же точках неперервність випливає з диференційованості. До цієї пари функцій можемо застосувати теорему Коші з §3:

,

де . З огляду на, що функції в точці а дорівнюють нулю, одержимо

.

Очевидно, що при й . Права частина останньої рівності має при границю (за умовою теореми), але тоді й ліва частина має ту ж саму границю.

Зауваження 1. Аналогічне твердження має місце й для лівої границі, а також для границь на нескінченності, тобто при .

Приклад 1. Для . Цією границею доведено, нарешті, співвідношення , тобто при ( ).

Зауваження 2. Якщо похідні й задовольняють тим же вимогам, що й самі функції й , то правило Бернуллі-Лопиталя можна застосувати повторно.

Приклад 2. .

Неважко помітити, що

.

Інакше кажучи, або при .

Зауваження 3. Правило Бернуллі-Лопиталя можна застосовувати тільки, коли границя відношення похідних існує. Наприклад,

,

але не існує. Цей приклад показує, що з не-існування не можна робити висновку про

Зауваження 4. Існують ситуації, у яких застосування правила Бернуллі-Лопиталя нічого не дає.

Приклад 3. .

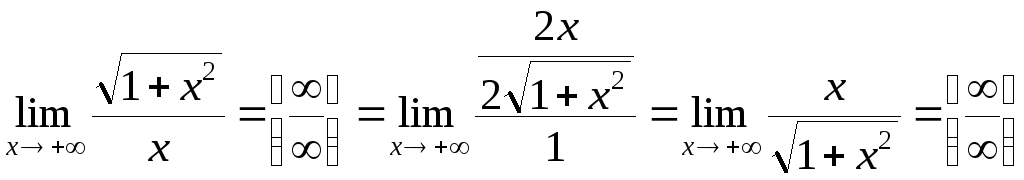Ще одне застосування правила поверне нас до початкової границі.

III Інші види невизначеностей.

Ще раз нагадаємо, що правило Бернуллі-Лопиталя можна застосовувати лише до невизначеностей виду й . Всі інші невизначеності необхідно зводити до однієї із цих двох шляхом алгебраїчних перетворень.

А) . Тому що , то цю невизначеність можна звести до або .

Приклад 4. Для :

.

Помітимо, що, якщо інакше перетворити добуток у частку, то застосування правила Бернуллі-Лопиталя приводить до ускладнення невизначеності: .

B) . Тому що ,то дана невизна-ченість зводиться до виду . Часто, втім, того ж вдається досягти простіше.

Приклад 5.

Обчислення можна спростити, якщо перед першим застосуванням правила використати еквівалентність , :

.

С) , , . Тому що (основна логарифмічна тотожність) і (неперервність показникової функції), то невизначеності цих типів зводяться до невизначеності виду .

Приклад 6. (дивися приклад 4).

Приклад 7.

(дивися приклад 1).

Зауваження 5. Розкриваючи невизначеності за правилом Бернуллі-Лопиталя, доцільно використовувати й інші методи обчислення границь: еквівалентності, заміна змінної й т.д.

Приклад 8.

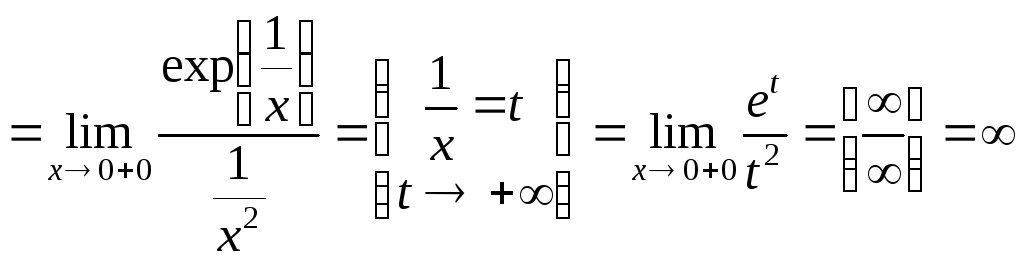(дивися приклад 2).