III Таблиця диференціалів

Диференціал dy лише множником dx відрізняється від похідної , тому по таблиці похідних легко скласти таблицю диференціалів.

1. , , .

2. , .

3. , .

4. . 5. .

6. . 7. .

8. . 9. .

10. . 11. .

Також легко одержати формули для диференціалів суми, різниці, добутку й частки функцій:

а)

б)

в)

Відзначимо, що в таблиці диференціалів змінна x може бути як незалежною, так і деякою функцією. У таблиці ж похідних (§6) x – це тільки незалежна змінна.

Зауваження. Формула для диференціала функції , а саме: , дозволяє написати формулу, що виражає похідну функції через диференціали аргументу і функції d x і dy:

.

При цьому така формула зберігає силу, незалежно від того по якій змінній були у обчислені dx і dy. Ця формула дозволяє легко запам'ятовувати (але не доводити!) деякі правила диференціювання:

для складної функції

;

для оберненої функції

;

для функції, заданої параметрично

.

§8. Похідні вищих порядків

I Означення й позначення

Якщо функція диференційована на деякому проміжку, то її похідна сама є функцією, визначеною на цьому проміжку. Отже, стосовно неї можна порушувати питання про існування й знаходження похідної. Якщо вона існує, то її називають другою похідною (або похідною 2^го порядку), і позначають одним із символів

.

Аналогічно, якщо існує похідна від другої похідної, те її називають третьою похідною і позначають, наприклад, .

Взагалі, похідною n-го порядку називають похідну від похідної (n–1)-го порядку й позначають . Отже, за означенням

.

II Похідні деяких функцій

1. y=sinx, y=cosx

Перші похідні цих функцій і формули приведення дозволяють методом математичної індукції одержати вирази для похідних n-го порядку:

.

2. y=x^

Якщо , то, послідовно диференціюючи, одержимо , , і взагалі:

.

Якщо ж показник степеня натуральний, то:

3. y=a^x

, зокрема, , .

4. y=lnx

,

.

III Деякі правила

Очевидно, що й . Для похідної

n-го порядку від добутку функцій є т.зв. формула Лейбниця. Приведемо її без доведення

, де .

Помітимо, що під похідною нульового порядку прийнято розуміти саму функ-цію: .

IV Функція, що дана параметрично

Нехай функція задана параметричними рівняннями

Її перша похідна – це також функція,яка задана параметрично:

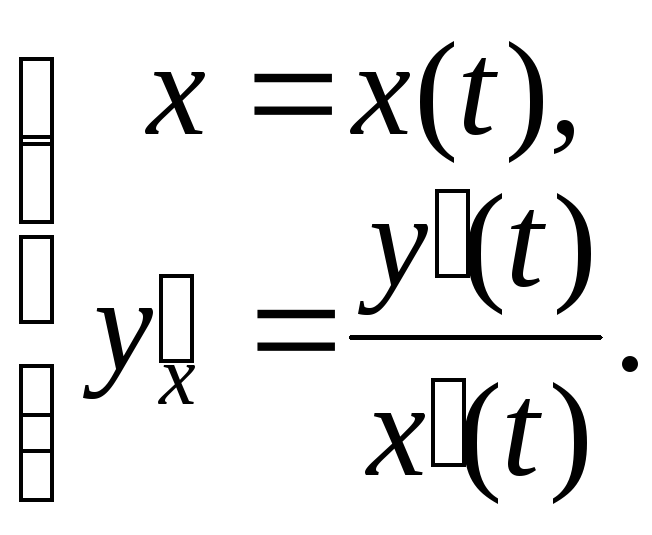
Тоді

Приклад. Для перша похідна має вигляд Тоді й друга похідна така:

V Функція, що дана неявно

Повторне диференціювання такої функції покажемо на прикладі:

Тоді за означенням:

.

Залишається підставити в останній вираз значення :

.

Отриманий вираз можна спростити, використовуючи саме рівняння:

.

Тема ОСНОВНІ ТЕОРЕМИ ПРО

Диференційовані функції

Лекція 10

§1. Необхідна умова экстремуму

Розглянемо функцію , яка визначена на проміжку , і нехай точка – внутрішня точка проміжку: .

Означення 1. Точка називається точкою (локального) максимуму функції , якщо існує окіл цієї точки, у якому (при ) виконується нерівність . Іншими словами, для малих приростів аргументу приріст функції .

Означення 2. Точка називається точкою (локального) мінімуму функції , якщо існує окіл цієї точки, у якому (при ) виконується нерівність . Іншими словами, при малих .

Точки максимуму й мінімуму називаються точками екстремуму. Їх можна характеризувати в такий спосіб: приріст функції в точці екстремуму має постійний знак, що не залежить від знака (якщо достатньо мало).

Теорема Ферма. Якщо функція диференційована в точці й має в цій точці локальний екстремум, то .

Доведення. Диференційованість означає існування скінченої границі

.

Для цієї границі є три можливості: 1) ; 2) ; 3) . Припустимо, що . Тоді для близьких до нуля різницеве відношення . Якщо ж , то й (для малих ). В обох випадках знак залежить від знака . Але за умовою теореми – це точка екстремуму, виходить, знак не залежить від знака . Це протиріччя означає, що не може бути ні додатним, ні від‘ємним. Залишається остання можливість: .

Зауваження 1. Ця теорема має простий геометричний зміст: якщо в точці графіка функції , який відповідає екстремум функції, існує дотична до графіка, то ця дотична паралельна осі Ox.

Зауваження 2. Сформульована в теоремі умова є необхідна, але не достатня. Наприклад, функція має похідну , що стає нулем у точці . Однак,

.

Вираз в дужках завжди додатний, як неповний квадрат суми. Отже, і в точці немає екстремуму.