X Диференціювання функції, даної неявно

При деяких умовах, які будуть сформульовані в темі “Функції декількох змінних”, рівняння із двома змінними виду визначає y як функцію від x: . Інакше кажучи, існує функція, щоперетворює рівняння в тотожність. Похідну цієї функції можна знайти (у неявному ж вигляді), не знаходячи самої функції. Точні формули будуть дані пізніше, а зараз сформулюємо правило:

тотожність диференціюємо поx, не забуваючи, що y – це функція від x; потім з отриманої рівності знаходимо .

Приклади. 4. Дано: . Диференціюємо поx обидві частини:

. .

5. Виведемо рівняння дотичної до еліпса , що проходить через йоготочку . Знайдемо кутовий коефіцієнт дотичної. Дляцього рівняння еліпса диференціюємо по x, не забуваючи, що :

.

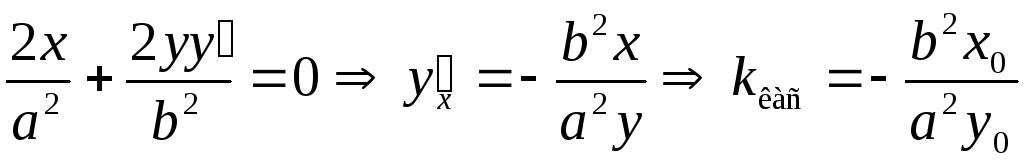У загальне рівняння дотичної підставимо знайдений коефіцієнт і перетворимо рівняння:

.

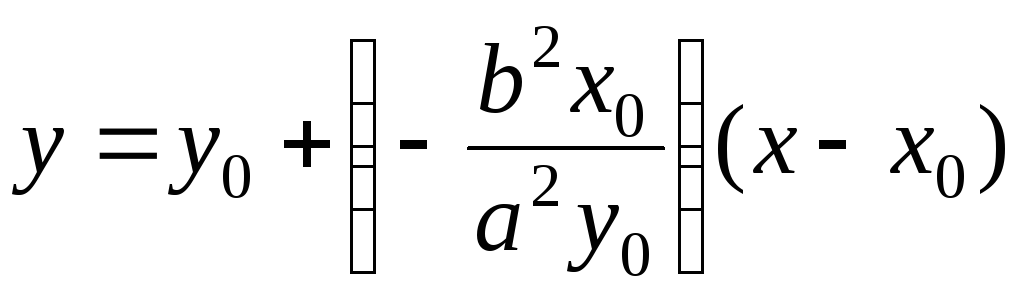
Через те, що точка належитьеліпсу, права частина отриманого рівняння дорівнює 1. Отже, шукана дотична має рівняння

.

§7. Диференціал функції

I Означення й геометричний зміст

Відомо, що приріст диференційованої у точці функціїможна записати у вигляді сумидвох доданків, кожен з яких наближається до нуля при . Однак, другий доданок має порядок малостібільш високий, чим перший (“швидше” наближається до нуля). Тобто в цій сумі головну роль грає перший доданок.

Означення. Головна частина приросту функції, лінійна щодоприросту аргументуx, називається диференціалом функції й позначається символом dy.

Отже,

.

Геометричний зміст бачимо з малюнка: диференціал функції – це приріст ординати дотичної до графіка функції, що відповідає приросту аргументу .

Диференціалом незалежної змінної x, прийнято називати її приріст і позначатиdx: . Тоді формула для диференціала функціїздобуває симетричний вигляд

або .

II Інваріантність форми першого диференціала

Правило диференціювання складної функції приводить до однієї дуже важливої властивості диференціала. Обчислимо dy для функції у двох випадках:

1) x – незалежна змінна, тоді ;

2) x – деяка функція , тоді

Порівнюючи результати, одержуємо т.зв. властивість інваріантності форми першого диференціала:

форма 1^го диференціала функції не залежить від того,є змінна x незалежною або функцією іншої змінної.

III Таблиця диференціалів

Диференціал dy лише множником dx відрізняється від похідної , тому потаблиці похідних легко скласти таблицю диференціалів.

1. ,,.

2. ,.

3. ,.

4. . 5..

6. . 7..

8. . 9..

10. . 11..

Також легко одержати формули для диференціалів суми, різниці, добутку й частки функцій:

а)

б)

в)

Відзначимо, що в таблиці диференціалів змінна x може бути як незалежною, так і деякою функцією. У таблиці ж похідних (§6) x – це тільки незалежна змінна.

Зауваження. Формула для диференціала функції , а саме:, дозволяє написати формулу, що виражає похідну функції через диференціали аргументу і функціїd x і dy:

.

При цьому така формула зберігає силу, незалежно від того по якій змінній були у обчислені dx і dy. Ця формула дозволяє легко запам'ятовувати (але не доводити!) деякі правила диференціювання:

для складної функції

;

для оберненої функції

;

для функції, заданої параметрично

.