§5. Основні правила диференціювання

I. Якщо , то (похідна постійної функції дорівнює 0).

II. Якщо , а – диференційована в точці x, то (постійний множник можна винести за знак похідної).

III–V. Якщо функції й диференційовані в точці x, то їхня сума, різниця, добуток і частка (якщо ) також диференційовані в цій точці, причому мають місце формули:

III.

IV.

V.

Доведемо, наприклад, формулу диференціювання частки. Нехай . Тоді:

.

Додамо й віднімемо в чисельнику член , згрупуємо й винесемо за дужки загальні множники. Будемо мати:

.

Складемо різницеве відношення, тобто відношення приросту функції до приросту аргументу:

.

Тепер перейдемо до границі при . Через те, що й – диференційовані (а, отже, неперервні), то існують границі

, , ,

а й від не залежать і виносяться за знаки границь. Виходить, існує границі різницевого відношення, тобто

.

VI. Нехай функція диференційована в точці , а функція диференційована в точці , причому . Тоді й складна функція диференційована в точці й має місце формула

.

Інші форми запису цієї формули:

, .

Для доведення надаємо аргументу x функції приріст . Він викличе приріст цієї функції, що у свою чергу викличе приріст функції . Внаслідок теореми 1 §4 з диференційованості функцій і маємо:

Підставляючи першу формулу в другу, одержимо для приросту складної функції:

Відразу відзначимо, що внаслідок неперервності функції (випливає з її диференційованості) її приріст прагне до нуля при . Складаємо різницеве відношення й переходимо до границі

.

Перший доданок під знаком границі в правій частині – це постійна. Другий – добуток постійної на нескінченно малу, тому що за означенням символу . Третій доданок запишемо у вигляді

.

Тут перший множник є нескінченно мала при , а другий має скінчену границю . Отже, другий і третій доданок – це нескінченно малі при . Звідси й одержуємо формулу диференціювання складної функції.

Зауваження 1. Інші правила диференціювання приведемо пізніше.

§6. Похідні основних елементарних функцій

I Степенева функція y=x^

Знаходимо приріст функції й складаємо різницеве відношення:

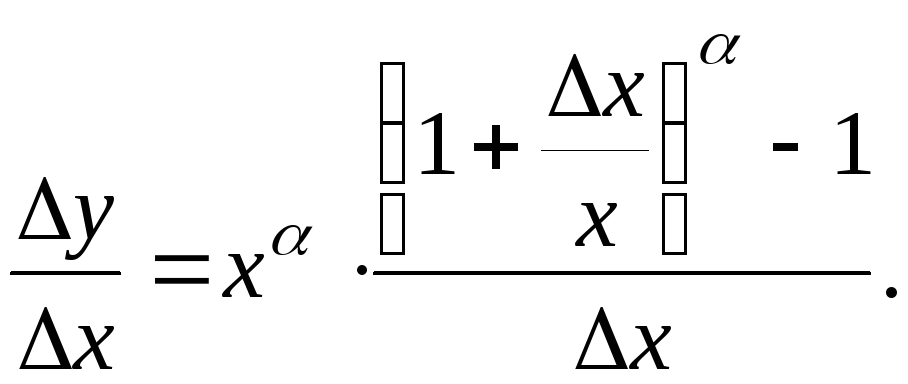
Обчислимо границю цього різницевого відношення, використовуючи еквівалентність для степеневої функції  m при :

Отже, маємо

(1)

Зауваження 1. Виведення останньої формули припускає, що . Обчислимо (вважаємо, що , отже, ):

.

Величина цієї границі залежить від : для , для й для . Але цей же результат можна одержати з формули (1) за допомогою теореми 2 §3. Аналогічний результат можна одержати й для , якщо  таке, що степенева функція визначена для .

Зауваження 2. Ряд окремих випадків формули (1) краще запам'ятати як самостійні формули диференціювання:

, , .

II Показникова функція y=a^x

.

Отже,

.

Окремий випадок цієї формули: .

III Логарифмічна функція

Отже,

.

Для логарифмічної функції з довільною основою використовуємо формулу перехіду:

.

Звідси .

Можна запропонувати й інший спосіб обчислення з використанням основної логарифмічної тотожності . Здиференціював почленно цю тотожність, одержимо:

.

Звідси й одержимо .