IX Дифференцирование функции, заданной параметрически

Пусть имеется система параметрических уравнений ,, причем функцииидифференцируемы исохраняет знак. Тогда на области значений функциисуществует дифференцируемая функция, причем

Действительно, из условия (или) следует монотонность функции; следовательно, у неё существует обратная. Тогда– некоторая функция отx. Её производную можно найти, если применить правила дифференцирования сложной и обратной функций:

Пример. 3. Составим уравнение касательной к эллипсув точке, соответствующей значению параметра.

Координаты точки касания: ,. Угло-

вой коэффициент касательной

.

Искомое уравнение имеет вид: .

Замечание 3.Вообще говоря, производная функции, заданной параметрически, есть функция, заданная параметрически. Методически более правильным было бы писать такую производную в виде системы параметрических уравнений:

X Дифференцирование функции, заданной неявно

При некоторых условиях, которые будут сформулированы в теме “Функции нескольких переменных”, уравнение с двумя переменными вида определяетy как функцию отx:. Другими словами, существует функция, обращающая уравнение в тождество. Производную этой функции можно найти (в неявном же виде), не находя самой функции. Точные формулы будут даны позже, а сейчас сформулируем правило:

тождество дифференцируем поx, не забывая, чтоy– это функция отx; затем из полученного равенства находим.

Примеры.4. Дано: . Дифференцируем поxобе части:

..

5. Выведем уравнение касательной к эллипсу , проходящей через его точку. Найдем угловой коэффициент касательной. Для этого уравнение эллипса дифференцируем поx, не забывая, что:

.

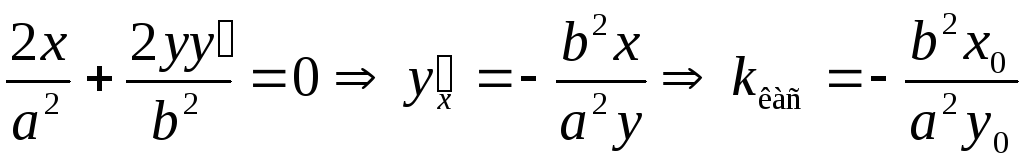В общее уравнение касательной подставим найденный коэффициент и преобразуем уравнение:

.

Так как точка принадлежит эллипсу, то правая часть полученного уравнения равна1. Следовательно, искомая касательная имеет уравнение

.

§7. Дифференциал функции

I Определение и геометрический смысл

Известно, что приращение дифференцируемой в точке функцииможно записать в виде суммы

двух слагаемых, каждое из которых стремится к нулю при . Однако, второе слагаемое имеет порядок малости более высокий, чем первое (“быстрее” стремится к нулю). То есть в этой сумме главную роль играет первое слагаемое.

Определение.Главная часть приращенияфункции, линейная относительно приращенияаргументаx, называется дифференциалом функ-ции и обозначается символомdy.

Итак,

.

Геометрический смысл виден из рисунка: дифференциал функции – это приращение ординаты касательной к графику функции, соответствующее приращению аргумента .

Дифференциалом независимой переменной x, принято называть ее приращениеи обозначатьdx:. Тогда формула для дифференциала функции приобретает симметричный вид

или.

II Инвариантность формы первого дифференциала

Правило дифференцирования сложной функции приводит к одному очень важному свойству дифференциала. Вычислим dyдля функциив двух случаях:

1) x– независимая переменная, тогда;

2) x– некоторая функция, тогда

Сравнивая результаты, получаем т.н. свойство инвариантности формы первого дифференциала:

форма 1^годифференциала функциине зависит от того, является

ли переменная x независимой или функцией другой переменной.