IV Тригонометрические функции

1. y=sinx

.

(на последнем шаге мы воспользовались непрерывностью косинуса).

Итак,

.

Производные остальных тригонометрических функций можно вычислить, используя определение производной, но проще использовать известные правила дифференцирования и формулы, связывающие тригонометрические функции друг с другом.

2. y=cosx

.

Итак,

.

3. y=tgx

.

Итак,

.

4. y=сtgx.

Аналогично предыдущему можно получить

(ctg.

V Обратные тригонометрические функции

Производные этих функций проще всего получить при помощи основного тождества, связывающего пару взаимно обратных функций, а именно: .

1. y=arcsinx

Дифференцируем почленно тождество :

(напомним, что , поэтому).

Итак,

.

2. y=arccosx

Известное соотношение и предыдущая формула для, позволяют получить

.

3. y=arctgx

Итак,

.

4. y=arcctgx

Из соотношения , получим

.

Замечание 3.Покажем на примерекак можно получать производные аркфункций, исходя из определения производной. Приращение арктангенсастремится к0при(в силу непрерывности функции). Отсюда получаем эквивалентность: приТеперь можно легко найти предел разностного отношения:

.

Замечание 4.Производные аркфункций можно получить также, используя общее правило дифференцирования обратной функции, которое будет приведено ниже.

VI Гиперболические и обратные гиперболические функции

Эти функции элементарным образом выражаются через показательную и логарифмическую функции. Поэтому проще всего находить их производные, используя известные правила дифференцирования.

Например:

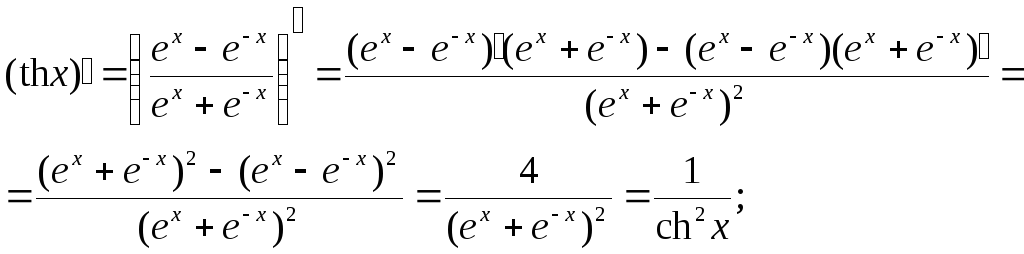
Производные других функций этой группы студентам предлагается получить самостоятельно.

VII Сводка формул для производных

1.,,,.

2.,.

3.,.

4.. 5..

6.(tg. 7. (ctg.

8..9..

10..11..

12..13..

14..15..

16..

17..

18..

§5 (Продолжение). Основные правила дифференцирования

VII Логарифмическая производная

Пусть функция положительна и дифференцируема. Тогда и функция– дифференцируема, причем

.

Это выражение и называется логарифмической производной функции . Отсюда легко получить производную самой функции:

.

Используя эту формулу можно получить правило дифференцирования сложной степенно-показательной функции:

.

Окончательно имеем формулу:

.

Замечание 2.Вообще говоря, всегда лучше помнить не лишнюю формулу, а приём, который приводит к этой формуле. Для степенно-показательной функции можно предложить прием, использующий основное логарифмическое тождество:

.

Примеры.

2.

VIII Дифференцирование обратной функции

Пусть функция в некоторой окрестности точки– непрерывная и строго монотонная, а кроме того, дифференцируема в точке, причем. Тогда в некоторой окрестности точкисуществует обратная функция, также непрерывная, строго монотонная и дифференцируемая в точке, причем

. (1)

Строгое доказательство приводить не будем, но дадим геометрическую иллюстрацию. При этом используем тот факт, что у графики взаимно-обратных функций исовпадают, а производная – это угловой коэффициент касательной.

,

Формулу (1) записывают еще в виде или.

Применим последнюю формулу для вычисления производной, например, арксинуса:

,