§5. Основные правила дифференцирования

I.Если, то(производная постоянной функции равна 0).

II.Если, а– дифференцируема в точкеx, то(постоянный множитель можно вынести за знак производной).

III–V.Если функцииидифференцируемы в точкеx, то их сумма, разность, произведение и частное (если) также дифференцируемы в этой точке, причем имеют место формулы:

III.

IV.

V.

Докажем, например, формулу дифференцирования частного. Пусть . Тогда:

.

Добавим и вычтем в числителе член , сгруппируем и вынесем за скобки общие множители. Будем иметь:

.

Составим разностное отношение, т.е. отношение приращения функции к приращению аргумента:

.

Теперь перейдем к пределу при . Так каки- дифференцируемы (а, следовательно, непрерывны), то существуют пределы

,,,

а иотне зависят и выносятся за знаки пределов. Значит, существует предел разностного отношения, т.е.

.

VI.Пусть функциядифференцируема в точке, а функциядифференцируема в точке, причем. Тогда и сложная функциядифференцируема в точкеи имеет место формула

.

Другие формы записи этой формулы:

,.

Для доказательства придаем аргументу xфункцииприращение. Оно вызовет приращениеэтой функции, которое в свою очередь вызовет приращениефункции. В силу теоремы 1§4из диффе-ренцируемости функцийиимеем:

Подставляя первую формулу во вторую, получим для приращения сложной функции:

Сразу отметим, что в силу непрерывности функции (следует из её дифференцируемости) ее приращениестремится к нулю при. Составляем разностное отношение и переходим к пределу

.

Первое слагаемое под знаком предела в правой части – это постоянная. Второе – произведение постоянной на бесконечно малую, ибо по определению символа. Третье слагаемое представим в виде

.

Здесь первый множитель есть бесконечно малая при , а второй имеет конечный предел. Итак, второе и третье слагаемое – это бесконечно малые при. Отсюда и получаем формулу дифференцирования сложной функции.

Замечание 1.Остальные правила дифференцирования приведем позже.

§6. Производные основных элементарных функций

I Степенная функция y=x^

Находим приращение функции и составляем разностное отношение:

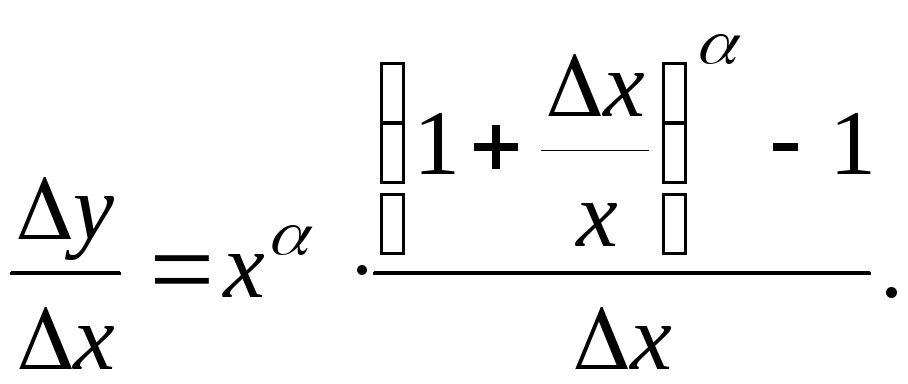
Вычислим предел этого разностного отношения, используя эквивалентность для степенной функции  m при:

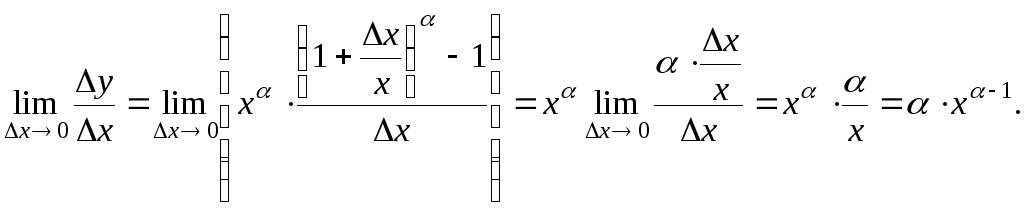Итак, имеем

(1)

Замечание 1.Вывод последней формулы предполагает, что. Вычис-лим(считаем, что, следовательно,):

.

Величина этого предела зависит от : для, дляи для. Но этот же результат можно получить из формулы (1) с помощью теоремы 2§3. Аналогичный результат можно получить и для, еслитаково, что степенная функция определена для.

Замечание 2.Ряд частных случаев формулы (1) лучше запомнить как самостоятельные формулы дифференцирования:

,,.

II Показательная функция y=a^x

.

Итак,

.

Частный случай этой формулы: .

III Логарифмическая функция

Итак,

.

Для логарифмической функции с произвольным основанием используем формулу перехода:

.

Отсюда .

Можно предложить и другой способ вычисления с использованием основного логарифмического тождества. Продифференцировав почленно это тождество, получим:

.

Отсюда и получим .