Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

KonspektElektrotekhnika_i_elektronika

.pdf

Скачиваний:

Добавлен:

03.03.2016

Размер:

6.68 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

Электротехника и электроника

1.8. ПРИМЕНЕНИЕ ЗАКОНОВ КИРХГОФА ДЛЯ РАСЧЕТОВ СЛОЖНЫХ ЦЕПЕЙ

При помощи первого и второго законов Кирхгофа можно найти токи во всех ветвях разветвленной цепи с произвольным числом источников энергии, если заданы ЭДС всех источников и сопротивления всех участков цепи. Для этого:

1.Произвольно намечают на схеме стрелками направления искомых токов,

которые называют положительными направлениями.

2.Число неизвестных токов равно числу ветвей n цепи. Составляют систе- му уравнений, в которой:

- число уравнений, составленных по первому закону Кирхгофа, должно быть на единицу меньше числа узлов цепи (m - 1);

- недостающие уравнения n – (m-1) должны быть составлены по второму закону Кирхгофа. Каждый следующий контур, для которого пишется уравне- ние, должен содержать хотя бы одну ветвь, не вошедшую в уже обойденные контуры.

3.Решая полученную систему уравнений, находят все токи. Те из них, дей- ствительные направления которых отличны от намеченных, получат при реше- нии отрицательные числовые значения.

4.По действительным направлениям токов определяют режимы работы ис- точников.

5.Определяют мощности, генерируемые и потребляемые элементами цепи. Баланс мощностей должен сходиться.

Например, цепь, представленная на рис.1.28, содержит пять ветвей n = 5. Таким образом, имеем пять неизвестных токов.

Так как цепь имеет три узла m= 3, то по первому закону Кирхгофа для нее

I1	R1	a I2	R2		R3	I3	должно быть составлено:
I1	R1	a I2	R2	b	R3	I3	(m-1) = 3 - 1 = 2 два уравнения,
		I5		I4			а по второму:
Е1		I5		I4		Е2	n - (m - 1) = 5 - (3 - 1) = 3 - осталь-
		R		R4			ные три уравнения.
	R01	5			R02		По первому закону Кирхгофа по-
	R01				R02		По первому закону Кирхгофа по-
		c		c			лучим:
		c		c			для узла а: I1 + I2 - I5= 0;
							для узла а: I1 + I2 - I5= 0;
		Рис. 1.28					для узла b: I3 - I2 - I4 = 0.
							В качестве контуров для приме-
нения второго закона Кирхгофа выберем те три ячейки, на которые ветвями ас
и bс разбивается весь внешний контур цепи. Обходя ячейки по направлению
движения часовой стрелки, получим:
для левой ячейки:			E1 = (R01 + R1) I1 + R5I5;
для средней ячейки, в которой нет источников энергии:

0 = - R2I2 + R4I4 – R5 I5;

для правой ячейки: - E2 = - (R02 + R3) I3 – R4 I4.

Решая полученную систему уравнений, можно найти все пять токов.

- 20 -

2. Однофазные электрические цепи

2.ОДНОФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ПЕРЕМЕННОГО ТОКА

2.1. ПОЛУЧЕНИЕ СИНУСОИДАЛЬНОЙ ЭДС

Электрические цепи, в которых величины и направления ЭДС, напряжения и тока периодически изменяются во времени по синусоидальному закону, на-

зываются цепями синусоидального переменного тока. Преимущества синусоидальных токов

1)возможность при помощи трансформаторов повышать и понижать напряже- ние для передачи энергии на большие расстояния;

2)простота устройства и меньшая стоимость электродвигателей переменного тока.

							Для получения			синусоидаль-
		N					ной ЭДС служат генераторы пере-
		N				ω	менного тока, в основе работы ко-
							менного тока, в основе работы ко-
					b		торых	лежит закон		электромаг-
					b		торых	лежит закон		электромаг-
		a	e	i			нитной	индукции. Явление элек-
		a	e				тромагнитной индукции заключа-
		щ1			e		тромагнитной индукции заключа-
EL	u	щ1			e		ется в	том,	что при		изменении
EL	u	i			c		ется в	том,	что при		изменении
		i			c		магнитного		потока	Ф,	пронизы-
		d					магнитного		потока	Ф,	пронизы-
		d					вающего замкнутый			проводящий
	i	+ щ2					вающего замкнутый			проводящий
	i						контур, в этом контуре наводится
		S					(индуктируется) ЭДС.
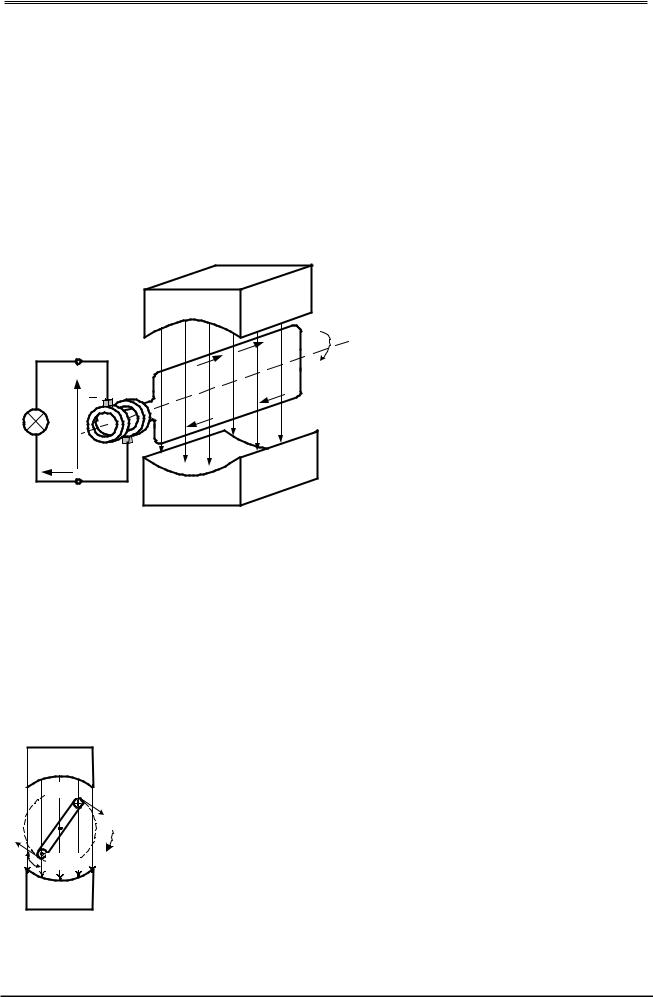
							На рис. 2.1 изменение магнит-
		Рис. 2.1					ного потока сквозь контур проис-
		Рис. 2.1					ходит благодаря движению про-
							ходит благодаря движению про-
							водников рамки abcd в магнитном
поле между полюсами постоянного магнита (N – северный , S - южный).
	Рамка вращается с постоянной угловой скоростью ω . Провода рамки ab и
cd (длиной l) пересекают силовые линии магнитного поля. В них наводится
ЭДС, величина которой пропорциональна магнитной индукции В, длине про-
водника l, скорости перемещения проводника в магнитном поле v и синусу угла
α между направлением магнитного поля и направлением движения проводника
(рис. 2.2):

N
eab	v
	v
v

α	ecd ω
B	S

Рис. 2.2

e = B·l·v·sin α,

где произведение v·sinα определяет нормальную к направле- нию поля составляющую скорости.

С учетом двух проводников ЭДС контура: e = 2 B·l·v·sin α = Em sin α,

где Em= 2 B·l·v - максимальное значение ЭДС.

Для определения направления индуктированной ЭДС ис- пользуется правило правой руки: если расположить правую руку так, чтобы магнитные линии входили в ладонь, а отстав- ленный на 90º большой палец указывал направление движения проводника, то вытянутые четыре пальца укажут направление

- 21 -

Электротехника и электроника

индуктированной ЭДС.

ЭДС е = 0, когда α = 0º, т.е. плоскость рамки перпендикулярна линиям маг- нитной индукции (горизонтальное положение). ЭДС принимает максимальное значение Em, когда α = 90º, т.е. плоскость рамки совпадает с осью магнитного поля (вертикальное положение - рис. 2.1).

Угол α изменяется во времени и равен произведению угловой скорости ω на время t: α = ω·t.

Таким образом, в рамке - синусоидальная ЭДС e= Em sin ωt.

Если в начальный момент времени t =0 ЭДС не равна нулю, то выражение ЭДС записывается в общем виде:

e= Em sin (ωt + ψе),

где угол ψе учитывает начальное положение рамки.

Через контактные кольца, которые вращаются вместе с рамкой, и через на- ложенные на них неподвижные щетки щ1 и щ2 ЭДС передается на выходные зажимы генератора, образуя на них синусоидальное напряжение u:

u= Um sin (ωt + ψu).

Если замкнуть цепь на приемник (лампа EL), появится синусоидальный ток i = Im sin (ωt + ψi), направление которого в каждом проводнике рамки совпадает

снаправлением индуктированной ЭДС.

2.2.ФОРМЫ ИЗОБРАЖЕНИЯ СИНУСОИДАЛЬНЫХ ЭДС,

НАПРЯЖЕНИЯ И ТОКА

2.2.1. Аналитическая форма

Аналитические выражения синусоидальных функций ЭДС, тока и напря- жения записываются в виде тригонометрических формул:

e = Em sin (ωt + ψе); i = Im sin (ωt + ψi); u = Um sin (ωt + ψu),

где e, i, и - мгновенные значения ЭДС, тока и напряжения, т.е. их значения в произвольный момент времени t;

-Em, Im, Um - амплитуды, т.е. максимальные значения ЭДС, тока и напряжения;

-аргумент синуса (ωt+ ψ) – фаза синусоидальной величины;

-углы ψе, ψi и ψu, определяющие значение е, i и u в момент t= 0, называются

начальной фазой;

-ω - угловая частота. Единица измерения – радиан в секунду [рад/с] или [с–1 ].

e		2.2.2. Графическая форма
e		Временная диаграмма - график измене-
e0		Временная диаграмма - график измене-
Em		ния синусоидальной величины во времени
Em		(рис. 2.3). Полный цикл изменения ЭДС, тока
0	ω	(рис. 2.3). Полный цикл изменения ЭДС, тока
0	ω	t или напряжения называется периодом Т [с].
ψ e		Число периодов в 1 секунду называется
		частотой f = 1/Т. Единица измерения час-
T		тоты - Герц [Гц].
T		Угловая частота ω = 2π f = 2π .
360o, 2π		Угловая частота ω = 2π f = 2π .
		T
Рис. 2.3		Стандартной частоте 50 Гц соответствует

- 22 -

			2. Однофазные электрические цепи
u, i		u		период Т= 0,02 с и угловая частота:
		i		ω = 2π·50= 314 с-1.
				Фаза синусоидальной величины от-
0			ω t	считывается от точки перехода функции
ψ u	− ψ i			через нуль от отрицательных значений к
ψ u	− ψ i			положительным. При ψ > 0 начало сину-
ϕ				соиды сдвинуто влево от начала коорди-
ϕ				нат, а при ψ < 0 – вправо.
				нат, а при ψ < 0 – вправо.
		Рис. 2.4		Разность начальных фаз двух функ-
		Рис. 2.4		ций называется сдвигом фаз. Угол сдви-
				ций называется сдвигом фаз. Угол сдви-
га фаз между напряжением и током обозначается:
			φ= ψu – ψi.
Для рис. 2.4 ψu > ψi и φ= ψu – (- ψi) > 0. Это выражение показывает, что на-
пряжение опережает по фазе ток на угол φ. Возможны также следующие ком-
бинации:
ψu = ψi –		напряжение и ток совпадают по фазе: φ = 0; ψu < ψi – напряжение от-
стает по фазе от тока на угол φ< 0.

2.2.3. Действующие значения

При расчете цепей переменного тока, изменяющиеся во времени ЭДС, токи и напряжения заменяют эквивалентными, неизменными во времени величина- ми - действующими значениями. Обозначаются также как и постоянные вели- чины I, U, E.

Действующее значение переменного тока равняется такому постоянному току, который за время, равное периоду, выделяет в каком-либо сопротивлении такое же количество тепла, что и данный переменный ток.

Для синусоидального тока i = I m sin ωt действующее значение в 2 раз меньше амплитуды:

I = I m .

Действующие значения переменного напряжения и ЭДС:

U = U m ; E = Em .

2 2

Вольтметры и амперметры, предназначенные для работы в цепи синусои- дального тока, градуируются так, чтобы они показывали действующие значе- ния напряжения или тока.

2.2.4. Векторное изображение

Расчет и анализ цепей переменного тока с помощью тригонометрических формул и временных диаграмм весьма громоздок и сложен. Тот же результат может быть получен гораздо быстрее и легче, если представить синусоидаль- ные величины в векторной форме.

Длинна вектора в известном масштабе равна амплитуде синусоидальной величины, например ЭДС Еm. В начальный момент (t = 0) вектор образует с го-

- 23 -

Электротехника и электроника

	у	Em
	e1	Em
	e1			Em
ω	e0	ω	t1	Em
ω	e0	ω	t1
			ψ	е
				х

e
e1
e0
0	ω	t1
ψ е

Рис. 2.5

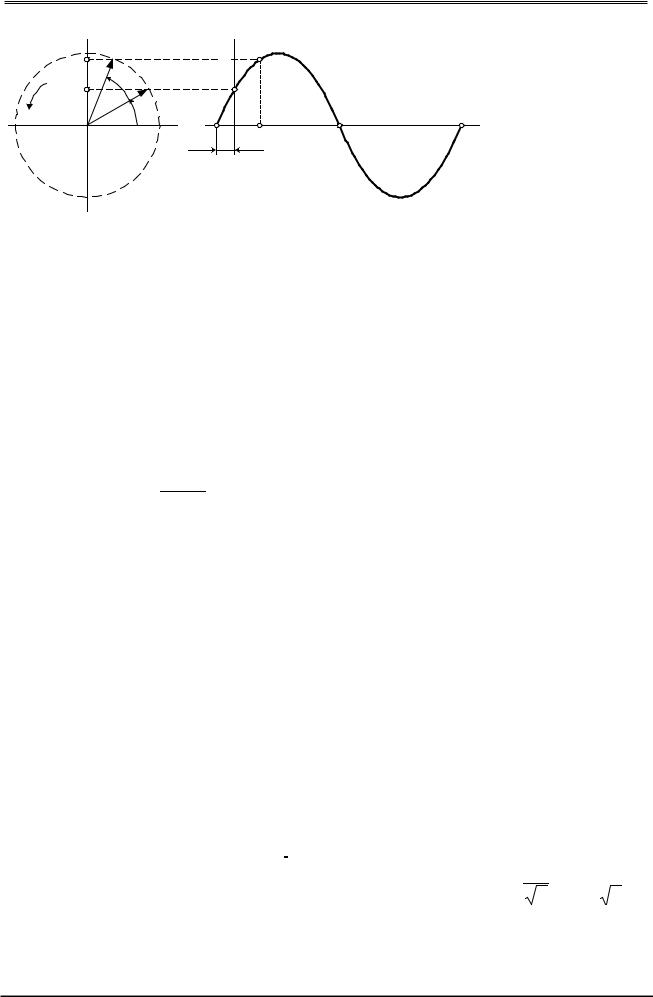
ризонталью угол ψе равный на- чальной фазе

(рис. 2.5). Его

ω t проекция на вер- тикаль в том же масштабе соот- ветствует мгно- венному значе- нию ЭДС:

е0 = Еm sin ψе.

Вектор вращается против направления движения часовой стрелки со скоро- стью равной угловой частоте ω. Тогда в момент времени t1 он образует с гори- зонталью угол ωt1+ ψе и его проекция на вертикаль имеет выражение:

e = Em sin (ωt1 + ψе).

В произвольный момент t:

e = Em sin (ωt + ψе),

то есть получили синусоидальную функцию ЭДС. Конец вектора описывает окружность. Одному обороту вектора (повороту на угол 360º) соответствует один период изменения синусоидальной величины. В технике углы измеряются в радианах. Радиан – угол, дуга которого равна радиусу R, т.е. окружность дли-

ной 2π·R содержит 2π R = 2π радиан. Отсюда соответствие:

угол 360º - 2π, 180º - π, 90º - π/2 и т.д.

Алгебраической сумме мгновенных значений двух синусоидальных вели- чин одинаковой частоты соответствует геометрическая сумма векторов этих величин, которая находится как диагональ построенного на них параллело- грамма.

Совокупность нескольких векторов, которые изображают синусоидальные величины одной частоты, называется векторной диаграммой.

Векторы изображают для момента времени t = 0. Угол ψ считается положи- тельным, если он получается поворотом вектора относительно горизонтали против направления движения часовой стрелки, и отрицательным — в обрат- ном случае. Так как конечной целью расчета являются обычно действующие значения токов или напряжений, то векторные диаграммы строят для дейст- вующих значений величин.

Например, нужно сложить токи: i1= I1m sin ωt, i2= I2m sin (ωt - 90°) . Алгебраической сумме мгновенных значений i= i1+ i2 соответствует сумма

векторов действующих значений: I = I1 + I2.
Длины векторов равны действующим значениям токов: I	1	= I1m	, I	2	=	I2m	.

		2			2

Откладываем векторы I1 и I2 относительно горизонтали с учетом углов:

ψ1= 0° и ψ2 = - 90°.

- 24 -

			2. Однофазные электрические цепи
Чтобы получить вектор I, изображающий суммарный ток i нужно сложить
векторы I1 и I2 по правилу параллелограмма (рис. 2.6).
	I1	ω	Амплитуда суммарного тока Im =					2 I ; начальная

ψ 2 ψ		фаза соответствует углу ψ и имеет отрицательное значе-
		ние.
I			Выражение суммарного тока i = Im sin (ωt - ψ).
I2			Пример 2.1. Напряжение в цепи переменного тока
Рис. 2.6		изменяется по закону u = 280·sin 314t. Определить, что
		покажет вольтметр и частотомер.
			Решение. Общее выражение мгновенного значения
синусоидального напряжения в виде тригонометрической формулы следующее:
u = U m sin ωt .
Вольтметр показывает действующее значение напряжения:
U = U m = 280 = 197 В.
2		2
Так как угловая частота ω= 2π·f, то показания частотомера будут:
f = ω = 314 = 50 Гц.
2π	2π
Пример 2.2. В сети синусоидального тока измерены U = 220 В, f = 50 Гц.
Записать закон изменения напряжения u(t).
Решение. Общее выражение мгновенного значения синусоидального на-
пряжения в виде тригонометрической формулы следующее:
u = U m sin ωt ,						2 U =	2 220 = 311В,
где максимальное значение напряжения Um =
а угловая частота ω = 2π·f = 2π ·50 = 314 c-1.
Получаем закон изменения напряжения: u(t) = 311·sin314·t.
Пример 2.3. Найти ток І3, і3(t), который направлен от узла, если известны
два тока, направленные к узлу:
i1(t) = 3√ 2 sin(314t + 90°) А и i2(t) = 4,24√ 2 sin(314t - 45°) А.
Решение. Согласно первому закону Кирхгоффа для мгновенных значений
I1		тока: Σ i= 0, т.е. i3 = i1+ i2. Для векторов действующих значе-
		ний токов имеем: I3= I1 + I2. Сложение векторов осуществляем
90o	ω	на векторной диаграмме (рис. 2.7). Начальные фазы токов:
		ψ1 = 90° и ψ2 = - 45°. Действующие значения токов:
I3			= I1m = 3	2 = 3 А,		= I 2m = 4,24 2 = 4,24 А.
-45o		I1			I2
			2	2		2	2
I2		Откладываем вектора в масштабе 1А/см. Получили: век-
		тор I3 совпадает с горизонталью, следовательно: ψ3= 0°; длина

Рис. 2.7		вектора I3 равна длине вектора I1					(из равнобедренного тре-
		угольника), то есть I3 = I1 = 3 А.

Максимальное значение тока i3 I3m =					2 I3 = 3		2 А.
Мгновенное значение і3(t) = 3√ 2 sin 314t.
				- 25 -

Электротехника и электроника

2.3. РЕЗИСТИВНЫЙ, ИНДУКТИВНЫЙ И ЕМКОСТНЫЙ ЭЛЕМЕНТЫ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Энергетические процессы, протекающие в цепях переменного тока, прин- ципиально отличаются от процессов в цепях постоянного тока, где при неиз- менных токах и напряжениях электрические и магнитные поля, связанные с це- пью не изменяются. Периодическое изменение напряжений и токов вызывает соответствующее изменение указанных полей. Вследствие изменения магнит- ных полей возникают ЭДС самоиндукции и взаимоиндукции, а при изменении электрических полей протекают зарядные и разрядные токи. Эти процессы ока- зывают непрерывное влияние на работу цепи переменного тока.

Способность объекта преобразовывать электрическую энергию в энергию магнитного поля при нарастании тока, а при снижении – наоборот, характери-

зует индуктивный элемент (рис. 2.8,а).

Энергия магнитного поля WL =

L I 2

, где L – индуктив-

ность. Единица измерения индуктивности – Генри [Гн].

а)

б)

Устройства, предназначенные для накопления энергии в

Рис. 2.8

магнитном поле – катушки индуктивности.

Емкостный элемент (рис. 2.8,б) отображает способ-

ность объекта накапливать электрический заряд и преобразовывать электриче- скую энергию в энергию электрического поля при нарастании напряжения, а при снижении – наоборот.

Энергия электрического поля WС	=	С U m2
		2

, где С – емкость. Единица из-

мерения емкости – Фарада [Ф].

Устройства, предназначенные для накопления энергии в электрическом поле – конденсаторы.

При протекании переменного тока через резистивный элемент электриче- ская энергия преобразуется в другие виды энергии и рассеивается в виде тепла. При этом его сопротивление переменному току больше сопротивления посто- янному току за счет неравномерного распределения тока в сечении проводника и потерь энергии в окружающую среду (см. п.2.6 - явление поверхностного эф- фекта). Это сопротивление называется активным и обозначается r, в отличие от сопротивления постоянному току R.

При расчетах реальные элементы цепи переменного тока заменяют иде- альными, имеющими только один параметр (сопротивление, индуктивность или емкость) и отображающими основные физические процессы в цепи. Такое до- пущение, являясь научной абстракцией, справедливо для большинства практи- ческих расчетов. Например, главное свойство электрических катушек – созда- ние магнитного поля. Поэтому основной их параметр – индуктивность. Вместе с тем при прохождении тока по катушке выделяется тепло, так как провод катушки обладает сопротивлением. В конденсаторе также имеют место потери энергии, которые на низких частотах невелики. Поэтому учитывается только один параметр – емкость.

- 26 -

			2. Однофазные электрические цепи
Основные физические законы, сформулированные для цепей постоянного
тока, справедливы и для цепей переменного тока.
2.3.1. Цепь с резистивным элементом
і	r			u		В цепь с напряжением
		U	m	u			u = Um sin ωt
			m			включен резистор. В схеме за-
			i			включен резистор. В схеме за-
u		Im				мещения (рис. 2.9,а) он пред-
					ω t	ставлен резистивным элемен-
a)			0	π	2π	том с сопротивлением r. По за-
a)						кону Ома мгновенное значение
						кону Ома мгновенное значение
I	U	ω				тока:
I	U	ω				i = u = U m sin ω t = Im sin ω t ,
в)				б)		i = u = U m sin ω t = Im sin ω t ,
в)				б)		r	r
		Рис. 2.9				где Im	= U m - амплитуда тока.
							r
Разделив на 2 обе части равенства, получим выражение закона Ома для дей-
ствующих значений величин:

I = U . r

Ток, также как и напряжение, изменяется синусоидально (временная диа- грамма - рис. 2.9,б). Начальные фазы тока и напряжения одинаковые:

ψu = ψi = 0,

то есть ток и напряжение совпадают по фазе. Графики u и i выходят из начала координат.

Угол сдвига фаз между током и напряжением:

φ= ψu - ψi = 0,

то есть вектор U на векторной диаграмме (рис. 2.9,в) совпадает по направлению с вектором I.

Мгновенная мощность:

p = ui = U

sin 2 ωt = I U

(1 − cos 2ωt ) = I

2 U

(1 − cos 2ωt ) = UI (1 − cos 2ωt )

Из графика мгновенной мощности (рис. 2.10)

видно, что она изменяется с частотой в 2 раза

большей частоты переменного тока. Независимо

от направления тока в цепи мощность всегда по-

ложительна.

Энергия перемещается в одном на-

правлении от источника к приемнику, то есть идет

2π

необратимый процесс преобразования электро-

энергии в другой вид энергии, величина которой

за время t эквивалентна тепловой энергии:

W = I 2r t .

Рис. 2.10

Средняя за период мощность:

- 27 -

Электротехника и электроника

	1	T	1	T
Р =		∫ pdt =		∫[UI − UI cos 2ω t]dt = U I

T		0	T	0

называется активной мощностью. Единица активной мощности – Ватт [Вт]. Активная мощность характеризует среднюю скорость преобразования электри- ческой энергии в тепловую, механическую, химическую и др. виды энергии. Таким образом, резистивный элемент является активным элементом.

Пример 2.4. Построить векторную диаграмму, найти активную мощность Р и потребление энергии резистивным приемником за время работы t = 1 час, если известно U = 200 B, I = 10 A.

Решение. Для резистивного приемника: P = U·I = 200·10= 2000 Вт= 2 кВт.

Потребляемая энергия W = I 2r t = P t = 2 1 = 2 кВт·час.	I	U
Угол сдвига фаз между напряжением и током φ= 0, то есть
Угол сдвига фаз между напряжением и током φ= 0, то есть
на векторной диаграмме (рис. 2.11) вектор U совпадает по на-	Рис. 2.11
правлению с вектором I.	Рис. 2.11
правлению с вектором I.

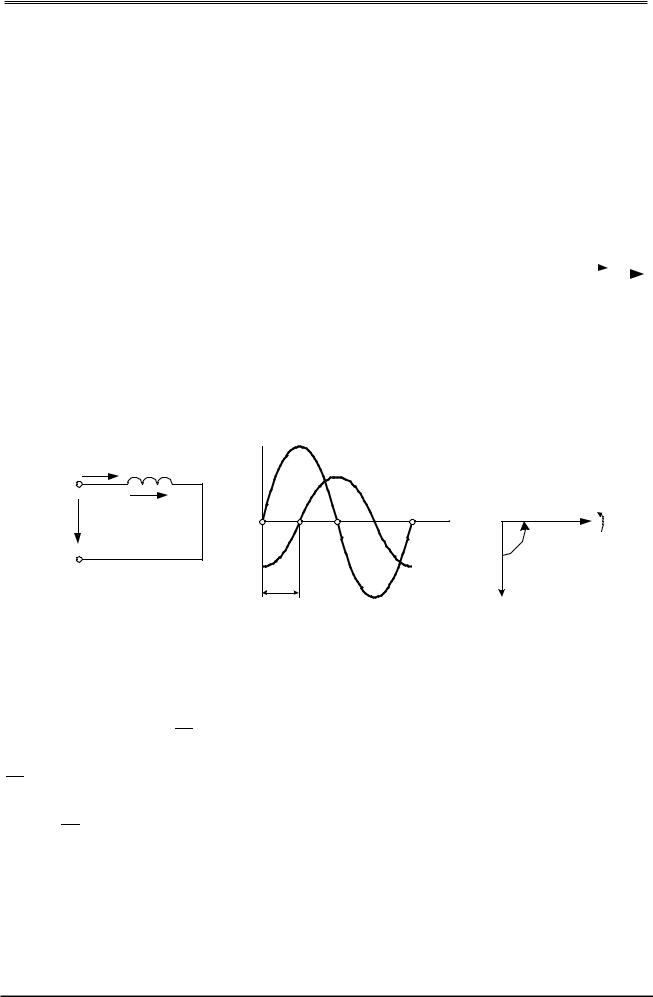
2.3.2. Цепь с индуктивным элементом

В цепь с напряжением u = Um sin ωt включена катушка индуктивности. В схеме замещения (рис. 2.12,а) она представлена индуктивным элементом с индуктивностью L.

i	L
u	eL
u

u, i	u
		i
0		ω	t	U	ω
0	π	2π
	π	2π	ϕ	= 900
			ϕ	= 900
ψ	=−900	б)	I	в)
ψ	=−900	б)		в)
	i
	Рис. 2.12

Под действием приложенного напряжения по цепи проходит переменный ток, который создает переменный магнитный поток, индуктирующий ЭДС са-

моиндукции: eL = −L di . Знак минус указывает, что при возрастании тока (когда dt

di > 0) ЭДС самоиндукции направлена навстречу току, а при уменьшении тока dt

(когда di <0) - совпадает по направлению с током, то есть в соответствии с за- dt

коном Ленца ЭДС eL противодействует изменению тока.

Согласно второму закона Кирхгоффа: u = - eL или u = L							di	. Тогда:

							dt
	1	T	U m		U m
i =		∫U m sin(ω t)dt =		cosω t =		sin(ω t − 90 ) = Im sin(ω t − 90 ) ,
			ω L
	L 0				ω L

- 28 -

2. Однофазные электрические цепи

где Im =

U m

- амплитуда тока. Разделив на

2 обе части равенства, получим

ω L

выражение закона Ома для действующих значений величин:

I = U ,

Х L

где ХL= ωL= 2 π f L - индуктивное сопротивление [Ом].

На временной диаграмме (рис. 2.12,б) ток изменяется синусоидально.

Начальная фаза тока

ψi

= − π = −90o .

Угол сдвига фаз

ϕ = ψu − ψi = π ,

то есть напряжение опережает ток на 90º. Векторная диаграмма напряжения и

тока представлена на рис. 2.12,в. Угол φ отсчитывают от вектора I к вектору U.

Мгновенная мощность:

p = ui = −U

sin ω t cosω t = −I U

sin 2ω t = −UI sin 2ω t

m m

изменяется синусоидально с частотой, вдвое большей частоты переменного то-

ка (рис. 2.13). Мгновенная мощность положи-

тельная пока ток в цепи возрастает - происходит

накопление энергии в магнитном поле катушки.

Когда ток убывает, мощность отрицательная —

ω t

энергия возвращается источнику.

Средняя за период, т.е. активная мощность:

2π

Р = 0 .

В цепи происходит периодический обмен

энергией между источником и приемником без

преобразования ее в другие виды. Эта энергия

характеризуется

реактивной

индуктивной

Рис. 2.13

мощностью:

QL= U·I= I2·XL.

Единица реактивной мощности - вольт-ампер реактивный [вар].

Таким образом, индуктивный элемент является реактивным элементом.

Пример 2.5. Построить векторную диаграмму, найти активную мощность

Р и потребление энергии индуктивным приемником ХL за время работы t = 1час,

если известно U = 200 B, I = 10 A. Определить реактивную индуктивную мощ-

ность.

Решение. Для индуктивного приемника: P = 0 Вт.

Потребляемая энергия W = I 2r t = P t = 0 1 = 0 Вт·час.

Угол сдвига фаз между напряжением и током ϕ = π , то есть

Рис. 2.14

на векторной диаграмме (рис. 2.14) вектор напряжения U опе-

режает вектор тока I на 90º.

Реактивная индуктивная мощность QL = U·I = 200·10 = 2000 вар= 2 квар.

- 29 -

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.05.2019166.4 Кб3jittya_cinnist.doc
#
03.03.2016804.45 Кб14k481.pdf
#
03.03.201676.43 Кб4khuy.docx
#
03.03.2016387.96 Кб14Komponenty_sredy_Grasshopper.pdf
#
03.03.20162.51 Mб11Komunalne_pravo_metodichka.rtf
#
03.03.20166.68 Mб34KonspektElektrotekhnika_i_elektronika.pdf
#
22.11.20194.08 Mб2Konspekt_lektsiy.doc
#
03.03.20163.71 Mб37konspekt_lektsy_mikro.doc
#
03.03.2016871.94 Кб10Konspekt_po_PE_1chast.doc
#
03.03.20166.04 Mб25kpi Moy Kurcach.docx
#
03.03.20164.99 Mб31KR-2005.doc