Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

KonspektElektrotekhnika_i_elektronika

.pdf

Скачиваний:

Добавлен:

03.03.2016

Размер:

6.68 Mб

Скачать

☆

<<< < Предыдущая 12 / 122 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

Электротехника и электроника

U1= I·R1; U2 =I·R2; … Un = I·Rn.

По второму закону Кирхгоффа для рис. 1.6,а:

	U
I	R1
U	U1

=U1 + U 2

+ ... + U n	k =n
+ ... + U n	= ∑U k .
	k =1
R		I	R
n		I	экв



Un	U
Un	U

а)	б)
	Рис. 1.6

Напряжение и ток в цепи с эквивалентным сопротивлением остаются теми же: U=I·Rэкв, тогда:

IRэкв = I (R1 + R2 + ... + Rn )= I k∑=n Rk .

k =1

Rэкв = R1 + R2 + ... + Rn = ∑Rk ,

k =1

то есть эквивалентное сопротивление последовательно соединенных элементов равно сумме их сопротивлений.

Мощность всей цепи равна сумме мощностей отдельных приемников:

Р = I2·Rэкв = I2·R1 + I2·R2 +…+ I2·Rn = Р1+ P2 +...+Рn.

Таким образом, напряжение и мощность распределяются между последова- тельно соединенными приемниками прямо пропорционально их сопротивлени- ям.

Недостаток последовательного соединения: при выходе из строя одного приемника цепь не работает.

Применяется, когда приемники рассчитаны на напряжение меньшее, чем напряжение источника.

I	R1	R2
U	UR1	UR2

Рис. 1.7

Пример 1.3. В цепи с последовательным соедине- нием элементов (рис. 1.7) с сопротивлениями R1 и R2 известны: UR1 = 70 В, R1 = 7 Ом, R2 = 3 Ом. Определить ток в цепи I, напряжение на выводах элемента с сопро- тивлением R2 и общее напряжение.

Решение. По закону Ома находим ток в цепи:

I = U R1 = 70 = 10 А.

R1 7

Напряжение на выводах элемента с сопротивлением R2:

U R 2 = I R2 = 10 3 = 30 В.

Общее напряжение (напряжение на зажимах цепи):

U = I (R1 + R2 ) = 10 (3 + 7) = 30 + 70 = 100 В.

- 10 -

1.Цепи постоянного тока

1.5. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ПРИЕМНИКОВ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ

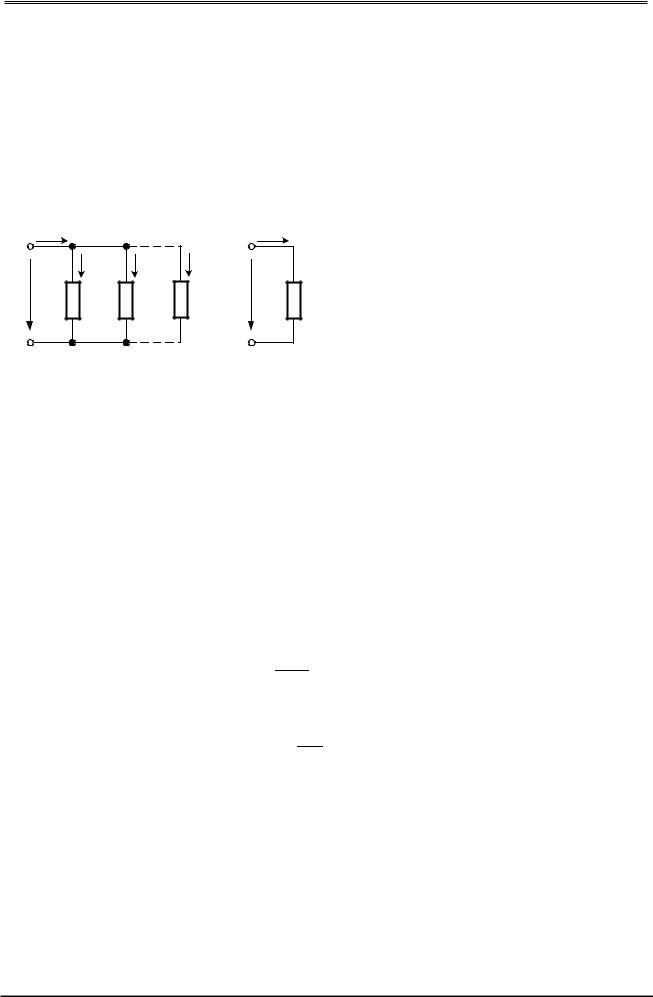
На рис. 1.8,а изображена схема с параллельным соединением элементов; на рис. 1.8,б – эквивалентная схема замещения.

Параллельно включенные ветви с сопротивлениями R1, R2 и Rn находятся под одним и тем же напряжением U. По закону Ома токи в ветвях:

= U G ;. I

= U G

... I

= U G

I I

	I1	I2	In
U	R	R	R	U	R
	1	2	n		экв

а)

б)

Рис. 1.8

Тогда:

Сумма этих токов, согласно первому закону Кирхгофа, равна то- ку I в неразветвленной части цепи:

I = I1 + I 2 + ...I n .

Таким же будет и ток на участке с сопротивлением Rэкв (рис. 1.8.б) эквивалентным данным n сопротив-

лениям: I =	U	= U Gэкв .
	Rэкв

	U	=	U	+	U	+ ... +	U	.
		=		+		+ ... +		.
	Rэкв		R1		R2		Rn
Получаем:
1		=	1	+	1	+ ... +	1	,
		=		+		+ ... +		,
	Rэкв		R1		R2		Rn

то есть при параллельном соединении, складывая величины обратные сопро- тивлениям (проводимости ветвей), получают обратную величину эквивалент- ного сопротивления цепи (эквивалентную проводимость):

Gэкв= G1 + G2 +…+ Gn.

Имея Gэкв, определяют Rэкв = 1 .

Gэкв

Мощности параллельно соединенных ветвей определяют по формуле:

Pn = U 2 = U 2Gn . Rn

Мощность всей цепи равна сумме мощностей отдельных приемников:

Р= Р1+ P2 +...+Рn.

Из соотношений видно, что ток и мощность распределяются между парал- лельными ветвями прямо пропорционально их проводимостям.

Преимущество: независимое включение приемников.

Пример 1.4. В цепи с параллельным соединением элементов (рис. 1.9) с сопротивлениями R1 и R2 известны U = 100 В, I1 = 1 А, R2=100 Ом. Определить мощности элементов Р1 и Р2.

- 11 -

Электротехника и электроника

	I
	I1	I2
U	R1	R2

Решение. Параллельно соединенные ветви находятся под одним напряжением. Тогда для ветви с сопротивлени- ем R1:

Р1 = U I1 = 100 1 = 100 Вт.

Для ветви с сопротивлением R2:

	Р =	U 2	=	1002	= 100 Вт.
Рис. 1.9

	2	R2	100

1.6. РАСЧЕТ РАЗВЕТВЛЕННОЙ ЦЕПИ С ОДНИМ ИСТОЧНИКОМ ЭДС

Разветвленные цепи с одним источником ЭДС рассчитывают методом эк- вивалентных преобразований, который заключается в замене отдельных участ- ков цепи с параллельным или последовательным соединением элементов экви- валентными сопротивлениями.

Для примера рассмотрим цепь, которая состоит из генератора и смешанно- го соединения (последовательного и параллельного) участков с сопротивле- ниями R1, R2, R3 и R4 (рис. 1.10). Параллельно соединенные ветви включены ме- жду узлами а и b цепи.

С целью упрощения схемы находим эквивалентное сопротивление для па- раллельных ветвей.

Проводимости параллельных ветвей:

1 ; G

= 1 ;

= 1 .

Uаb

Тогда эквивалентная проводимость:

234

= G

+ G + G

Эквивалентное сопротивление:

R234

Рис. 1.10

G234

После замены ветвей с сопротивлениями R2, R3 и R4 эквивалентным сопро- тивлением R234, получаем цепь с последовательным соединением двух элемен- тов с сопротивлениями R1 и R234 (рис. 1.11), которые заменяем одним эквива- лентным сопротивлением:

R1234= R1 + R234.

Находим ток в неразветвленной части цепи:

Uаb

R1234

R234

Определяем падение напряжения на выводах а-b

участка цепи с эквивалентным сопротивлением R234:

Uab= R234·I1.

Находим токи в параллельных ветвях:

Рис. 1.11

U ab

; I

U ab

;

U ab

- 12 -

1.Цепи постоянного тока

Пример 1.5. Найти эквивалентное сопротивление цепи

(рис. 1.12), если R1 = R2

= 6 Ом, R3 = R4 = R5 = 3 Ом.

Решение.

Определяем

эквивалентную проводимость

ветвей с R1 и R2:

G12 =

-1

R12

Ом

Эквивалентное сопротивление: R12	=	1	= 3 Ом.	Рис. 1.12

		G12

Определяем эквивалентную проводимость ветвей с сопротивлениями R3,

R4, R5:

G345 =

= 1Ом-1.

R12 R345

R345

Эквивалентное сопротивление: R345 =

= 1Ом.

G345

Рис. 1.13

Врезультате преобразований получили схему (рис. 1.13)

споследовательным соединением элементов с сопротивлениями R12 и R345. То- гда эквивалентное сопротивление цепи: Rэкв = R12 + R345 = 3 + 1 = 4 Ом.

Пример 1.6. Для схемы рис. 1.14 найти эквивалентное сопротивление цепи,
если R1= R2= R3= R4= R5= 2 Ом.	R2	R3
Решение. Определяем эквивалентные сопротивления
	R1
ветвей с последовательным соединением резисторов R2 и		R
	R
R3, R4 и R5:	4	5

R23 = R2 + R3 = 2 + 2 = 4 Ом;	Рис. 1.14
R45 = R4 + R5 = 2 + 2 = 4 Ом.

Находим эквивалентную проводимость ветвей, соединенных параллельно

(ветви с резисторами R23 и R45): G2345 =

Ом-1.

R2345

R45

R23

Эквивалентное сопротивление: R

= 2

Ом.

R1 R2345

2345

G2345

Получаем схему (рис. 1.15) с последовательным соедине-

нием элементов с сопротивлениями R1 и R2345. Тогда эквива-

лентное сопротивление цепи: RЭКВ = R1 + R2345 = 2 + 2 = 4 Ом.

Рис. 1.15

1.7. РАБОТА ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПОСТОЯННОГО ТОКА ПРИ ПЕРЕДАЧЕ ЭНЕРГИИ ОТ ИСТОЧНИКА К ПРИЕМНИКУ

1.7.1. Потери напряжения и мощности

Цепь (рис. 1.16) содержит генератор с ЭДС Е и внутренним сопротивлени- ем R0, линию электропередачи (ЛЭП) с сопротивлением каждого провода Rлэп и нагрузку. Сопротивление нагрузки Rн может меняться.

По закону Ома ток в цепи:

- 13 -

Электротехника и электроника

Rлэп

I =

+ 2Rлэп + Rн

ЭДС источника:

E = R0 I + U1= R0 I + 2Rлэп I + Rн I.

Это уравнение называется уравнением элек-

Rлэп

трического состояния цепи.

Напряжение на зажимах источника энергии

Рис. 1.16

U1, то есть в начале ЛЭП, меньше ЭДС на вели-

чину внутренней потери напряжения ∆U0 = I·R0 (рис. 1.17):

U1 = E - I R0 = E - ∆U0.

Напряжение в конце ЛЭП U2 меньше напряжения на зажимах

источника U1 на величину потери напряжения в линии (рис. 1.18)

Rлэп

∆Uлэп = 2I Rлэп.

лэп

U2 = U1-2I Rлэп = U1 - ∆U .

Это

напряжение поступает

на нагрузку

Рис. 1.17

(рис. 1.16) U2 = R I.

Умножив уравнение электрического со-

стояния на величину тока I, получим уравнение распределе-

ния мощности в цепи:

лэп

E·I = I2 R0 + 2I2 Rлэп + I2 Rн,

Рис. 1.18

где Pг = E·I - электрическая мощность развиваемая в источ-

нике электрической энергии. Часть ее ∆P0 = I2

R0 теряется

(превращается в тепло) внутри самого источника, а остальная мощность отда-

ется во внешнюю цепь:

P1= U1·I = Pг- I2 R0.

Часть мощности превращается в тепло при передаче (в проводах ЛЭП). Ве-

личина потери мощности в линии:

∆Pлэп= 2I2 Rлэп = ∆Uлэп I.

Таким образом, потери мощности: ∆P = I2 R0 + 2I2 Rлэп, как и потери напря- жения, связаны с наличием сопротивлений Rлэп и R0.

Мощность, отдаваемая через ЛЭП приемнику:

P2 = U2 I= Pг - ∆P.

Эта мощность потребляется нагрузкой:

					P2 = I2 Rн.
Пример 1.7. К ЛЭП с Rлэп = 0,2 Ом и U1 = 100 В (напряжение в начале ли-
	I		R		нии) параллельно подключается группа ламп, коли-
			R		чество которых может изменяться от 0 до ∞ . Опреде-
			лэп

					лить напряжение на лампах, если ток в ЛЭП 10 А.
			U2	Rн


U1					Для схемы замещения цепи (рис. 1.19), по второ-
					му закону Кирхгоффа:
					му закону Кирхгоффа:
					U1 = ∆ U лэп + U 2 = I Rлэп + U 2 , откуда:
		Рис. 1.19			U1 = ∆ U лэп + U 2 = I Rлэп + U 2 , откуда:
		Рис. 1.19			U 2 = U1 − I Rлэп =100 −10 0,2 = 98 В.
					U 2 = U1 − I Rлэп =100 −10 0,2 = 98 В.

- 14 -

1.Цепи постоянного тока

1.7.2. Коэффициент полезного действия ЛЭП.

Пути повышения мощности, передаваемой по ЛЭП

Коэффициент полезного действия (КПД) ЛЭП - отношение отдаваемой ли- нией приемнику мощности Р2 = U2·I к получаемой ею от источника мощности

Р1= U1·I.

ηлэп

Р1 − ∆ Рлэп

=1 −

∆ Рлэп

=1 −

∆ U лэп I

=1 −

∆ U лэп

Из формулы мощности P = U·I видно, что одна и та же мощность может быть получена при более высоком напряжении и меньшем токе или при боль-

шем токе и низком напряжении. Для того чтобы уменьшить потери напряжения ∆Uлэп = 2I Rлэп и мощности ∆Pлэп = 2I2 Rлэп = ∆Uлэп I в проводах при передаче

электрической энергии и повысить КПД ЛЭП, уменьшают ток в проводах, во столько же раз увеличивая напряжение.

Например, при напряжении U´= 2U и той же мощности P´= P ток будет ра- вен I´= I / 2. При прежнем сопротивлении проводов Rлэп потеря напряжения в ЛЭП составит:

∆U´лэп = I´ 2Rлэп = 2Rлэп I / 2=∆Uлэп / 2.

Потеря мощности будет теперь:

∆ U лэп

∆ Pлэп

∆ Р

лэп

= P

− P

= ∆ U

лэп

то есть уменьшится в четыре раза.

1.7.3.Режимы холостого хода и короткого замыкания.

Защита электрической цепи от токов короткого замыкания

В зависимости от сопротивления нагрузки различают:

а) сопротивление нагрузки Rн → ∞ – режим холостого хода.

При разомкнутой цепи ток I = 0 и напряжения равны ЭДС источника:

U1= U2 = E.

Мощность нагрузки P2= I2 R2= 0. В этом режиме потери напряжения и мощности отсутствуют:

∆U = ∆U0 + ∆Uлэп = I R0 + 2I Rлэп = 0, ∆P = ∆U I = 0.

Тогда КПД всей цепи:

η =

Р − ∆ Р

U 2 I

U 2

Е − ∆ U

=1 (η = 100%).

Е I Е

б) Rн = 0 – режим короткого замыкания.

Тогда U2 = I Rн = 0.

При этом ток

I = Iкз =

= max

+ 2Rлэп + Rн

+ 2Rлэп

и может достигать очень больших значений, так как R0 и Rлэп во много раз меньше сопротивления приемников Rн.

Мощность, развиваемая генератором Pг = E Iкз = max. Мощность, отдаваемая через ЛЭП нагрузке P2 = U2·I = 0.

- 15 -

Электротехника и электроника

КПД η = P2 = 0 . Pг

Вся мощность теряется во внутреннем сопротивлении генератора и прово-

дах ЛЭП ∆P = I2 R0 + 2I2 Rлэп = Pг – P2 = Pг.

Режим короткого замыкания – аварийный. Токи короткого замыкания пере- гревают провода и могут повредить линию передачи и электрическое оборудо- вание.

Для защиты электрических цепей от токов короткого замыкания использу- ют защитные устройства, которые быстро отключают цепь.

Пример 1.8. Определить параметры схемы замещения реального источника ЭДС Е, если известно напряжение в режиме холостого хода Uхх = 40В и ток ко- роткого замыкания Iкз = 4 А.

Решение. Схема замещения реального источника ЭДС содержит идеаль- ный источник ЭДС и идеальный резистивный элемент с сопротивлением R0.

ЭДС источника определим исходя из режима

холостого хода (рис. 1.20,а):

E = Uxx= 40 B.

кз

При коротком замыкании (рис. 1.20,б):

хх

Iкз

а)

б)

Откуда внутреннее сопротивление источника:

Рис. 1.20

= 10 Ом.

Iкз

1.7.4. Согласованный и номинальный режимы работы

Соотношение Rн= R0 + 2Rлэп определяет условие согласованного режима.

В этом режиме мощность нагрузки максимальна:

Р2max = U 2 I =

E 2 Rн

E 2

(R + 2R

лэп

+ R )2

4(R + 2R

лэп

)

Ток в цепи I =

Iкз

+ 2Rлэп )

R0 + 2Rлэп + Rн

2(R0

Напряжение на выводах нагрузки

= I R =

2(R0 + 2Rлэп ) н

U 2 I

КПД: η =

U 2

= 50 %,

Е I Е

то есть при передаче энергии в согласованном режиме теряется половина мощ- ности.

Для эффективной передачи энергии по ЛЭП потери нормируются и не должны превышать 10%. Поэтому для электрических сетей в качестве рабочего выбирается режим с η=90…95% , который называется номинальным.

- 16 -

1.Цепи постоянного тока

, Р ,

Номинальный режим рабо-

ты всех источников и приемни-

U2, η

ков

электроэнергии

характери-

зуется

номинальными

значе-

P =EI

ниями напряжения Uном и тока

Iном,

которые устанавливает раз-

работчик и изготовитель.

0,5

Работу электрической цепи

при

изменяющейся

нагрузке

U =E/2

можно оценить с помощью за-

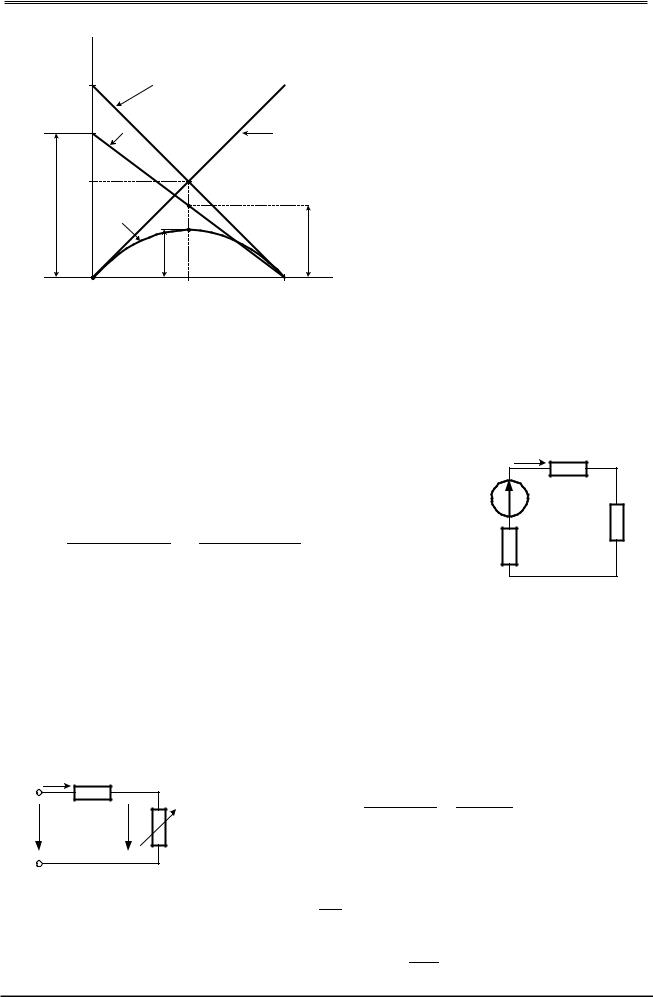
висимостей U(I), Рг(I), Р2(I), η(I),

P2max

которые

представлены

на рис.

1.21.

Пример 1.9. ЭДС источни-

кз

Рис. 1.21

ка Е = 100 В, внутреннее сопро-

тивление R0 = 0,1 Ом, сопротив-

ление ЛЭП Rлэп = 10 Ом. Для согласованного режима определить сопротивление

нагрузки и потребляемую приемником мощность.

Решение. Схема замещения цепи представлена на рис. 1.22.

Сопротивление нагрузки при согласованном режи-

ме:

лэп

Rн = R0 + Rлэп = 0,1 + 10 = 10,1Ом.

Ток в цепи

I =

100

= 4,95 А.

+ Rлэп

+ R н

+ 10 + 10,1

0,1

Мощность, потребляемая приемником:

Рис. 1.22

Р = I 2 R =

4,952 10,1 = 247,5 Вт.

Пример 1.10. К ЛЭП с Rлэп = 50 Ом подключается группа ламп, соединен-

ных параллельно. Количество ламп может изменяться от 0 до ∞ . Напряжение в

начале линии U1 = 220 В. Требуется нарисовать схему замещения; определить

возможную максимальную мощность, потребляемую лампами и КПД.

Решение. Схема замещения цепи представлена на рис. 1.23. Максимальная

мощность будет при согласованном режиме работы. В этом режиме:

лэп

Rлэп = Rн = 50 Ом.

220

Ток в цепи I =

= 2,2

А.

Rлэп + Rн

50 + 50

Потребляемая лампами мощность:

Рн = Рмакс = I 2 Rн = 2,22 50 = 242 Вт.

Рис. 1.23

КПД η = Рн , где мощность, получаемая ЛЭП от

Р1

источника

Р = U

I = 220 2,2 = 248 Вт. Тогда η = 242

= 0,98 или 98%.

248

- 17 -

Электротехника и электроника

1.7.5.Работа источника ЭДС генератором и приемником электрической энергии

В схеме замещения реального источника электрической энергии присутст- вуют два идеальных элемента, которые учитывают два процесса: 1 - способ- ность создавать разность потенциалов на выводах и порождать ток в замкнутой электрической цепи (идеальный источник ЭДС); 2 - внутреннее тепловыделе- ние при прохождении тока через источник (идеальный резистивный элемент с сопротивлением R0).

При работе источника генератором ток совпадает по направлению с ЭДС (рис. 1.24,а). Напряжение на выводах реального источника:

	U			U		U = E – R0I,
	U			U		то есть вследствие потери напряже-
						то есть вследствие потери напряже-
I	E	R0	I	E	R0	ния на внутреннем сопротивлении
						R0I, напряжение на зажимах источни-
	а)			б)		ка электрической энергии меньше его
	а)			б)		ЭДС U < E. Генератор отдает энергию
		Рис. 1.24				во внешнюю цепь (E·I > 0).
При работе источника приемником в нем происходит превращение элек-
трической энергии в другие виды энергии: химическую - в заряжающемся ак-
кумуляторе, механическую - в электродвигателе и т.п. Ток и ЭДС имеют проти-
воположные направления (рис. 1.24,б). Напряжение на выводах:

			U = E + R0I,
то есть напряжение на зажимах приемника больше его ЭДС U > E на величину
потери напряжения R0I.
Приемник получает мощность: P = EI + R0I2, часть которой ∆Р0 = R0I2 соот-
ветствует тепловым потерям в приемнике, а часть E·I представляет собой мощ-
ность, преобразуемую в химическую или механическую формы (E·I < 0).
Пример 1.11. К сети постоянного тока с напряжением U = 6 В (рис. 1.25)
подключен аккумулятор с ЭДС E = 5 В и внутренним сопро-					+
тивлением R0 = 1 Ом. В каком режиме работает батарея? Оп-
					-
ределить ток батареи.					Q
Решение. Схема замещения цепи представлена на рис.
					+ G
1.26. Задаем направление тока в цепи и составляем уравнение
по второму закону Кирхгоффа: Е = U − I R0 .
+		-	Откуда I = U − E = 6 − 5 =1А.		Рис. 1.25

E	R0	I	R0	1
			Положительное значение тока означает, что произ-

Рис. 1.26			вольно выбранное направление тока совпадает с действи-
			тельным (в противном случае получим отрицательное зна-
			чение)
Ток направлен от зажима «+» к зажиму «-», то есть противоположно на-
правлению ЭДС, следовательно, аккумулятор работает в режиме приёмника.

- 18 -

1.Цепи постоянного тока

Пример 1.12. Найти токи во всех элементах цепи представленной на рис. 1.27,а. Известны: Е = 50 В, R1 = 10Ом, R2 = 4 Ом, R3 = R4 = 2 Ом.

Решение. Задачу решаем методом эквивалентных преобразований. Эквивалентное сопротивление ветви с последовательным соединением

элементов R3 и R4:

R34 = R3 + R4 = 2 + 2 = 4 Ом.

Параллельно соединенные ветви с сопротивлениями R2 и R34 (рис. 1.27,б) заменим одним сопротивлением R234. Эквивалентная проводимость ветвей:

G234 =	1	= 1 +	1	= 1 + 1 = 2 = 1 Ом-1.
	R234	R2	R34	4 4 4	2
Тогда эквивалентное сопротивление R							=	1	= 2 Ом.
					234			G234
								G234
I1	R1	a		I1	R1	a			I1	R1 a
		I2	I3=I4					I2	I3=I4
E				E	Uаb				E	Uаb
E	Uаb	R2	R3		Uаb			R2	R34	Uаb	R234
	Uаb	R2	R3					R2	R34		R234
			R4			b				b
		b
	а)				б)					в)
					Рис. 1.27

Ток в неразветвленной части цепи с последовательным соединением R1 и

R234 (рис. 1.27,в):

I1	=		E	=	50		= 4,16 А.
		R1	+ R234			2
				10 +

Напряжение на зажимах параллельных ветвей (между узлами а и b):

U аb = I1 R234 = 4,16 2 = 8,32 B.

Токи в параллельных ветвях:

U аb

8,32

= 2,08A; I

3 = I

U аb

8,32

= 2,08 A.

R34

Для проверки можно составить баланс мощностей: ∑EI = ∑RI²- алгебраи- ческая сумма мощностей источников электрической энергии должна быть рав- на арифметической сумме мощностей, расходуемых всеми потребителями. До- пустимая погрешность – 5%.

Для схемы на рис. 1.27 имеем: E I1 = R1 I12 + R2 I 22 + R3 I32 + R4 I42 . 50 4,16 ≈ 10 4,162 + 4 2,082 + 2 2,082 + 2 2,082 .

Окончательно: 208 Вт ≈ 207,66 Вт.

Погрешность 208 − 207,66 100 = 0,16 % меньше допустимой. 208

- 19 -

<<< < Предыдущая 12 / 122 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.05.2019166.4 Кб3jittya_cinnist.doc
#
03.03.2016804.45 Кб15k481.pdf
#
03.03.201676.43 Кб5khuy.docx
#
03.03.2016387.96 Кб14Komponenty_sredy_Grasshopper.pdf
#
03.03.20162.51 Mб11Komunalne_pravo_metodichka.rtf
#
03.03.20166.68 Mб34KonspektElektrotekhnika_i_elektronika.pdf
#
22.11.20194.08 Mб2Konspekt_lektsiy.doc
#
03.03.20163.71 Mб38konspekt_lektsy_mikro.doc
#
03.03.2016871.94 Кб10Konspekt_po_PE_1chast.doc
#
03.03.20166.04 Mб25kpi Moy Kurcach.docx
#
03.03.20164.99 Mб31KR-2005.doc