V. Соотношения в прямоугольном треугольнике.
-
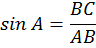
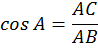
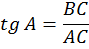
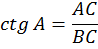
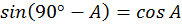
A
CM
BM
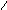
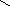
D
M
Если
B
= 300,
то 
AB2 = AC2 + DC2 (Теорема Пифагора)
Если CD - высота, а CM - медиана, то:
;
;
.
AM = MB = CM = R
V. Таблица значений тригонометрических функция для острых углов.
-
300
450
600
sin
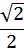
cos
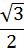
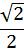
tg
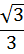
1
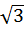
ctg
1
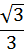
V. Свойства равнобедренного треугольника.
Углы при основании равнобедренного треугольника равны.
Медиана равнобедренного треугольника, проведенная к основанию, является также биссектрисой и высотой.
V. Свойство касательной.
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Х. Вписанные и описанные окружности.
В любой треугольник можно вписать окружность и притом только одну.
Около любого треугольника можно описать окружность и притом только одну.
В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 1800.