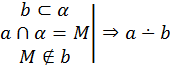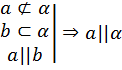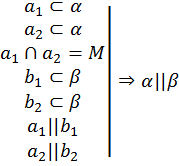§ 2. Взаимное расположение прямых и плоскостей в пространстве.

 . Основные аксиомы стереометрии и следствия из них.

Как и планиметрия, стереометрия изучается в том же структурном плане: формулируются аксиомы (утверждения, принимаемые без доказательства ввиду их очевидности), теоремы (утверждения, которые доказываются с опорой на аксиомы, определения и ранее изученные теоремы) и определения.

Сформулируем три аксиомы, выражающие основные свойства плоскостей в пространстве.

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома 2. Если две точки прямой принадлежат плоскости, то и вся прямая лежит в этой плоскости.

Аксиома 3. Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (т.е. плоскости имеют общую прямую, на которой лежат все общие точки этих плоскостей).

Следствием этих аксиом являются следующие теоремы (доказательства этих теорем и всех последующих опускаем):

Теорема 1. Через прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.

Теорема 2. Через две пересекающиеся прямые можно провести плоскость, и притом только одну.

Теорема 3. Через две параллельные прямые можно провести единственную плоскость.

. Взаимное расположение прямых.

Возможны три случая: две прямые параллельны, пересекаются или скрещиваются.

Определение. Две прямые называются пересекающимися, если они имеют одну общую точку. Обозначение: a ∩ b = M

α a b M

Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. Обозначение: a || b

a α b

Определение. Две прямые, не лежащие в одной плоскости, называются скрещивающимися. Обозначение: a ∸ b

a b M α

Теорема 4 (признак скрещивающихся прямых): Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.

Пример: Две прямые, содержащие ребра AA1 и CD куба ABCDA1B1C1D1 являются скрещивающимися.

С1 В1 D1 А1 В С D А

. Взаимное расположение прямой и плоскости.

Возможны три случая: прямая лежит в плоскости; прямая пересекает плоскость; прямая и плоскость параллельны.

Определение. Прямая, все точки которой принадлежат плоскости, называется прямой, лежащей в плоскости. Обозначение: a  α	a α
Определение. Прямая и плоскость называются пересекающимися, если у них есть одна общая точка. Обозначение: a ∩ β = M	a β M

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Обозначение: a ||  a ∩ β = 

Теорема 5 (признак параллельности прямой и плоскости): Если прямая, не лежащая в плоскости, параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна данной плоскости.

a b α

V. Взаимное расположение плоскостей.

Возможны два случая: две плоскости пересекаются или параллельны.

Определение. Две плоскости называются параллельными, если они не имеют общих точек

Теорема 6 (признак параллельности плоскостей): Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны.		a1 a2 α M b1 b2 β
Определение. Две плоскости называются пересекающимися, если они имеют общую прямую. В этом случае они не имеют других общих точек вне этой прямой. α ∩ β = a		β α a
	Вопросы и задачи

601. Дан куб ABCDA₁B₁C₁D₁. Точка М – середина ребра B₁C₁, N – середина C₁D₁, K – середина DC, О – точка пересечения диагоналей основания ABCD. Укажите взаимное расположение между следующими прямыми:

а) АA₁ и CС₁; б) A₁C₁ и B₁D₁; в) A₁C₁ и C₁D₁;

г) A₁М и CC₁; д) A₁D и DC₁; е) A₁C₁ и BD;

ё) A₁C и АС; ж) A₁B и D₁С; з) A₁C и ВB₁;

и) A₁D и АВ ; й) A₁М и ВС; к) A₁М и ВК ;

л) C₁К и B₁N; м) C₁О и AB₁; н) A₁О и B₁D.

601. Дан тетраэдр ABCD. Точка К – середина ребра AD, L – середина DB, М – середина АС, N – середина ВС. Определите взаимное расположение прямых и плоскостей.

а) DB и AMN; б) MN и ABC; в) КС и DMN;

г) MN и ABD; д) KL и DMN; е) LN и KML;

ё) CL и ADN; ж) LN и DMK.

601. Дан куб ABCDA₁B₁C₁D₁. Точка К – середина ребра AD, L – середина СC₁, М – середина A₁B₁, N – середина B₁C₁, Т – середина DC, О – точка пересечения диагоналей четырёхугольника ABCD. Укажите взаимное расположение плоскостей:

а) A₁B₁C₁ и ADC; б) MTK и BB₁D; в) MNK и MNT;

г) D₁KT и BMN; д) MNK и TLN; е) B₁КТ и DMN;

ё) A₁DC₁ и АB₁C; ж) A₁C₁С и MKT.

641. Отметьте верные утверждения

а) через точку, не принадлежащую данной прямой, можно провести только одну прямую, параллельную этой прямой.

б) через точку, не принадлежащую данной прямой, можно провести только одну прямую, перпендикулярную этой прямой.

в) прямые, перпендикулярные одной и той же прямой, параллельны.

г) прямая, пересекающая одну из двух данных параллельных прямых, пересекает и другую.

641. В параллелепипеде ABCDA₁B₁C₁D₁ укажите параллельные прямые, на которых лежат его рёбра.

641. В тетраэдре DABC укажите все пары скрещивающихся прямых, на которых лежат его рёбра.

641. В пространстве даны три попарно пересекающиеся прямые. Изобразите возможные случаи их взаимного расположения.

641. Прямая с пересекает, по крайней мере, одну из двух пересекающихся прямых а, b. Как могут располагаться относительно друг друга эти три прямые? Сделайте рисунки.

641. Даны две параллельные прямые а и b. Как может быть расположена по отношению к ним третья прямая c? Сделайте рисунки.

641. Даны две скрещивающиеся прямые а и b. Как может быть расположена по отношению к ним третья прямая c? Сделайте рисунки.

642. Отметьте верные утверждения:

а) прямая, параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости.

б) существует единственная прямая, параллельная данной плоскости и проходящая через точку, не принадлежащую этой плоскости.

в) существует бесконечное множество прямых, параллельных данной плоскости и проходящих через точку, не принадлежащую этой плоскости.

г) через одну из двух параллельных прямых можно провести бесконечное множество плоскостей, параллельных другой прямой.

д) существует единственная плоскость, параллельная данной прямой и проходящая через точку, не принадлежащую этой прямой.

е) существует бесконечное множество плоскостей, параллельных данной прямой и проходящих через точку, не принадлежащую этой прямой.

641. Используя признак параллельности прямой и плоскости, укажите несколько пар параллельных прямой и плоскости в четырёхугольной призме ABCDA₁B₁C₁D₁.

641. Докажите, что в кубе ABCDA₁B₁C₁D₁ прямая AB₁ параллельна плоскости грани DD₁CC₁.

641. Прямые а и b скрещиваются. Можно ли провести через одну из них плоскость, параллельную другой? Обоснуйте свой ответ.

642. Отметьте верные утверждения

а) через точку, не принадлежащую данной плоскости, проходит единственная плоскость, параллельная данной.

б) если прямая, лежащая в одной плоскости, параллельна прямой, лежащей в другой плоскости, то эти плоскости параллельны.

в) если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны.

г) если одна из двух данных плоскостей параллельна двум пересекающимся прямым, лежащим в другой плоскости, то эти плоскости параллельны.

д) если плоскость пересекает две данные плоскости по параллельным прямым, то эти плоскости параллельны.

е) если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

ж) если две плоскости параллельны одной и той же прямой, то они параллельны.

641. Используя признак параллельности плоскостей, укажите параллельные плоскости в прямоугольном параллелепипеде ABCDA₁B₁C₁D₁.

642. PABC – правильный тетраэдр, точка М – центр грани АВС, К – середина ребра АВ. Постройте сечения тетраэдра плоскостями:

а) APM; б) KPM.

Постройте общий отрезок этих сечений.

641. Постройте сечение тетраэдра плоскостью, проходящей через:

а) две вершины и точку на ребре, не содержащем эти вершины;

б) вершину и две точки на рёбрах, не проходящих через эту вершину;

в) три точки на трёх рёбрах, выходящих из одной вершины;

г) середины трёх рёбер, не выходящих из одной вершины.

641. В четырёхугольной пирамиде все рёбра равны. Докажите, что её сечение, проходящее через вершину пирамиды и диагональ основания, является прямоугольным треугольником.

642. Постройте сечение куба плоскостью, проходящей через точку на боковом ребре и две точки на рёбрах основания, не смежных с этим боковым ребром.

643. Постройте сечение куба плоскостью, проходящей через две точки на скрещивающихся рёбрах верхнего и нижнего оснований и точку на ребре:

а) пересекающимся с ними;

б) пересекающимся только с одним из этих рёбер.

641. Постройте сечение четырёхугольной пирамиды плоскостью, проходящей через три точки на боковых рёбрах.

В каждом из нижеследующих заданий найдите площадь построенного сечения, учитывая, что все рёбра всех данных многогранников равны 1.

641. Постройте сечение куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через:

а) середины рёбер АА₁, ВВ₁, В₁С₁;

б) середины рёбер ВВ₁, DD₁ и вершину А;

в) середину ребра C₁D₁ и вершины А, С;

г) середины рёбер АА₁, СС₁ и точку М на ребре АВ такую, что АМ = 0,75.

641. Постройте сечение куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через:

а) середины рёбер ВВ₁, СС₁, А₁В₁;

б) середины рёбер АА₁, СС₁ и вершину В;

в) середину ребра СC₁ и вершины А₁, В;

г) середины рёбер АА₁, СС₁ и точку М на ребре ВВ₁ такую, что ВМ = 0,25.

641. Постройте сечение правильной треугольной пирамиды DABC плоскостью, проходящей через:

а) середины рёбер АВ, ВС и СD;

б) середины рёбер AD, BD и ВС.

641. Постройте сечение правильной четырёхугольной пирамиды MABCD плоскостью, проходящей через:

а) середину ребра МА и вершины В и С;

б) середину ребра МС и вершины А и В;

в) середины рёбер AD, ВC и MD.

641. Постройте сечение правильной треугольной призмы ABCA₁B₁C₁ плоскостью, проходящей через:

а) середины рёбер АВ, ВС и А₁В₁;

б) середину ребра АС и вершины А₁ и В₁;

в) середины рёбер АА₁, ВВ₁ и А₁С₁;

г) середину ребра АС и вершины В и В₁;

д) середину ребра А₁С₁ и вершины А и В.

641. Постройте сечение правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁ плоскостью, проходящей через:

а) вершины А, D и С₁;

б) вершины А, С и D₁;

в) вершины А, В и D₁;

г) вершины B, D и Е₁;

д) вершины С, F и E₁.