
glava5
.pdf
§ 25
Опытное обоснование молекулярно-кинетической теории
1. Броуновское движение. Шотландский ботаник Р.Броун (1773–1858), на-
блюдая под микроскопом взвесь цветочной пыльцы в воде, обнаружил, что части-
цы пыльцы оживленно и беспорядочно двигались, то вращаясь, то перемещаясь с места на место, подобно пылинкам в солнечном луче. Впоследствии оказалось,
что подобное сложное зигзагообразное движение характерно для любых частиц малых размеров (~1 мкм), взвешенных в газе или жидкости. Интенсивность этого движения, называемого броуновским, повышается с ростом температуры среды,
с уменьшением вязкости и размеров частиц. Причина броуновского движения долго оставалась неясной. Лишь через 80 лет после обнаружения этого эффекта ему было дано объяснение: броуновское движение взвешенных частиц вызывает-
ся ударами молекул среды, в которой частицы взвешены. Так как молекулы дви-
жутся хаотически, то броуновские частицы получают толчки с разных сторон, по-
этому и совершают движения столь причудливой формы. Таким образом, бро-
уновское движение является подтверждением выводов молекулярно-
кинетической теории о хаотическом тепловом движении атомов и молекул.
2. Опыт Штерна. Первое экспериментальное определение скоростей молекул выполнено немецким физиком О. Штерном (1888–1970). Его опыты позволя-
ют также оценить распределение молекул по ско-
ростям. Схема установки Штерна представлена на рисунке. Вдоль оси внутреннего цилиндра с щелью
натянута платиновая проволока, покрытая слоем серебра, которая нагревается током при откачанном воздухе. При нагревании серебро испаряется. Атомы се-
ребра, вылетая через щель, попадают на внутреннюю поверхность второго цилин-
дра, давая изображение щели О. Если прибор привести во вращение вокруг общей оси цилиндров, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние s. Изображение щели получится размытым. Исследуя

толщину осажденного слоя, можно оценить распределение молекул по скоростям,
которое соответствует максвелловскому распределению.
Зная радиус цилиндров r и R , а также их угловую скорость вращения ω, и
измеряя s, можно вычислить скорость движения атомов серебра при данной тем-
пературе
t = |
s |
= |
R − r |
– время движения молекул между цилиндрами, |
ωR |
|
|||
|
|
v |
||
v = ωR R − r . s
Результаты опытов показывают, что скорость атомов серебра близка к той, кото-
рая следует из максвелловского распределения молекул по скоростям. 3. Опыт Ламмерта. Этот опыт позво-
ляет более точно определить закон распреде-
ления молекул по скоростям. Схема вакуумной установки представлена на рисунке. Молекулярный пучок, сформиро-
ванный источником, проходя через щель,
попадает в приемник. Между источником и приемником помещают два диска с прорезями, закрепленных на общей оси. При неподвижных дисках молекулы дос-
тигают приемника, проходя через прорези в обоих дисках. Если ось привести во вращение, то приемника достигнут только те прошедшие прорезь в первом диске молекулы, которые затрачивают для пробега между дисками время, равное или кратное времени оборота диска. Другие же молекулы задерживаются вторым дис-
ком. Меняя угловую скорость вращения дисков и измеряя число молекул, попа-
дающих в приемник, можно выявить закон распределения скоростей молекул.
Этот опыт также подтвердил справедливость максвелловского распределения мо-
лекул по скоростям.
4. Опытное определение постоянной Авогадро. Воспользовавшись рас-
пределением молекул по высоте, французский ученый Ж. Перрен (1870–1942)
экспериментально определил постоянную Авогадро. Исследуя под микроскопом

броуновское движение, он убедился, что броуновские частицы распределяются по высоте подобно молекулам газа в поле тяготения. Применив к ним больцманов-
ское распределение, можно записать
n = n0 e−(m−m1 )gh kT ,
kT ,
где m – |
масса частицы, m1 – масса вытесненной ею жидкости: m = 4πρr3 3 , |
|
m = 4πρ r3 |
3 ( r – радиус частицы, ρ – плотность частицы, ρ1 – плотность жид- |
|
1 |
1 |
|
кости).
Если n1 и n2 – концентрации частиц на уровнях h1 и h2 , а k = R NA , то
NA , то
NA = |
3RT ln(n1 n2 ) |
|||
|
|
|
. |
|
4πr3 (ρ −ρ )g(h |
2 |
−h ) |
||
|
1 |
1 |
|
|
Значение NA , получаемое из работ Ж.Перрена, соответствовало значениям,
полученным в других опытах, что подтверждает применимость к броуновским частицам распределения Больцмана.
§ 26
Среднее число столкновений и средняя длина свободного пробега молекул
Расстояние между двумя последовательными столкновениями молекулы l, назы-
вается длиной свободного пробега.
Эффективный диаметр молекулы d – это минимальное расстояние, на которое могут сближаться центры двух молекул в результате столкновения.
Средняя длина свободного пробега молекул равна
< l >= < v > < z >,
< z >,
где < v > – |
средняя арифметическая |
скорость, < z > – |
среднее число столкнове- |
ний, испытываемых одной молекулой газа
за 1 с.
Среднее число столкновений за 1 с равно числу молекул в объеме «ломано-
го» цилиндра

< z >= nV ,
где n – концентрация молекул, V = pd2 < v > . Таким образом, среднее число
столкновений
< z >= npd2 < v > .
Расчеты показывают, что при учете движения других молекул
< z >= 
 2pd2 n < v > .
2pd2 n < v > .
Тогда средняя длина свободного пробега равна
< l >= |
|
1 |
. |
|
|
|
|
||
|
|
2pd2n |
||
Задача 1. Средняя длина свободного пробега молекул кислорода при тем-
пературе 280 К и давлении 0,1 МПа равна 190 нм. Найдите эффективный диаметр молекулы кислорода.
Дано: |
|
|
|
СИ |
|
|
|
|
|
|
Решение |
|||||||
T = 280 К |
|
|
|
|
|
|
|
Средняя длина свободного пробега молекул оп- |
||||||||||
p = 0,1 МПа |
|
105 Па |
ределяется выражением |
|||||||||||||||
l = 190 нм |
|
1,9×10–7 м |
< l >= |
1 |
, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2pd2n |
|||
d = ? |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
где n – |
концентрацию молекул газа определим из фор- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
мулы |
p = nkT . Тогда уравнение для средней длины |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
свободного пробега имеет вид |
|
|
|
|
|
|
||||||||||||
< l >= |
|
|
|
kT |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2pd2p |
|
|
|
|
|
|
|
||||||
где k = 1,38×10−23 Дж/К – |
постоянная Больцмана. Из полученного равенства выра- |
|||||||||||||||||
зим эффективный диаметр молекулы |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
d = |
|
|
|
kT |
|
|
|
|
|
|
|
|||||||
|
|
|
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2pp l |
|
|
|
|
|
|
|
|||||||
В полученную формулу подставим числовые значения |
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||
d = |
|
|
1,38 ×10−23 Дж/К×280 К |
= 2,1×10−10 м = 210 пм. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 ×3,14 ×105 Па×1,9 ×10−7 м |
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||

Задача 2. При каком давлении средняя длина свободного пробега молекул кислорода будет равна 1 мм, если при нормальном давлении она равна 50 нм?
Температура постоянна. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Дано: |
|
|
СИ |
|
|
|
|
|
|
|
|
|
Решение |
|||
l |
|
= 1 мм |
10–3 м |
|
|
Средняя длина свободного пробега молекул опре- |
||||||||||
l |
|
= 50 нм |
5 10–8 |
м |
деляется выражением |
|||||||||||
|
0 |
|
|
× |
|
|
|
|
|
|
|
|
|
|
||
p0 = 105 Па |
|
|
|
|
|
< l >= |
|
1 |
|
|
, |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
2pd |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||
p = ? |
|
|
|
|
|
где n – |
концентрацию молекул газа определим из форм- |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
мулы |
p = nkT . |
|
Тогда уравнение для средней длины |
||||
|
|
|
|
|
|
|
|
|
|
|||||||
свободного пробега имеет вид |
|
|
|
|
|
|
|
|||||||||
|
|
< l >= |
|
|
kT |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2pd2p |
|
|
|
|
|
|
|
|
|||
где k = 1,38×10−23 Дж/К – постоянная Больцмана, d – эффективный диаметр мо-
лекулы. Запишем, по аналогии, выражение для средней длины свободного пробе-
га молекулы при нормальных условиях
< l0 |
>= |
|
kT0 |
. |
|||
|
|
|
2p0 |
||||
2pd |
|||||||
|
|
|
|
||||
Найдем отношение этих формул с учетом того, что T = T0
 l
l = p0 .
= p0 .  l0
l0  p
p
Из полученного равенства выразим давление
p = p0  l0
l0  l
l
и подставим числовые значения
p = 105 Па× 5 ×10−8 м = 5 Па . 10−3 м

Задача 3. Средняя длина свободного пробега молекулы углекислого газа при нормальных условиях равна 35 нм. Найдите число соударений, которые ис-
пытывает молекула в 1 с. Молярная масса углекислого газа равна 0,044 кг/моль.
Дано: |
|
|
|
|
|
|
|
|
|
СИ |
|
|
|
|
|
|
|
Решение |
||||
l = 35 нм |
|
|
|
|
|
|
|
3,5×10–8 |
м |
|
Средняя длина свободного пробега молекул |
|||||||||||
M = 0,044 кг/моль |
|
|
|
|
|
|
|
и среднее число соударений в единицу времени |
||||||||||||||
T = 273 К |
|
|
|
|
|
|
|
|
|
|
|
|
|
связаны между собой соотношением |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
z = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
= |
, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
v |
– средняя арифметическая скорость моле- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
кул газа, которая равна |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = |
8RT |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
pM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставим эту формулу в первое равенство, получим |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z = |
1 |
|
|
|
8RT |
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
l |
|
|
|
pM |
|
|
|
|
|
|
|
|
|||||||||
После подстановки числовых значений получаем |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
z = |
|
|
1 |
|
|
|
|
|
× |
|
8 ×8,31 Дж/(моль× К) × 273 К |
|
= 1010 с−1 . |
|||||||||
3,5 ×10−8 |
|
|
|
|
||||||||||||||||||
|
м |
3,14 ×0,044 кг/моль |
|
|
|
|||||||||||||||||
Задача 4. Сколько столкновений за одну секунду испытывает молекула не-
она при температуре 400 К и давлении 133 Па, если ее эффективный диаметр 204
пм? Молярная масса неона равна 0,004 кг/моль. |
|
||||
|
|
|
|
|
|
Дано: |
СИ |
|
|
|
Решение |
d = 204 пм |
2,04×10–10 м |
Среднее число соударений молекулы в |
|||
T = 400 К |
|
единицу времени определяется соотношением |
|||
p =133 Па |
|
z |
= |
v |
, |
|
|
||||
M = 0,004 кг/моль |
|
l |
|||
|
|
|
|
||
|
|
|
|
||
z = ? |
|
где v – |
средняя арифметическая скорость, |
||
|
|
|
|
|
|

 l
l – средняя длина свободного пробега молекул газа, которые, соответственно,
– средняя длина свободного пробега молекул газа, которые, соответственно,
равны
v = |
8RT |
и < l >= |
|
|
1 |
. |
|
|
|
|
|||
|
pM |
2pd2n |
||||
Подставим эти выражения в первую формулу
 z
z = 2pd2n 8RT = d2n 4pRT , pM M
= 2pd2n 8RT = d2n 4pRT , pM M
где n – концентрация молекул, которую выразим из равенства p = nkT и учтем,
что постоянная Больцмана и универсальная газовая постоянная связаны между собой формулой R = kNA . С учетом этого преобразуем выражение для 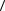 z
z
z = d2 |
p |
|
|
4pkNAT |
|
= 2pd2 |
|
pNA |
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
||||||||||
|
kT |
|
|
M |
MkT |
|
|
|
|
|||||||
Подставим числовые значения |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z = 2 ×133 Па×(2,04 ×10−10 м)2 × |
|
|
3,14 ×6,02 ×1023 моль |
−1 |
= 3,2 ×106 с−1 . |
|||||||||||
0,004 кг/моль×1,38×10−23 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
Дж/К× 400 К |
||||||||
§ 27
Явления переноса в термодинамически неравновесных системах
Особые необратимые процессы в результате которых происходит пространствен-
ный перенос энергии, массы, импульса, называются явлениями переноса.
К явлениям переноса относятся:
1)теплопроводность (обусловлена переносом энергии);
2)диффузия (обусловлена переносом массы);
3)внутреннее трение (обусловленное переносом импульса).
1.Теплопроводность. Перенос энергии в форме теплоты подчиняется за-
кону Фурье
j |
|
= −λ |
dT |
, |
(27.1) |
Q |
|
||||
|
|
dx |
|
||
|
|
|
|
||
где jQ – |
плотность теплового потока – |
величина, определяемая энергией, пере- |
|||
носимой в форме теплоты в единицу времени через единичную площадку, пер-
пендикулярную оси X; λ – теплопроводность (коэффициент теплопроводности); dT dx – градиент температуры, равный скорости изменения температуры на единицу длины вдоль оси X в направлении нормали к этой площадке.
dx – градиент температуры, равный скорости изменения температуры на единицу длины вдоль оси X в направлении нормали к этой площадке.
Теплопроводность λ числено равна плотности теплового потока при градиенте температуры, равном единице.
Можно показать, что
λ = |
1 |
c |
|
ρ < v >< l > , |
(27.2) |
|
V |
||||
3 |
|
|
|||
где cV – удельная теплоемкость газа при постоянном объеме, ρ – |
плотность газа. |
||||
2. Диффузия. Явление диффузии заключается в том, что происходит са-
мопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и твердых тел. Явление диффузии для химически однородного газа подчиняется закону Фика
j |
|
= −D |
dρ |
, |
(27.3) |
m |
|
||||
|
|
dx |
|
||
|
|
|
|
||
где jm – |
плотность потока массы – |
величина определяемая массой вещества, |
|||
диффундирующего в единицу времени через единичную площадку, перпендику-
лярную оси X; D – диффузия (коэффициент диффузии); dρ dx – градиент плот-
dx – градиент плот-
ности, равный скорости изменения плотности на единицу длины вдоль оси X в
направлении нормали к этой площадке.
Диффузия D числено равна плотности потока массы при градиенте плотности,
равном единице.
D = |
1 |
|
< v >< l >. |
(27.4) |
|||
|
|||||||
3 |
|
|
|
|
|||
3. Внутреннее трение (вязкость). Сила внутреннего трения между двумя |
|||||||
слоями газа или жидкости подчиняется закону Ньютона |
|
||||||
|
dv |
|
|
|
|||
F = η |
|
|
S , |
(27.5) |
|||
dx |
|||||||
|
|
|
|
|
|||
где η – динамическая вязкость (вязкость); dv dx – градиент скорости, показы-
dx – градиент скорости, показы-
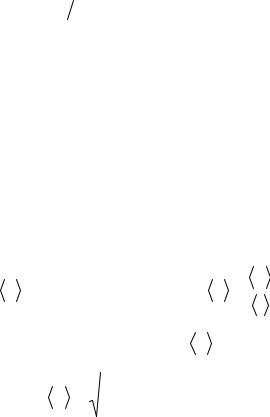
вающий быстроту изменения скорости в направлении оси X, перпендикулярном направлению движения слоев; S – площадь, на которую действует сила F .
Взаимодействие двух слоев можно представить как процесс передачи им-
пульса от одного слоя к другому в единицу времени. Тогда выражение (27.5) мож-
но представить в виде
jp |
= -h |
dv |
, |
(27.6) |
|
||||
|
|
dx |
|
|
где jp – плотность потока импульса – величина определяемая полным импуль-
сом, переносимым в единицу времени в положительном направлении оси X через единичную площадку, перпендикулярную этой оси; dv dx – градиент скорости.
dx – градиент скорости.
Динамическая вязкость h числено равна плотности потока импульса при гради-
енте скорости, равном единице.
h = |
1 |
r < v >< l > . |
(27.7) |
|
|||
3 |
|
||
Из формул (27.2), (27.4) и (27.7) вытекает взаимосвязь между теплопровод-
ностью, диффузией и динамической вязкостью
h = rDl hc = .
V 1
Задача 1. Определите среднее число столкновений молекул кислорода за секунду при нормальных условиях, если коэффициент вязкости кислорода при
этих условиях 2,0×10–5 Па×с. |
|
|
|
|||||
Дано: |
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|||
p = 105 Па |
|
|
|
Среднее число столкновений молекулы за единицу |
||||
h = 2,0 ×10−5 Па × с |
времени определяется выражением |
|||||||
|
|
|
|
|
|
= |
v |
|
z = ? |
|
|
|
z |
, |
|||
|
|
|
l |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где v – |
средняя арифметическая скорость молекул, равная |
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
v = |
8RT |
; |
|
|
|
|
||
|
|
|
|
|
||||
|
|
pM |
|
|
|
|
||
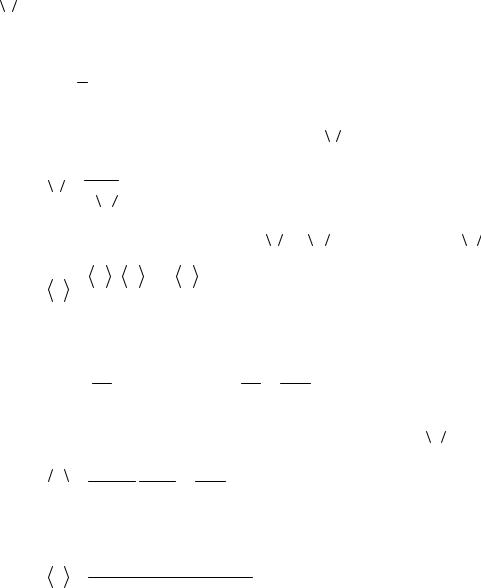
 l
l – средняя длина свободного пробега молекул, для определения которой запи-
– средняя длина свободного пробега молекул, для определения которой запи-
шем формулу для коэффициента вязкости газа
h = 1 r < v >< l > , 3
где r – плотность газа. Выразим отсюда  l
l
 l
l = 3η . ρ
= 3η . ρ v
v
Подставим выражения для  l
l и
и  v
v в формулу для
в формулу для  z
z
z = |
v ρ v |
= |
ρ v 2 |
= |
ρ |
|
8RT |
. |
3η |
3η |
|
|
|||||
|
|
|
3η πM |
|||||
Плотность газа выразим из уравнения Клапейрона-Менделеева
pV = m RT , откуда ρ = m = pM . M V RT
Подставим выражение для плотности в формулу для  z
z
= pM 8RT = 8p  z
z 3hRT pM 3ph .
3hRT pM 3ph .
Подставим числовые значения
z = |
8 ×105 Па |
= 4,2 ×109 с−1 . |
3×3,14 ×2,0 ×10−5 Па×с |
Задача 2. Найдите коэффициент теплопроводности воздуха при нормаль-
ных условиях. Эффективный диаметр молекулы воздуха 0,30 нм.
Дано: |
СИ |
|
|
|
|
Решение |
d = 0,30 нм |
3×10–10 м |
Коэффициент теплопроводности газа опре- |
||||
T = 273 К |
|
деляется по формуле |
||||
M = 0,029 кг/моль |
|
l = |
1 |
c |
|
r < v >< l > , |
|
|
|
V |
|||
i = 5 |
|
3 |
|
|||
|
|
|
|
|
|
|
|
|
где cV – удельная теплоемкость газа при постоян- |
||||
λ = ? |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
