
glava5
.pdfРаздел II
ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Введение
Макроскопической называется система, образованная огромным числом микро-
частиц (молекул, атомов, ионов, электронов).
Для изучения процессов, происходящих в макроскопических системах,
применяют два качественно различных и взаимно дополняющих друг друга мето-
да: статистический (молекулярно-кинетический) и термодинамический. Пер-
вый лежит в основе молекулярной физики, второй – термодинамики. Молекулярная физика – раздел физики, изучающий строение и свойства веще-
ства исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.
Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистической физики.
Статистический метод основан на том, что свойства макроскопической сис-
темы, в конечном счете, определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц.
Термодинамика – раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями.
Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистическо-
го. Термодинамика базируется на двух началах – фундаментальных законах, уста-
новленных в результате обобщения опытных данных.
Термодинамическая система – совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими те-
лами (внешней средой).
Основа термодинамического метода – определение термодинамического со-
стояния системы, которое задается термодинамическими параметрами.
Термодинамические параметры (параметры состояния) – совокупность физи-
ческих величин, характеризующих свойства термодинамической системы.
Обычно в качестве термодинамических параметров выбирают температуру
T , давление p и объем V (удельный объем v).
Температура – физическая величина, характеризующая состояние термодинами-
ческого равновесия макроскопической системы.
В Международной практической шкале температура замерзания и кипе-
ния воды при p = 1,013×105 Па соответственно 0°С и 100°С (так называемые ре-
перные точки). Термодинамическая температурная шкала определяется по од-
ной реперной точке, в качестве которой взята тройная точка воды (температура,
при которой лед, вода и насыщенный пар при p = 609 Па находятся в термодина-
мическом равновесии) Tmm = 273,16 К, T =1K = t =1°C . Температура замерза-
ния воды равна T = 273,15 К.
T= 273,15 + t .
ВСША применяется температурная шкала Фаренгейта. По ней температура
замерзания воды – tз |
= 0°C = 32°F , а температура кипения – tк =100°C = 212°F . |
||||
Удельный объем v – |
это объем единицы массы вещества. |
||||
v = |
V |
= |
1 |
. |
|
|
|
|
|||
|
m r |
|
|||
Любое изменение термодинамической системы, связанное с изменением хотя бы одного из ее термодинамических параметров, называется термодинамическим процессом.
Макроскопическая система находится в термодинамическом равновесии, если ее состояние с течением времени не изменяется.

Глава 5 Молекулярно-кинетическая теория идеального газа
§ 20
Опытные законы идеального газа Идеальный газ – это идеализированная модель, согласно которой: 1) собствен-
ный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) между молекулами газа отсутствуют силы взаимодействия; 3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Закон Бойля-Мариотта. Для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная.
pV = const , |
(20.1) |
при T = const и m = const . Процесс, проходящий при T = const , называется изотермическим. Кривые,
изображающие зависимость между величинами p и V , характеризующими свой-
ства вещества при постоянной температуре, называются изотермами. Закон Гей-Люссака. Отношение объема данной массы газа при постоянном давлении к его термодинамиче-
ской температуре есть величина постоянная.
V |
= const , |
(20.2) |
|
||
T |
|
|
при p = const и m = const . Процесс, протекающий при
постоянном давлении, называется изобарным. Прямая, изображающая этот про-
цесс – изобарой.
Закон Шарля. Отношение давления данной массы газа при постоянном объеме к его термодинамической температуре есть величина постоянная.
p |
= const , |
(20.3) |
|
T
при V = const и m = const . Процесс, протекающий при постоянном объеме, называется изохорным. Прямая изображающая этот процесс – изохорой.
Закон Авогадро. Моли любых газов при одинаковой температуре и давлении за-
нимают одинаковые объемы.
При нормальных условиях V0m = 22,41×10−3 м3 моль. По определению, в
моль. По определению, в
одном моле различных веществ содержится одно и тоже число молекул, которое называется числом Авогадро
NA = 6,022 ×1023 моль-1 .
Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов
n
p= p1 + p2 +... + pn = ∑pi ,
i=1
где p1 , p2 , …, pn – парциальные давления – давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
§ 21
Уравнение Клапейрона– Менделеева
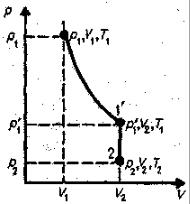
Между параметрами p , V и T , определяющими состояние некоторой мас-
сы газа, существует определенная связь, называемая уравнением состояния, ко-
торое в общем виде задается выражением f(p, V,T) = 0 ,
где каждая из переменных является функцией двух других.
Французский физик и инженер Б. Клапейрон |
|
(1799–1864) вывел уравнение состояния идеального газа. |
|
В соответствии с газовыми законами запишем |
|
p1V1 = p1′V2 , |
(21.1) |
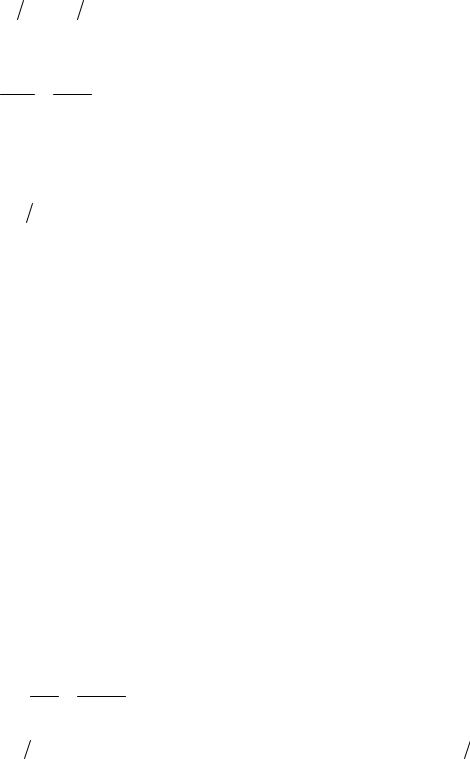
′ |
p2 = T1 T2 . |
(21.2) |
p1 |
Исключив из уравнений (21.1) и (21.2) p′ , получим
1
p1V1 = p2 V2 . T1 T2
Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа величина pV T – остается постоянной, т.е.
T – остается постоянной, т.е.
pV T = B = const . |
(21.3) |
Выражение (52.3) является уравнением Клапейрона, в котором B – |
газовая по- |
стоянная, различная для разных газов. |
|
Д.И. Менделеев (1834–1907) объединил уравнение Клапейрона с законом
Авогадро, отнеся уравнение (52.3) к одному молю, и использовав молярный объ-
ем Vm . Из закона Авогадро следует, что B будет одинаковой для всех газов. Эта общая для всех газов постоянная R и называется молярной газовой постоянной.
Уравнению
pVm = RT |
(21.4) |
удовлетворяет лишь идеальный газ, и оно является уравнением состояния иде-
ального газа, называемое так же уравнением Клапейрона– Менделеева.
pV = νRT , |
(21.5) |
где R = 8,31 Дж/(моль×К), ν = m M – количество вещества, V = νVm – объем газа,
M – количество вещества, V = νVm – объем газа,
M – молярная масса.
p = RT = kNAT = nkT , Vm Vm
где k = R N |
A |
=1,38 ×10−23 |
Дж/К – |
постоянная Больцмана, n = N |
A |
V – концентра- |
|
|
|
|
m |
||
ция молекул. |
|
|
|
|
|
|
p = nkT |
|
|
|
(21.6) |
||
Число молекул в 1 м3 газа при нормальных условиях называется числом
Лошмидта.
NL = p0 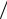 kT0 = 2,68 ×1025 м-3 .
kT0 = 2,68 ×1025 м-3 .

Задача 1. В колбе вместимостью 300 см3 находится газ при температуре 280
К и давлении 40 кПа. Определите количество вещества газа (число молей) и число
его молекул. |
|
|
|
|
|
Дано: |
СИ |
Решение |
V = 300 см3 |
3×10−4 м3 |
Запишем уравнение Клапейрона-Менделеева для |
T = 280 К |
|
состояния идеального газа |
p = 40 кПа |
4 ×104 Па |
pV = νRT , |
|
|
где R = 8,31 Дж/(моль×К) – универсальная газовая по- |
ν = ? N = ? |
|
|
|
стоянная. Выразим отсюда количество вещества |
|
|
|
|
|
|
|
n = pV .
RT
Подставим числовые значения
|
4 ×104 |
Па×3×10-4 |
м3 |
|
n = |
|
|
|
» 0,005 моль. |
8,31 Дж/(моль×К) × |
|
|||
|
280 К |
|||
Количество молекул найдем по формуле
N = νNA ,
где NA = 6,02 ×1023 моль-1 – число Авогадро. Подставим числовые значения
N = 0,005 моль×6,02 ×1023 моль−1 = 3,1×1021 .
Задача 2. Определите плотность воздуха при температуре 290 К. Давление
воздуха равно 95 кПа, молярная масса – 29 г/моль.
Дано: |
СИ |
|
|
Решение |
T = 290 К |
|
Запишем уравнение Клапейрона-Менделеева для |
||
p = 95 кПа |
9,5 ×104 Па |
состояния идеального газа |
||
M = 29 г/моль |
0,029 кг/моль |
pV = |
m |
RT , |
|
|
|||
|
|
|
M |
|
ρ = ? |
|
|
||
|
где R = 8,31 Дж/(моль×К) – универсальная газовая |
|||
|
|
|||
|
|
постоянная, m и V – масса и объем газа, соот- |
||
|
|
|||
ветственно. Разделим обе части уравнения на объем |
||||

p = m RT VM
и, учитывая, что m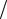 V = ρ плотность газа, выразим ее из уравнения
V = ρ плотность газа, выразим ее из уравнения
r = pM .
RT
Подставив числовые значения, получим
r = 9,5 ×104 Па×0,029 кг/моль = 1,14 кг/м3 . 8,31 Дж/(моль× К) × 290 К
Задача 3. Найдите массу воздуха, заполняющего аудиторию высотой 3,5 м
и площадью пола 150 м2. Давление воздуха 101 кПа, температура в помещении
300 К. Молярная масса воздуха 0,029 кг/моль.
Дано: |
|
|
|
|
СИ |
|
|
|
Решение |
|
h = 3,5 м |
|
|
|
|
|
|
Запишем уравнение Клапейрона-Менделеева для |
|||
S = 150 м2 |
|
|
|
|
|
|
состояния идеального газа |
|||
p = 101кПа |
|
1,01×105 Па |
pV = |
m |
RT , |
|
||||
|
|
|||||||||
M = 0,029 кг/моль |
|
|
|
|
M |
|
||||
|
|
|
где R = 8,31 Дж/(моль×К) – универсальная газо- |
|||||||
T = 300 К |
|
|
|
|
|
|
||||
|
|
|
|
|
|
вая постоянная, V = Sh – объем воздуха. |
||||
|
|
|
|
|
|
|
||||
m = ? |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выразим из уравнения массу воздуха |
|||
|
|
|
|
|
|
|
||||
m = |
pMV |
= |
pMSh |
. |
|
|
|
|
||
|
|
|
|
|
|
|||||
|
|
RT |
|
RT |
|
|
|
|
||
Подставим числовые значения в полученное равенство |
||||||||||
m = |
1,01×105 |
Па×0,029 кг/моль×150 м2 ×3,5 м |
» 617 кг . |
|||||||
|
|
8,31 Дж/(моль×К) ×300 К |
||||||||
|
|
|
|
|||||||

§ 22
Основное уравнение молекулярно-кинетической теории идеальных газов
Для вывода основного уравнения молекулярно-кинетической теории рас-
смотрим одноатомный идеальный газ. Предположим, что:
1)молекулы газа движутся хаотически;
2)число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда;
3)соударения молекул со стенками сосуда абсолютно упругие.
Выделим на стенке сосуда некоторую элементарную площадку S и вычислим давление, оказываемое на эту
площадку.
m0v − (−m0v) = 2m0v – импульс получаемый стен-
кой при каждом соударении молекулы, движущихся перпендикулярно площадке
S .
N = n Sv t – число молекул попадающих на площадку S за время t
( n – концентрация молекул). Из всех молекул N , находящихся в объеме Sv t ,
на площадку S движется только шестая их часть. Таким образом, при столкно-
вении с площадкой |
S эти молекулы передадут ей импульс |
|||
DP = 2m0v × |
1 |
nDSvDt = |
1 |
nm0v2DSDt . |
|
|
|||
6 |
3 |
|||
Известно, что P = F t = p S t . Тогда давление, оказываемое газом на стенку
сосуда равно
p = |
P |
= |
1 |
nm0v2 . |
(22.1) |
DSDt |
|
||||
|
3 |
|
|||
Если газ в объеме V содержит N молекул, движущихся со скоростями v1 , v2 , …, vN , то целесообразно рассматривать среднюю квадратичную скорость
|
1 |
N |
|
|
vкв = |
∑vi2 , |
(22.2) |
||
|
||||
|
N i=1 |
|
||
характеризующую всю совокупность молекул газа. Тогда уравнение (22.1) с уче-
том (22.2) примет вид

p = |
1 |
nm |
|
< v2 |
> . |
(22.3) |
|
0 |
|||||
3 |
кв |
|
|
|||
|
|
|
|
|||
Выражение (22.3) |
называется основным уравнением |
молекулярно- |
||||
кинетической теории идеального газа.
Учитывая, что n = N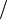 V , получим
V , получим
pV = |
1 |
Nm |
|
|
< v2 |
> |
|
|
|
(22.4) |
||
|
0 |
|
|
|
||||||||
|
3 |
|
|
кв |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
pV = |
2 |
|
m |
0 |
< v2 |
> |
= |
2 |
E , |
(22.5) |
||
|
|
N |
|
|
кв |
|
|
|||||
3 |
|
|
|
2 |
|
3 |
||||||
|
|
|
|
|
|
|
|
|
||||
где E – суммарная кинетическая энергия поступательного движения всех моле-
кул газа. С учетом m = m0N , получим
pV = 1 m < vкв2 > . 3
Для одного моля газа m = M получим
pVm = 1 M < vкв2 > .
3
С другой стороны pVm = RT , тогда
RT = 1 M < vкв2 > ,
3
откуда
< v |
|
|
>= |
|
|
3RT |
. |
|
|
|
|
|
|
|
|
|
|
(22.6) |
||||
кв |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как M = m0NA , из уравнения (22.6) следует, что |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
< v |
|
|
>= |
|
|
3RT |
|
= |
|
|
3kT |
, |
(22.7) |
|||||||||
кв |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
m0NA |
|
|
m0 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где k = R NA – |
постоянная Больцмана. |
|
||||||||||||||||||||
Средняя кинетическая энергия поступательного движения одной молекулы |
||||||||||||||||||||||
идеального газа равна |
|
|
|
|
|
|
|
|
|
|||||||||||||
< ε0 |
>= |
E |
= |
m |
0 |
< v2 |
> |
= |
3 |
kT . |
(22.8) |
|||||||||||
|
|
|
|
кв |
|
|
|
|
|
|
||||||||||||
N |
|
|
|
2 |
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

Задача 1. Найдите концентрацию молекул углекислого газа, молярная мас-
са которого равна 0,044 кг/моль, если их средняя квадратичная скорость равна 300
м/с, а давление 4×104 Па.
Дано: |
|
|
|
Решение |
vкв = 300 м/с |
Запишем основное уравнение молекулярно-кинетической |
|||
M = 0,044 кг/моль |
теории идеального газа |
|||
p = 4 ×104 Па |
p = |
1 |
nm0 vкв |
2 , |
|
||||
|
3 |
|
||
n = ? |
|
|
|
|
|
|
|
|
|
где m0 – масса одной молекулы газа, которая определяется по формуле m0 = M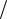 NA . Тогда давление газа будет равно
NA . Тогда давление газа будет равно
p = 1 n M 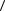 vкв
vкв 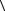 2 .
2 .
3 NA
Из полученного равенства выразим концентрацию молекул
n = 3pNA . M vкв
vкв  2
2
Подставим числовые значения
n = 3× 4 ×104 Па×6,02 ×1023 моль-1 = 1,8 ×1025 м−3 . 0,044 кг/моль×(300 м/с)2
Задача 2. Найдите число молекул кислорода, содержащихся в сосуде объе-
мом 3 л, если средняя квадратичная скорость движения молекул 400 м/с, а давле-
ние в сосуде 2 кПа. Молярная масса кислорода равна 0,032 кг/моль.
Дано: |
СИ |
|
|
|
Решение |
V = 3 л |
0,003 м3 |
Запишем основное уравнение молекулярно- |
|||
vкв = 400 м/с |
|
кинетической теории идеального газа |
|||
p = 2 кПа |
2 ×103 Па |
p = |
1 |
nm0 vкв |
2 , |
|
|||||
M = 0,032 кг/моль |
|
3 |
|
||
|
где m0 – масса одной молекулы газа, которая оп- |
||||
|
|
||||
|
|
ределяется по формуле m0 = M NA . |
|||
N = ? |
|
||||
|
|
|
|
|
|
