Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ухтинский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

glava6

.pdf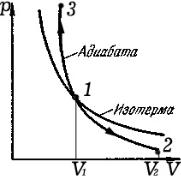

Скачиваний:

Добавлен:

02.03.2016

Размер:

717.37 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

pVγ = const .

(34.4)

Полученное выражение есть уравнение адиабатического процесса, назы-

ваемое также уравнением Пуассона.

Для перехода к переменным T, V или p, T, исключив из (34.4) с помощью

уравнения Клапейрона-Менделеева, соответственно давление или объем

TVγ −1 = const ,	(34.5)
Tγ p1− γ = const .	(34.6)

Выражения (34.4) – (34.6) представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина

γ =	Cp	=	cp	=	i + 2	(34.7)
	CV		cV		i

называется показателем адиабаты (коэффициентом Пуассона).

Диаграмма адиабатического процесса (адиабата)

изображена на рисунке. Вычислим работу, совершенную газом в этом процессе. Запишем уравнение (34.2) в виде

δA = −		m		C	dT .

		M		V

Если газ адиабатически расширяется от объема V1								до V2 ,
то его температура уменьшается от T1 до T2 и работа расширения идеального газа
				T2
A = −	m		CV ∫ dT =			m	CV (T1 − T2 ) .	(34.8)

	M					M
				T1

Применяя те же приемы, что и при выводе формулы (34.5), выражение

(34.8) для работы при адиабатическом расширении можно преобразовать к виду

p V

γ −1

RT m

γ −1

A =

1 1

−

γ −1

γ −1 M

где p1V1 = (mM)RT1 .

Процессы, в которых теплоемкость остается постоянной, называются политроп-

ными.

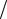
Исходя из I начала термодинамики при условии постоянства теплоемкости

( C = const ) можно вывести уравнение политропы

pVn = const ,

(34.9)

где n = (C −Cp )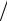(C −CV ) – показатель политропы. Очевидно, что из (34.9) при

C = 0 ,	n = γ	–	получаем уравнение адиабаты;
C = ∞,	n =1	–	уравнение изотермы;
C = Cp , n = 0		–	уравнение изобары;
C = CV , n = ±∞ –			уравнение изохоры.

Таким образом, все рассмотренные изопроцессы являются частными слу-

чаями политропного процесса.

Задача 1. Два моля гелия, находившегося при температуре 300 К, адиабати-

чески сжали так, что его давление возросло в 8 раз. Найдите температуру газа по-

сле сжатия и работу, совершенную над газом.

Дано:

Решение

ν = 2 моля

Запишем уравнение адиабатического процесса через давле-

i = 3

ние и температуру

T1 = 300 К

Tγp1−γ

= Tγp1−γ .

p2 p1 = 8

Преобразуем равенство, переведя температуры в левую часть, а

давления –

T2 = ?

A = ?

в правую

1−γ

γ−1

Выразим отсюда конечную температуру

γ−1

T = T

2 1

где γ –

показатель адиабаты, который равен

γ =

i + 2

Выразим степень полученного равенства через число степеней свободы

γ −1	=	(i + 2 − i)i	=	2
g		i(i + 2)		i + 2

Тогда формула для конечной температуры будет иметь следующий вид

			2
	p
		2		i+2
T2

	= T1		.
	p1

Подставим числовые значения

T2 = 300 К×82(3+2) = 698 К .

Работу, совершенную над газом в адиабатическом процессе, определим по

формуле

A = CVν(T2 −T1 ) ,

где CV – молярная теплоемкость газа при постоянном объеме, которая равна

CV = i R . 2

С учетом этого работа будет равна

A = i nR(T2 - T1 ) . 2

Подставим числовые значения

A= 3 × 2 моля×8,31 Дж/(моль× К) ×(698 К - 300 К) = 9700 Дж. 2

Задача 2. При адиабатическом сжатии 2 кг углекислого газа была затрачена работа 150 кДж. Найдите конечную температуру газа, если он в начале находился

при температуре 273 К.

Дано:	СИ						Решение
m = 2 кг		Работа адиабатического сжатия газа опре-
M = 0,044 кг/моль		деляется по формуле
i = 6		A = C				m	(T - T ) ,
		A = C					(T - T ) ,
A =150 кДж	1,5×105 Дж			V M 2 1
T1 = 300 К		где CV –	молярная теплоемкость газа при посто-
T1 = 300 К
		янном объеме, равная
T2 = ?		янном объеме, равная
T2 = ?
		C	=	i	R .
				i

		V	2
			2

Подставим выражение для теплоемкости в формулу для работы, получим

A = i m R(T2 - T1) . 2 M

Отсюда выразим температуру газа после сжатия

T =	2AM	+ T .
T =		+ T .
2	imR	1
	imR
Подставим числовые значения
T =	2 ×1,5 ×105 Дж×0,044 кг/моль		+ 273	К = 405	К .
T =			+ 273	К = 405	К .
2	6 × 2 кг×8,31 Дж/(моль× К)
	6 × 2 кг×8,31 Дж/(моль× К)

Задача 3. Некоторую массу водорода сжали в 6 раз один раз адиабатически,

другой раз изотермически. Начальное состояние газа в обоих случаях одинаково.

Найдите отношение работы, затраченной на сжатие при адиабатическом процессе,

к соответствующей работе при изотермическом процессе.

Дано:		Решение
γ =1,4		На рисунке изображены графики двух процессов, совершае-
V1	V2 = 6	мых над газом. Процесс 1–2 соответствует адиабатическому сжа-
		тию, процесс 1–3 показывает изотермическое сжатие.
A	A = ?	тию, процесс 1–3 показывает изотермическое сжатие.
12	13

Работа, которая совершается над газом при адиабатическом сжатии, определяется формулой

	m RT			V	γ−1
A =	m RT			V		−1 ,
		1		1			где
	M γ −1						где
12	M γ −1		V
				2

m– масса газа, M – молярная масса, R –

универсальная газовая постоянная.

Работа, совершаемая над газом при изотермическом сжатии равна

		=	m		V
A	23			RT ln	1	.
A				RT ln		.
			M	1	V2
			M		V2

Найдем отношение работы, затраченной на сжатие при адиабатическом процессе,

к соответствующей работе при изотермическом процессе

(V V )γ−1

−1

(γ −1) ln(V V )

Подставим числовые значения

(6)1,4−1 −1

=16 .

A23

(1,4 −1) ln 6

Задача 4. Двухатомный идеальный газ совершает процесс, описываемый

уравнением pV2,5

= const. Найдите молярную теплоемкость газа в этом полит-

ропном процессе.

Дано:

Решение

i = 5

Запишем формулу для показателя политропы

n = 2,5

n =

C −Cp

C −CV

C = ?

где C =

i + 2

R – молярная теплоемкость газа при постоянном давлении,

CV = i R – молярная теплоемкость газа при постоянном объеме. 2

Выразим из формулы для показателя политропы молярную теплоемкость газа в рассматриваемом процессе

C = nCV −Cp . n -1

В полученную формулу подставим выражения для Cp и CV

C = niR - (i + 2)R = (n -1)i - 2 R. 2(n -1) 2(n -1)

Подставим числовые значения

C = (2,5 -1) ×5 - 2 ×8,31 Дж/(моль×К) = 15,2 Дж/(моль× К) . 2 ×(2,5 -1)

§ 35

Круговой процесс (цикл). Обратимые и необратимые процессы

Круговым процессом (циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное.

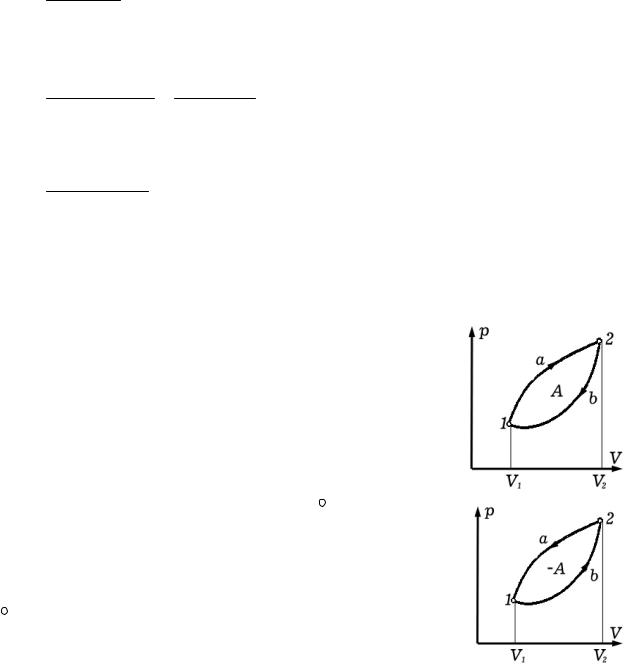
Работа, совершаемая газом за цикл, определяется площадью, охватываемой замкнутой кривой. Если за цикл

совершается	положительная работа		A = ∫pdV > 0	(цикл
протекает по часовой стрелке), то он называется прямым.
Если	за	цикл совершается	отрицательная	работа
A = ∫pdV < 0		(цикл протекает против часовой стрелки), то

он называется обратным.

Прямой цикл используется в тепловых двигателях, а обратный – в холо-

дильных машинах.

Первое начало термодинамики для цикла можно записать в следующем ви-

де ( U = 0 )

Q = U + A = A .

(35.1)

Однако, в результате цикла система может теплоту, как получать, так и отдавать,

поэтому

Q = Q1 − Q2 ,

где Q1 – количество теплоты, полученное системой, Q2 – количество теплоты, от-

данное системой. Поэтому термический коэффициент полезного действия для

кругового процесса

η =	A	=	Q1 − Q2	= 1−	Q2	.	(35.2)

	Q1		Q1		Q1

Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, причем если такой процесс сначала происходит в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит ни-

каких изменений.

Всякий процесс, не удовлетворяющим условиям обратимого, является необрати-

мым.

Обратимые процессы – это идеализация реальных процессов.

§ 36

Энтропия, ее статистическое толкование

и связь с термодинамической вероятностью

Отношение теплоты Q, полученной телом в изотермическом процессе, к темпера-

туре T теплоотдающего тела, называется приведенным количеством теплоты.

Для любого обратимого кругового процесса

∫ T	(36.1)
δQ = 0 .

Из равенства нулю интеграла (36.1) следует, что подынтегральное выраже-

ние δQ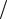T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это со-

стояние. Таким образом,

δQ = dS .	(36.2)
T

Функция состояния, дифференциалом которой является δQT , называется энтро-

пией и обозначается S.

Из формулы (36.1) следует, что для обратимых процессов изменение энтро-

пии
DS = 0 .	(36.3)

В термодинамике доказывается, что энтропия системы, совершающей необрати-

мый цикл, возрастает

DS > 0 .

(36.4)

Выражения (36.3) и (36.4) относятся только к замкнутым системам, если

же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотношения (36.3) и (36.4) можно представить в виде не-

равенства Клаузиуса

DS ³ 0 ,

(36.5)

т.е. энтропия замкнутой системы может либо возрастать, либо оставаться посто-

янной.

Если система совершает равновесный переход из состояния 1 в состояние 2,

то, согласно I начала термодинамики, изменение энтропии равно

S	= S − S =	2	δQ =	2	dU + δA	.	(36.6)
		∫		∫
1→2	2 1		T		T

		1		1

Формула (36.6) определяет энтропию лишь с точностью до аддитивной постоян-

ной. Физический смысл имеет не сама энтропия, а разность энтропий.

Исходя из выражения (36.6), найдем изменение энтропии в процессах иде-

ального газа. Так как

dU =

dT и δA = pdV =

, то

S1→2 = S2 − S1 =

V2 dV

CV T∫

RV∫

или

S1→2 = S2 − S1 =	m		T2	+ Rln	V2
						,	(36.7)
		CV ln
			T1		V1
	M
т.е. изменение энтропии		S1→2 идеального газа при переходе его из состояния 1 в
состояние 2 не зависит от вида процесса перехода 1 – 2 .
Так как для адиабатического процесса δQ = 0 , то							S = 0 и, следовательно,

S = const , т.е. адиабатический обратимый процесс протекает при постоянной эн-

тропии. Поэтому его часто называют изоэнтропийным процессом. Из формулы

(36.7) следует, что при изотермическом процессе (T1 = T2 )

S= m Rln V2 , M V1

при изохорном процессе ( V1 = V2 )

S= m CV ln T2 . M T1

Энтропия обладает свойством аддитивности: энтропия системы равна сум-

ме энтропий тел, входящих в систему

S = ∑Si .

i=1

Более глубокий смысл энтропии вскрывается в статистической физике, эн-

тропия связывается с термодинамической вероятностью состояния системы.

Термодинамическая вероятность W состояния системы – это число способов,

которыми может быть реализовано данное состояние макроскопической системы,

или число микросостояний, осуществляющих данное макросостояние ( W ³ 1).

Согласно Больцману, энтропия S системы и термодинамическая вероят-

ность связаны между собой следующим образом

S = k ln W .

(36.8)

Следовательно, энтропия может рассматриваться как мера вероятности состоя-

ния термодинамической системы.

По Больцману: энтропия является мерой неупорядоченности системы.

Все процессы в реальной замкнутой системе ведут к увеличению ее энтро-

пии – принцип возрастания энтропии.

Задача 1. Найдите изменение энтропии при изотермическом расширении

азота массой 14 г от объема 20 л до объема 80 л.

Дано:

СИ

Решение

M = 0,028 кг/моль

Изменение

энтропии при изотермическом

m =14 г

0,014 кг

процессе определяется по формуле

V1 = 20 л

0,02 м3

DS =

Rln

V2 = 80 л

0,08 м

Подставим числовые значения

S = ?

0,08 м3

0,014 кг

DS =

×8,31 Дж/(моль× К) ×ln

= 5,7 Дж/К .

0,028 кг/моль

0,02 м

Задача 2. Найдите приращение энтропии двух молей углекислого газа при увеличении его абсолютной температуры в 1,5 раза, если процесс нагревания изо-

хорный. Газ считать идеальным.

Дано:						Решение
ν = 2 моля	Изменение энтропии при изохорном процессе равно
i = 6	DS =	m	CV ln		T2	,
	DS =		CV ln			,
T2 T1 =1,5		M			T
T2 T1 =1,5				1
				1
	где m M = ν –			количество вещества, CV – молярная теплоемкость
S = ?	где m M = ν –			количество вещества, CV – молярная теплоемкость
	газа при постоянном объеме, которая определяется по формуле
	газа при постоянном объеме, которая определяется по формуле

CV = i R . 2

Подставим в формулу для изменения энтропии выражение для молярной тепло-

емкости, и отношение массы газа к молярной массе заменим на количество веще-

ства, тогда получим

DS =	i	T
			2

	2 nRln		T	.
			1

Подставим числовые значения

DS = 6 × 2 моля×8,31 Дж/(моль× К) ×ln1,5 = 20 Дж/К.

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.03.2016272.5 Кб142gister.docx
#
02.03.20162.15 Mб38glava04.pdf
#
02.03.2016863.36 Кб20glava05.pdf
#
02.03.2016325.23 Кб17glava1.pdf
#
02.03.2016445.13 Кб24glava5.pdf
#
02.03.2016717.37 Кб21glava6.pdf
#
02.03.2016603.71 Кб32glava7.pdf
#
02.03.20161.14 Mб15glava8.pdf
#
02.08.201999.33 Кб9Himia_reshenia_biletov.doc
#
08.11.2018860.16 Кб11Hist1.doc
#
09.11.201947.1 Кб5HOME READING ASSIGHNMENT.doc