glava6
.pdf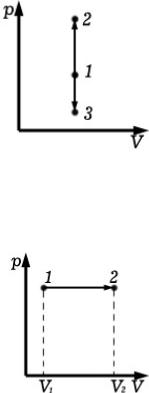
§ 33
Применение первого начала термодинамики к изопроцессам
1. Изохорный процесс ( V = const ). Диаграмма этого процесса (изохора) изображена на рисунке, где 1–2 есть изохорное нагревание, а 1–3 – изохорное охлаждение. При изохорном процессе газ не совершает работы, т.е.
δA = pdV = 0 .
Из I начала термодинамики ( δQ = dU + δA) для изохорного процесса следует
δQ = dU = |
|
m |
|
C |
|
|
dT. |
|
|
|
(33.1) |
|||||
|
M |
V |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Изобарный процесс ( p = const ). Диаграмма этого |
||||||||||||||||
процесса (изобара) изображена на рисунке. При |
изобарном |
|||||||||||||||
процессе работа газа при расширении объема от V1 |
до V2 рав- |
|||||||||||||||
на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A = ∫ pdV = p(V2 − V1 ) . |
|
(33.2) |
||||||||||||||
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из уравнения Клапейрона-Менделеева для двух состояний |
||||||||||||||||
pV = |
m |
RT и pV = |
m |
RT |
|
|||||||||||
|
|
|
|
|||||||||||||
1 |
|
M |
1 |
|
|
|
|
|
2 |
M |
2 |
|
||||
следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(V − V ) = |
m |
|
R |
(T − T ) . |
|
|
||||||||||
|
|
|
|
|||||||||||||
2 |
1 |
|
|
M p |
2 |
1 |
|
|
|
|||||||
Тогда выражение (33.2) для работы изобарного процесса имеет вид |
||||||||||||||||
A = |
m |
R(T − T ) . |
|
|
|
(33.3) |
||||||||||
|
|
|
|
|||||||||||||
|
M |
2 |
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В изобарном процессе из выражения (33.3) вытекает физический смысл
молярной газовой постоянной: R численно равно работе изобарного расшире-
ния 1 моля идеального газа при нагревании его на 1 К.
В изобарном процессе при сообщении газу массой m количества теплоты
δQ = m CpdT M
его внутренняя энергия возрастает на величину
dU = m CV dT . M
3. Изотермический процесс ( T = const ).
Диаграмма этого процесса (изотерма) изображена на
рисунке. Изотермический процесс описывается законом Бойля-Мариотта
pV = const. Согласно уравнения |
Клапейрона-Менделеева, в изотермическом |
||||||||||||||||
процессе работа равна |
|
|
|
|
|
|
|||||||||||
|
V2 |
|
V2 |
|
|
|
|
|
|
|
|||||||
A = |
pdV = |
m |
|
dV |
= |
m |
|
V2 |
|
= |
m |
|
p1 |
|
|||
∫ |
∫ |
RT |
RTln |
|
RTln |
. |
|||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
V1 |
|
V1 |
M V M |
V1 |
|
|
M |
p2 |
|
|||||||
Так как при T = const внутренняя энергия идеального газа не изменяется
dU = m CV dT = 0 , M
то из I начала термодинамики следует, что для изотермического процесса
δQ = δA ,
т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им ра-
боты против внешних сил
Q = A = |
m |
RTln |
p1 |
= |
m |
RTln |
V2 |
. |
(33.4) |
|
|
|
|
||||||
|
M |
|
p2 |
|
M |
|
V1 |
|
|
Следовательно, для того, чтобы при расширении газа внутренняя энергия не из-
менялась (T = const ), необходимо к газу подводить эквивалентное работе коли-
чество теплоты.
Задача 1. В баллоне емкостью 2 л находится углекислый газ под давлением
3 МПа при температуре 273 К. К газу подводят 18 кДж теплоты. Определите тем-
пературу и давление газа после нагревания.
Дано: |
СИ |
|
|
Решение |
V =1 л |
0,001 м3 |
Количество теплоты, полученное газом при |
||
i = 6 |
|
изохорном процессе, определим по формуле |
||
p1 = 3 МПа |
3×106 Па |
Q = CVν(T2 −T1 ) , |
||
T1 = 273 К |
|
где n – количество вещества, C – молярная тепло- |
||
|
|
|
|
V |
Q =18 кДж |
1,8×104 Дж |
емкость газа при постоянном объеме, которая опре- |
||
|
|
|
|
|
T2 = ? p2 = ? |
|
деляется выражением |
||
|
|
|
|
|
|
|
C = |
i |
R . Подставим это равенство в формулу |
|
|
|
||
|
|
V |
2 |
|
|
|
|
|
|
для количества теплоты
Q= i nR(T2 - T1) . 2
Запишем уравнение Клапейрона-Менделеева для начального и конечного
состояния газа
p1V = νRT1 и p2 V = νRT2 .
Из второго уравнения вычтем первое
(p2 −p1)V = νR(T2 −T1) .
С учетом этого равенства формула для количества теплоты примет вид
Q= i (p2 - p1)V . 2
Выразим отсюда конечное давление газа
p |
|
= |
|
|
2Q |
+ p . |
|
|
|||
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
iV |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Подставим числовые значения |
|
|
|||||||||
p2 |
= |
|
2 ×18000 Дж |
+ 3×106 |
Па = 6 ×106 |
Па = 6 МПа . |
|||||
|
|
|
|||||||||
|
|
|
|
|
|
6 ×0,002 м3 |
|
|
|||
Для определения температуры газа после нагревания запишем закон Шарля |
|||||||||||
|
p1 |
= |
p2 |
|
|
|
|
|
|||
|
T1 |
T2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
и выразим отсюда температуру во втором состоянии
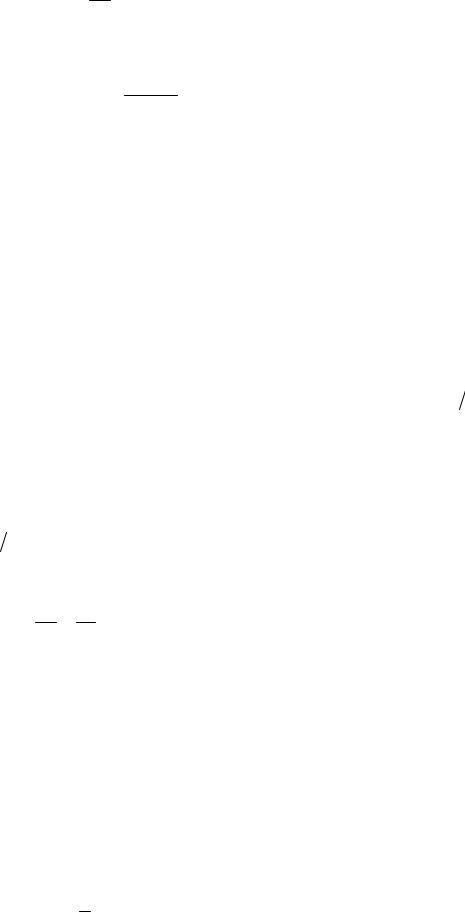
T2 = T1 p2 . p1
Подставим числовые значения
T2 = 273 К× 6 МПа = 546 К . 3 МПа
Задача 2. Двухатомный идеальный газ нагревают при постоянном давлении
150 кПа от температуры 200 К до температуры 400 К. Какую работу при этом со-
вершил газ, если его объем стал 20 л? Во сколько раз теплота, переданная газу,
больше изменения его внутренней энергии?
Дано: |
СИ |
|
|
|
|
|
Решение |
i = 5 |
|
Работа газа при изобарном процессе определяет- |
|||||
p = 150 кПа |
1,5×105 Па |
ся по формуле |
|
||||
T1 = 200 К |
|
|
A = p(V2 − V1 ) = pV2 (1− V1 V2 ) , |
||||
T2 = 400 К |
|
где V1 – |
начальный объем газа. Запишем закон Гей- |
||||
V2 = 20 л |
0,02 м3 |
Люссака |
|
|
|
|
|
|
|
|
V1 |
|
V2 |
|
|
A = ? |
|
|
= |
. |
|||
Q U = ? |
|
|
T1 |
T2 |
|||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выразим из него отношение объемов
V1 = T1
V2 T2
и подставим в формулу для работы газа
|
|
T1 |
|
|
|
- |
|
||
|
||||
A = pV2 1 |
T2 |
. |
||
|
|
|
В полученное равенство подставим числовые значения
|
|
|
200 К |
|
|
A = 1,5 ×105 |
Па×0,02 м3 × 1 |
- |
|
|
= 1500 Дж . |
|
|||||
|
|
|
400 К |
|
|
Изменение внутренней энергии газа определяется по формуле
DU = i nR(T2 - T1) , 2
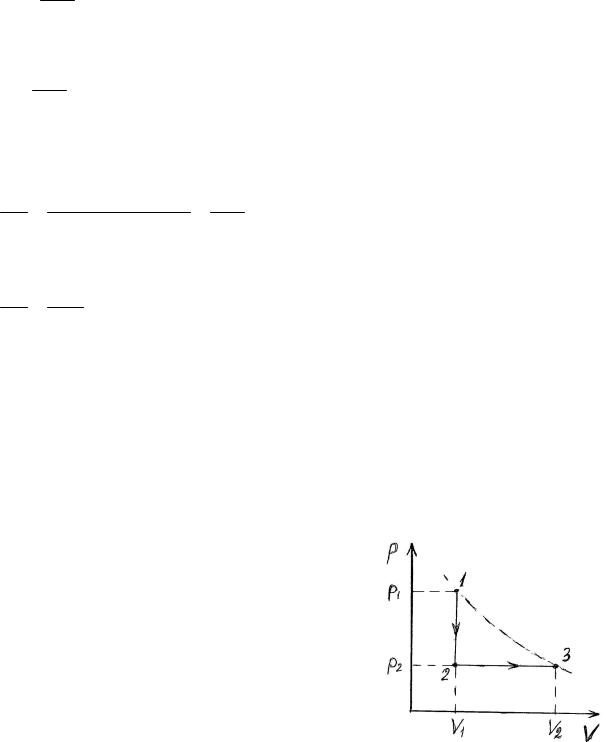
где ν – количество вещества, R – универсальная газовая постоянная. Количество теплоты, полученное газом в изобарном процессе, определяется выражением
Q = Cpν(T2 −T1) ,
где Cp – молярная теплоемкость газа при постоянном давлении, которая опреде-
ляется по формуле
Cp = i + 2 R . 2
Подставим это выражение в формулу для количества теплоты
Q = i + 2 Rν(T2 −T1 ) 2
и найдем отношение количества теплоты, полученной газом, к изменению его внутренней энергии в изобарном процессе
Q = 2(i + 2)νR(T2 −T1 ) = i + 2 . |
||
U |
2iνR(T2 −T1 ) |
i |
Подставим числовые значения
Q = 5 + 2 =1,4 .
U5
Задача 3. Три моля идеального газа при температуре 420 К охладит изохор-
но, вследствие чего его давление уменьшилось в 3 раза. Затем газ изобарно рас-
ширили так, что в конечном состоянии его температура стала равной первона-
чальной. Найдите полное количество теплоты, переданной газу в данных процес-
сах. |
|
|
|
|
|
||
|
|
|
|
|
|||
Дано: |
|
Решение |
|
|
|||
ν = 3 моля |
Количество |
теплоты, |
отданное |
||||
T1 = 420 К |
газом при изохорном охлаждении, |
||||||
|
p1 |
= 3 |
определяется формулой |
|
|
||
|
|
|
|
|
|
||
|
|
|
= C ν(T −T ) , где C |
– |
|||
|
p2 |
Q |
|||||
|
|
|
12 |
V |
2 1 |
V |
|
T1 = T3 |
молярная |
теплоемкость |
газа |
при |
|||
|
постоянном объеме, равная |
|
|
||||
Q = ? |
|
|
|||||
|
|
|
|
|
|
|
|
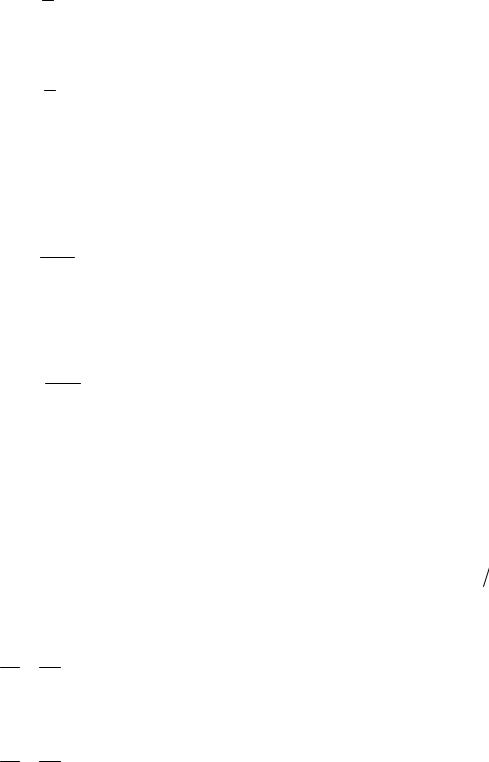
CV = i R . 2
Подставим выражение для молярной теплоемкости в формулу для теплоты
Q12 = i νR(T2 − T1 ) .
2
Количество теплоты, полученное газом при изобарном расширении, равно
Q23 = Cpν(T3 − T2 ) ,
где Cp – молярная теплоемкость газа при постоянном давлении, которая равна
Cp = i + 2 R . 2
Подставим выражение для молярной теплоемкости в формулу для количества те-
плоты и учтем, что T3 = T1
Q23 = i + 2 νR(T1 − T2 ) .
2
Полное количество теплоты, переданное газу в изображенных на рисунке процессах, равно
Q = Q12 + Q23 .
Подставим соответствующие выражения вместо Q12 и Q23 , тогда получим
Q = |
i |
νR(T − T ) + |
i + 2 |
νR(T − T ) = νR(T − T ) = νRT (1− T T ) . |
|||||||
|
|
||||||||||
2 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|||
Для изохорного процесса запишем закон Шарля
p1 = p2 . T1 T2
Выразим отношение температур
T2 = p2
T1 p1
и подставим в формулу для количества теплоты
Q = νRT |
|
− |
p |
2 |
|
1 |
|
. |
|||
|
|
||||
1 |
|
|
p1 |
|
|
|
|
|
|
||
Подставим числовые значения
|
|
1 |
|
|
|
|
Q = 3 моля×8,31 Дж/(моль× К) × 420 К× 1 |
- |
|
|
|
= 6980 Дж . |
|
3 |
||||||
|
|
|
|
|||
Задача 4. При изотермическом расширении 16 г кислорода, находящегося при 300 К, была совершена работа, равная 900 Дж. Во сколько раз изменилось
давление кислорода при расширении? |
|
|
|
|||||||||
Дано: |
|
СИ |
|
|
|
|
|
|
|
Решение |
||
|
|
|
|
|
|
|
|
|||||
T = const |
|
|
Работа газа при изотермическом процессе |
|||||||||
m =16 г |
|
0,016 кг |
определяется по формуле |
|||||||||
M = 0,032 кг/моль |
|
|
|
A = |
m |
RTln(p p |
|
) . |
||||
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|||||||
T = 300 К |
|
|
|
|
|
M |
1 |
|
||||
|
|
|
|
|
|
|
|
|||||
A = 900 Дж |
|
|
Выразим из этой формулы отношение давлений га- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 p2 = ? |
|
|
за в начале и конце изотермического процесса |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 |
|
|
|
AM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
= e |
mRT |
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
p2 |
|
|
|
|||||
Подставим в полученное равенство числовые значения
900 Дж×0,032 кг/моль
p1 = e0,016 кг×8,31 Дж/(моль×К)×300 К = 2 .
p2
Задача 5. Два моля идеального газа расширяется изотермически при темпе-
ратуре 150 К до объема втрое большего, чем первоначальный. Определите работу при расширении, изменение внутренней энергии газа и количество поглощенной
теплоты. |
|
|
|
|
|
Дано: |
|
Решение |
T = const |
Запишем первое начало термодинамики |
|
ν = 2 моля |
Q = A + DU . |
|
T =150 К |
При изотермическом процессе T = const и DU = 0 , тогда |
|
V2 V1 = 3 |
Q = A = νRTln(V |
V ) . |
|
2 |
1 |
|
|
|
A = ? Q = ? |
Подставим числовые значения |
|
DU = ? |
Q = A = 2 моля×8,31 Дж/(моль× К) ×150 К×ln 3 = 2740 Дж . |
|
|
|
|
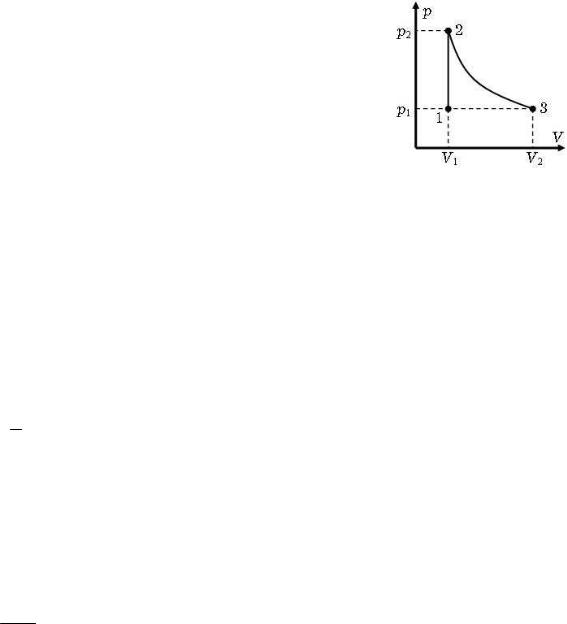
Задача 6. Два моля идеального одноатомного газа, занимавший объем 15 л
при давлении 150 кПа, нагревают до температуры 450 К при постоянном объеме,
а затем, изотермически расширяя, доводят его до первоначального давления. Най-
дите изменение внутренней энергии, работу и количество переданной газу тепло-
ты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дано: |
СИ |
|
|
|
|
|
Решение |
i = 3 |
|
Построим |
|
указанные |
|||
V =15 л |
0,015 м3 |
процессы изменения состояния |
|||||
1 |
|
|
|
|
|
|
|
p =150 кПа |
1,5×105 Па |
идеального |
газа |
на |
рисунке. |
||
1 |
|
|
|
|
|
|
|
ν = 2 моля |
|
Изменение внутренней энергии |
|||||
|
|
|
|
|
|
|
|
T2 = 450 К |
|
в этих процессах равно |
|||||
|
|
|
|
|
|
|
|
p1 = p3 |
|
U = |
U12 + |
U23 , |
|||
|
|
|
|
|
|
|
|
|
|
где U12 – |
изменение внутренней энергии в изохор- |
||||
U = ? |
|
||||||
|
|
|
|
|
|
|
|
A = ? Q = ? |
|
ном процессе, оно равно |
|||||
|
|
|
|
|
|
|
|
|
|
DU = |
i |
nR(T - T ) ; |
|||
|
|
||||||
|
|
|
|||||
|
|
12 |
2 |
|
2 |
1 |
|
|
|
|
|
|
|
||
изменение внутренней энергии в изотермическом процессе равно U23 = 0 . Тогда полное изменение внутренней энергии будет равно
DU = i nR(T2 - T1) . 2
Для определения температуры газа T1 в первом состоянии запишем уравнение Клапейрона-Менделеева для этого состояния
p1V1 = νRT1
и выразим из него температуру
T= p1V1 .
1nR
Сучетом этого выражение для изменения внутренней энергии имеет вид
DU = |
i |
nR T |
- |
p1V1 |
|
= |
i |
(nRT - p V ). |
|
|
|
||||||
|
2 2 |
|
nR |
2 |
2 1 1 |
|||
Подставим числовые значения
DU = 3 ×(2 моля×8,31 Дж/(моль× К) × 450 К -1,5 ×105 Па×0,015 м3 )= 7840 Дж. 2
Работа газа в указанных процессах равна
A = A12 + A23 ,
где A12 = 0 – работа газа в изохорном процессе, работа газа в изотермическом
процессе равна
A23 = νRT2 ln(p2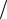 
p3 ) = νRT2 ln(p2 
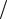p1 ) .
Тогда суммарная работа за указанные процессы будет равна
A = νRT2 ln(p2 
p1 ) .
Для определения отношения давлений запишем закон Шарля для изохорного про-
цесса и воспользуемся выражением для температуры T1
|
p1 |
= |
p2 |
, откуда |
p2 |
= |
T2 |
= νRT2 . |
||
|
|
|
|
|
||||||
|
T1 T2 |
|
p1 |
|
T1 |
p1V1 |
||||
Подставим эту формулу в выражение для работы |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nRT2 |
|
|
|
|
||
|
A = nRT2 ln |
p1V1 |
. |
|
||||||
|
|
|
|
|
|
|
|
|
||
Подставим числовые значения
|
2 моля×8,31 Дж/(моль× К) × 450 К |
|
||||
A = 2 моля×8,31 Дж/(моль× К) × 450 К×ln |
|
|
|
|
|
= |
|
5 |
|
3 |
|||
|
1,5 ×10 |
Па×0,015 м |
|
|
||
|
|
|
. |
|||
= 8980 Дж |
|
|
|
|
|
|
Для определения количества теплоты воспользуемся первым началом тер-
модинамики
Q = A + U .
Подставим числовые значения
Q = 8980 Дж + 7840 Дж =16820 Дж.
§ 34
Адиабатический процесс. Политропный процесс
Адиабатическим называется процесс, при котором отсутствует теплообмен ме-
жду системой и окружающей средой ( δQ = 0 ).
Из I начала термодинамики ( δQ = dU + δA) для адиабатического процесса следует, что
δA = −dU , |
(34.1) |
т.е. внешняя работа совершается за счет изменения внутренней энергии системы.
С учетом выражений для δA и dU для произвольной массы газа перепи-
шем уравнение (34.1) в виде
pdV = − |
m |
C |
|
|
dT . |
|
|
(34.2) |
||||
|
V |
|
|
|||||||||
|
|
M |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Продифференцировав уравнение состояния для идеального газа PV = (M M )RT , |
||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|||
pdV + Vdp = |
m |
RdT . |
|
(34.3) |
||||||||
|
|
|||||||||||
|
|
|
|
|
|
M |
|
|
|
|||
Исключим из (34.2) и (34.3) температуру T |
||||||||||||
|
pdV + Vdp |
= − |
|
R |
= − |
Cp − CV |
. |
|||||
|
pdV |
CV |
CV |
|||||||||
|
|
|
|
|
|
|
||||||
Разделив переменные и учитывая, что γ = Cp 
CV , получим
dp = −γ dV .
pV
Интегрируя это уравнение в пределах от p1 до p2 и соответственно от V1 до V2 , а
затем потенцируя, придем к выражению
p |
2 |
|
V |
|
γ |
|
= |
1 |
|
, |
|
|
|
|
|||
p1 |
|
V2 |
|
|
|
|
|
|
|||
или
p1V1γ = p2 V2γ .
Так как состояния 1 и 2 выбраны произвольно, то можно записать