Teoriya avtomatichnogo keruvannya

6.3

Основні шляхи підвищення точності керування. Замикання системи

Розглянемо найвщоміші напрями вирішення проблеми підвищення точності САР:

1) використання замкнутих САР і збільшення коефіцієнта підсилення регулятора (системи);

2)формування потрібних законів регулювання (введення астатизму регулювання за похідними);

3)використання спеціальних структур САР, які реалізують принципи керування, що забезпечують підвищення точності (комбіноване керування, системи зі змінною структурою);

4)реалізація принципів інваріантності;

5)використання різного виду коректувальних пристроїв.

Замикання САР і можливості підвищення точності. Як

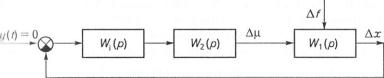
приклад розглянемо спрощену функціональну схему САР стабілізації (рис. 6.3), яка складається з об'єкта 1 і регулятора 2.

Рівняння замкнутої системи у відхиленнях має вигляд

[Р(Р)+0(Р)]АХ=<>(Р)РЛР)¥.

Нехай об'єкт — аперіодична ланка першого порядку, а регулятор — проста підсилювальна ланка. Тоді рівняння об'єкта і регулятора

( 7 > + \)х = £,/; \х = к2х.

При цьому Р(р) = (Т1р + 1); 0(р) = к{к2\ Р\ (р) = \ ;5(р) = к0 (де к0 — передаточний коефіцієнт об'єкта за збуренням).

Знайдемо помилки, які з'являються в розімкнутій і замкнутих системах. Запишемо рівняння розімкнутої системи в загальному вигляді

290

6.3. Основні шляхи підвищення точності керування. Замикання системи

А х -

( Т ї Р + 1 )

< миічна помилка цієї системи при і —» °о запишеться так:

Ах = Ахст = к() А/,

і) ро иГязок рівняння —

При замиканні системи її рівняння матиме вигляд

(7]/)+ 1 + /с1/с2)Ах = /с() А/,

ІІИДКИ

\/

Порівняння знайдених значень статичних помилок і розв'язків і'ішіяпь динаміки розімкнутої й замкнутої систем дозволяє зробити

іII І висновки.

І.Замикання САР дає змогу зменшити статичну помилку і сталу

ч.и-у в І + кЛк2 разів.

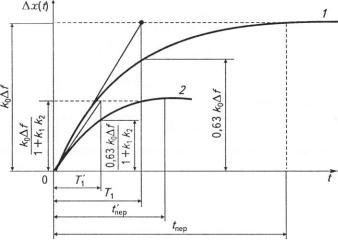
І. Графіки часових характеристик, наведених на рис. 6.4 (7 — ро- и и пу га; 2 — замкнута система), показують, що замикання системи ї м імогу зменшити також тривалість перехідного процесу в 1 + к}к2 ріі 1ІІІ.

ї\ збільшенням коефіцієнта підсилення регулятора к2 при за-

мш .ті і і системи можна зменшити її статичну помилку.

Замикання системи дозволяє також кардинально змінити динамічні властивості деяких об'єктів. Як вказувалося раніше, об'єкти з

291

Рис. 6.4

від'ємним коефіцієнтом самовирівнювання, які мають нестійкі часові характеристики, без регулятора є нездатними до роботи.

Рівняння такого об'єкта можна записати у вигляді

( 7 > - 1)Дхв1ІХ = к | А/.

Розв'язок його

Дх1вих = /С|Д/(е~'/г' - І ) - » ~

І - > оо

визначає нестійку роботу об'єкта без регулятора (в розімкнутій системі).

При введенні цього об'єкта в замкнуту систему з регулятором 2 (див. рис. 6.3), рівняння якого

(Т2р + \)[і = к2АхІШХ,

рівняння замкнутої системи матиме вигляд [ ( 7 > - 1 )(Т2р + 1) + /с,/с2 ]Ах1[ІИХ =^(р)Р1(р)А/,

292

6.4.Типові закони регулювання.

Введення астатизму і регулювання за похідними

Умови стійкості системи такі: Т{ > Т2 і > 1. Отже, нестійкий "•»>'< і і за певного настроювання замкнутої системи може забезпечиIII її стійку роботу.

6.4

Типові закони регулювання.

Введення астатизму і регулювання за похідними

Розглянуті вище приклади показують, що об'єкти в замкнутій системі набувають нових динамічних й

• і .і-гмчіїих властивостей і характеристик. Властивості замкнутих сис- п*м залежать не тільки від характеристик об'єкта і діючих збурень, а п під особливостей і характеристик регуляторів.

Регулятори поділяють за різними ознаками:

•за видом енергії, що використовується, — пневматичні, механічні, гідравлічні, електричні;

•за принципом керування — керування за відхиленням (помилкою), за збуренням, комбіновані;

•за характером передачі сигналів — неперервні, дискретні;

•за характером зв'язків між елементами системи — зі сталою та змінною структурами.

УТАК однією з основних особливостей регулятора є можливість ми шву на статичні й динамічні помилки САР, що залежить від характеристик регулятора, які визначаються його законом керування (регулювання).

11 ід законом регулювання розуміють залежність вихідної величини ргі улятора \і від його вхідної величини х за умови, що інерція самого Р< іулятора не враховується (див. рис. 6.3):

ц = Дх).

Залежно від вигляду функції Дх) існують три основні принципо- ш закони та відповідні їм типи регуляторів: пропорційний, який реашусться за допомогою пропорційного регулятора (ГІ-регулятора);

інтегральний (І-регулятора); диференціальний (Д-регулятора).

293

На практиці здебільшого використовують комбіновані закони регулювання, які об'єднують позитивні властивості вказаних вище принципів керування і відповідних регуляторів.

Розглянемо основні властивості і особливості названих регуляторів.

Пропорційний закон регулювання (П-регулятор). Це

найпростіший закон керування. Він описується залежністю

Властивості П-регулятора і характер його дії вже розглядалися при дослідженні впливу замикання системи на її статичну помилку та часові характеристики.

До п е р е в а г П-регуляторів належать: простота і надійність, безінерційність, можливість зменшення статичної помилки і тривалості

впливу на динамічні похибки і неможливість повної ліквідації статичної помилки. Останнє визначається тим, що при різкому збільшенні коефіцієнта передачі розімкнутої системи, яке необхідно для відповідного зменшення статичної помилки, система може стати нестійкою (для зменшення статичної помилки до нуля коефіцієнт передачі має дорівнювати нескінченності).

Інтегральний закон регулювання (І-регуляторА Інтег -

ральний регулятор виконує регулювання за інтегральним законом

Інтегрування вихідної величини об'єкта Ах в інтегральному регуляторі виконується за допомогою серводвигуна, що відповідає введенню в структурну схему САР інтегрувальної ланки (рис. 6.5) з передаточною функцією

Ах р

294

6.4.Типові закони регулювання.

Введення астатизму і регулювання за похідними

Рис. 6.5

Нехай передаточна функція замкнутої системи за збуренням до ши'дсчшя інтегрувальної ланки має вигляд

А/ 1 + Щ р У

пII (р) = \У{ (р)\У2(р) — передаточна функція розімкнутої системи;

II/ (р) передаточна функція об'єкта за збуренням.

ІІри цьому статична помилка

1 + ІУ(р) Р = о

і . истема буде статичною.

Після введення інтегрувальної ланки передаточна функція роимкнутої системи

Щр) = Щ (р) (р) ^ (Р) = Щр)к - ,

і і і а пічна помилка

Р/ 7 = 0

Ііітут11ість статичної помилки свідчить про те, що система після мін'дення інтегрувальної ланки зі статичної перетворилася на аста1114! іу.

І Іри цьому треба мати на увазі, що інтегрувальну ланку (ланки) « мц вводити в структурну схему так, як показано на рис. 6.5, — на

295

вхід об'єкта, точніше, до точки прикладання збурення, яке діє на об'єкт. Якщо інтегрувальну ланку ввести в САР після точки прикладання збурення (рис. 6.6), то, розглядаючи систему стабілізації [у(ї) = = 0], дістанемо передаточну функцію за збуренням з урахуванням

введення інтегрувальної ланки з передаточною функцією И/1 (р) = к —,

Р

яка матиме вигляд

Рис. 6.6

Статичну помилку знайдемо за формулою

о с к і л ь к и ІУ{ (0) Ф 0; І У 2 ( 0 ) Ф 0 .

Нерівність нулю Дхст свідчить про неможливість ліквідувати статичну помилку в разі неправильного введення інтегрувальної ланки між точкою прикладання збурення й об'єктом.

Введення інтегрувальної ланки задля ліквідації статичної помилки і перетворення статичної системи на астатичну називають

введенням астатизму в с и с т е м у .

За однієї інтегрувальної ланки кажуть про введення астатизму першого порядку, за двох — астатизму другого порядку і т. д. Введення астатизму другого і вищих порядків дає змогу ліквідувати динамічні (швидкісні) помилки, які виникають у системі в разі зміни зовнішніх збурень.

296

6.4.Типові закони регулювання.

Введення астатизму і регулювання за похідними

- оплюють прямим зв'язком (рис. 6.7). Таку нову ланку називають

і икїромною інтегрувальною.

Рівняння ізодромної ланки

Лх'ІЛ ІУ — ЛXОУ 41- X1) І IV •

Оскільки рівняння вихідної інтегрувальної ланки хвих = к — хах,

Р

і1 > шіхіднии сигнал

297

дромною. У цьому разі вигляд характеристичного рівняння замкнутої системи відповідатиме структурно-стійкій системі:

Отже, заміна інтегрувальної ланки ізодромною дає змогу струк- турно-нестійку систему перетворити на структурно-стійку.

Проаналізуємо вплив введення астатизму першого і другого порядків у САР за допомогою методу коефіцієнтів помилок.

Розглянемо слідку вальну систему з об'єктом у вигляді аперіодич-

і безінерційним регулятором з передаточною функцією \У2(р) = к2.

Передаточна функція замкнутої системи за помилкою матиме вигляд

Знайдемо коефіцієнти помилок. Розкладаючи передаточну функцію в ряд, розділимо чисельник на знаменник:

298

6.4.Типові закони регулювання.

Введення астатизму і регулювання за похідними

РТхр+ 1 р

їм.підемо коефіцієнти помилок:

Ч У

,І І.ІКОЖ передаточну функцію після розкладання в ряд у загальному піп пиді

<) гже, як зазначалося раніше, після введення в систему однієї ініеірувальної ланки (астатизму першого порядку) статична система перетворилася на астатичну (С0 = 0). При цьому в системі залишили- < н помилки за швидкістю (Сх Ф 0) і прискоренню (С2 Ф 0). Для усу- н е н н я швидкісної помилки необхідно ввести в систему астатизм другого порядку. Тоді при двох інтегрувальних ланках передаточна функція

299