4.3 Аналіз моделі множинної регресії

Як видно з отриманого рівняння моделі, вплив оборотних кошті на валовий доход майже в 10 разів більший, ніж обсяг основних фондів, що відображає реалії ринку: «живі гроші дають більший і швидкий доход чим вкладання в розвиток виробництва. Однак не слід забувати, що порівняння можливе лише при однаковій розмірності незалежних змінних (наприклад х₁ і х₂ виражені в тис. гривень, але не в тисячах і мільйонах гривень). Так само не можна порівнювати ці впливи при різному фізичному змісті змінних. Наприклад, якщо х₁ - інтенсивність руху (авт/год.), а х₂ - ширина проїзної частини (м), то співвідношення коефіцієнтів а₁ і а₂ взагалі не може служити мірою порівняння ступеня впливу цих параметрів на у - пропускну здатність автомобільної дороги.

Однак, щоб зробити можливим порівняння коефіцієнтів регресії й оцінити відносний вплив змінних х_j на у відносних одиницях, застосовують нормування коефіцієнтів регресії (а_j).

Коефіцієнт а_j показує величину зміни в значеннях СКО величини у зміні на одне СКО величини х_j тобто

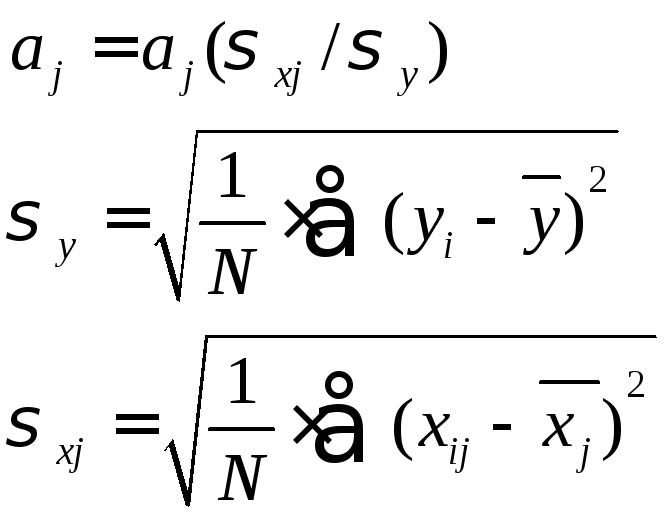
Зокрема, для розглянутого прикладу

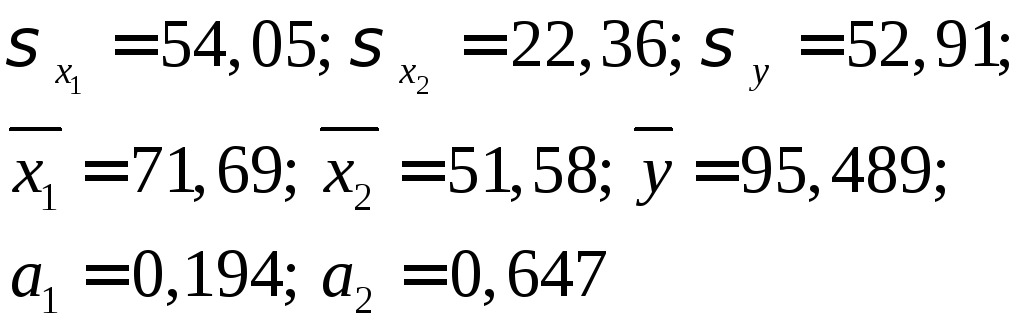
У такий спосіб відносний вплив х₂ на виявився більшим лише в

Для статистичної оцінки тісноти зв'язку застосовуються, як і в рівняннях парної регресії, ті ж самі три показники варіацій і коефіцієнти тісноти зв'язку, що базуються на них.

Основні показники варіації:

1) Загальна дисперсія, що відображає сукупні впливи всіх об'єктивно діючих факторів:

2) Факторна дисперсія, що відображає вплив тільки вивчених незалежних змінних.

де - значення, розраховані по моделі, для кожногоі-го зі сполучень х_j (j є т ), що мають місце в даному експерименті.

3) Залишкова дисперсія, що відображає вплив неврахованих змінних (крім х_j (j= ));

У цій формулі вираз в дужках показує відхилень експериментальних даних відносно рівняння регресії. Для розглянутого випадку маємо

З огляду на те, що одержимо вираження для залишкової дисперсії

По величині , зокрема, можна оцінювати точність різних моделей регресії.

Відношення

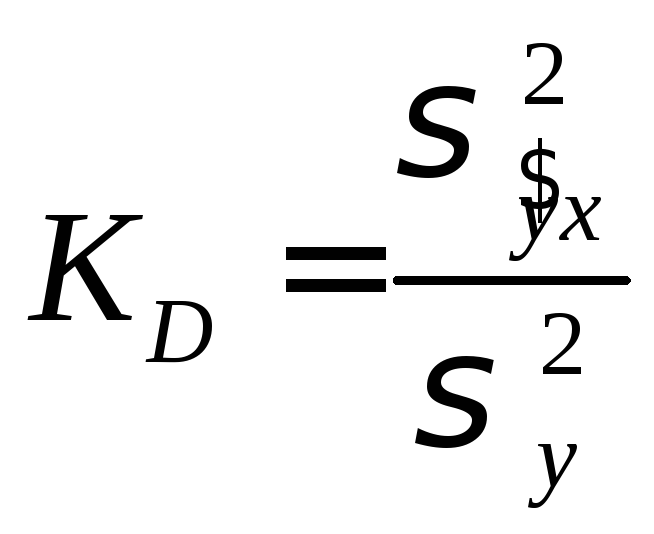
у даному випадку є коефіцієнтом множинної детермінації (для нелінійної регресії - індекс детермінації) і характеризує ступінь впливу обраних незалежних змінних на результативну ознаку у

Для розглянутого прикладу

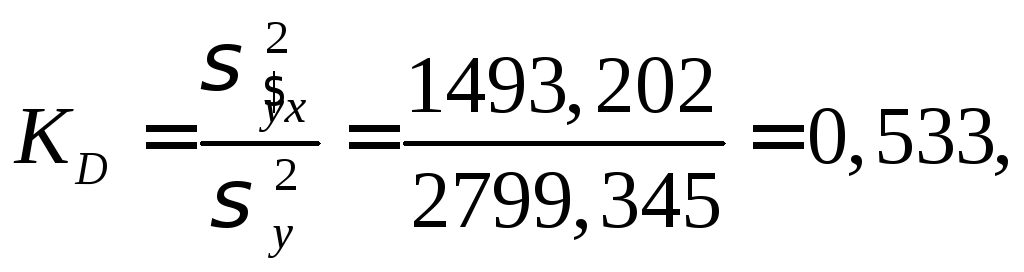
тобто 53,3% мінливості у обумовлені саме мінливістю х₁ і х₂.

Тоді коефіцієнт множинної кореляції ( для нелінійної регресії індекс кореляції) визначається як

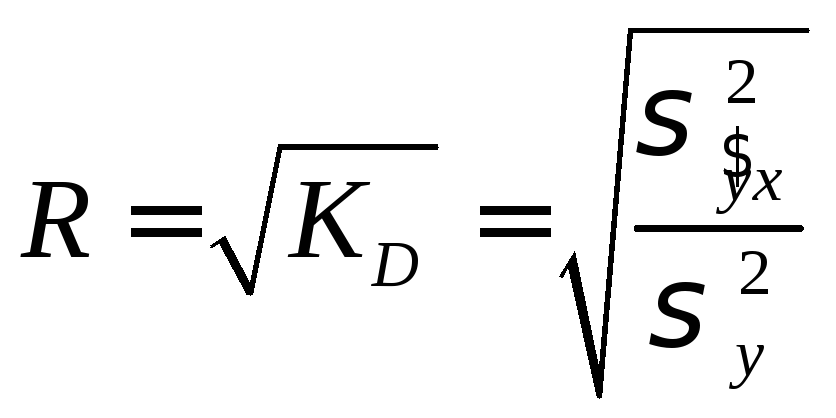
Для розглянутого приклада R=0,73, що свідчить про досить значний взаємозв'язок між y та х₁ і x₂

З огляду на те, що можна одержати трохи зручнішу для практичних розрахунків формулу, яка широко використовується при розрахунках моделей із застосуванням ЕОМ.

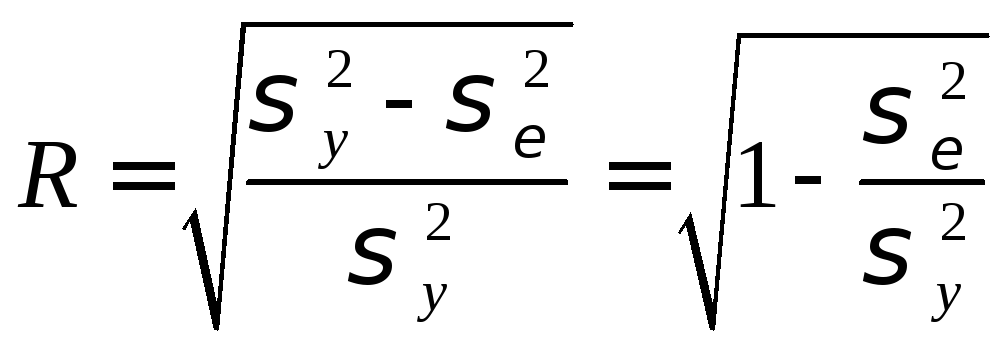
Неважко показати, що при m=l (тобто при парній регресії у(х)), це вираження збігається з раніше отриманим вираженням коефіцієнта R для лінійної регресії.

Завершуючи розгляд множинної регресії, приведемо ще одну корисну формулу для розрахунку величини R у матричній формі, що буде використовуватись при розрахунках значення R на ЕОМ: