2.2.2. Вибір форми функціональної залежності

Для визначення форми функціональної залежності будується кореляційне поле y(х_j) для кожної із змінних, що досліджуються. Для цього на осях координат у і х наносяться пари експериментальна отриманих значень y_i та х_i

(і =) (див. рис.2.2).

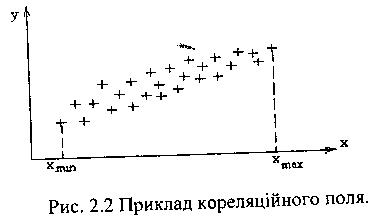
На кореляційному полі знаходяться x_min та х_mах - мінімальні та максимальні значення незалежної змінної х (саме це і є область, для якої визначаються параметри статистичної моделі).

По характеру розподілення точок кореляційного поля обираються форми функціональної залежності.

Найбільш простим і наочним являється метод інтервального усереднення. Для цього весь інтервал (від x_min до х_mах) розбивається на ряд ділянок (зазвичай не більше 7—10 ділянок) в кожному з яких знаходиться середнє значення змінної у:

Рис 2.3 Інтервальне усереднення даних кореляційного поля

де n_j- число значень у_ij ,що потрапили в j-й інтервал х_i (j = ; n =5...10).

Отриманні значення співвідносять з серединоюj-го інтервалу х_j (2.3) і отримані точки з'єднують ламаною чи плавною кривою. По характеру отриманої кривої і визначають форму функціональної залежності у(х).

Найбільш проста і найбільш часто вживана є лінійна модель виду:

(2.5)

що є зображеною на рис.2.4

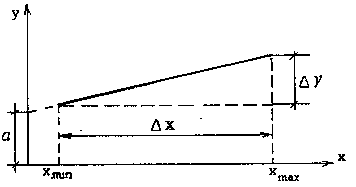
Рис.2.4 Графічне тлумачення лінійної моделі

При цьому потрібно пам'ятати, що отримані точки у, не обов'язково повинні розташовуватися на цій залежності, але їх розсіювання відносно даної прямої повинне бути мінімальним.

Серед нелінійних моделей часто використовують наступні моделі:

1) Див.рис.2.4а:

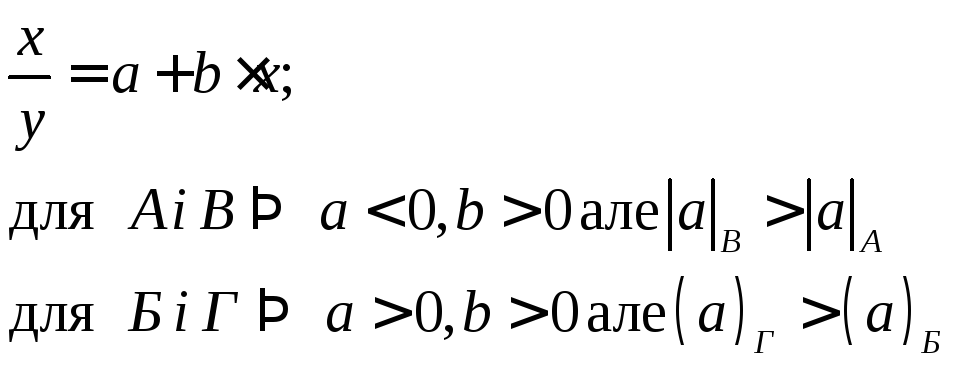(2.6)

Рис. 2.4а

2)Див.рис.2.4б:

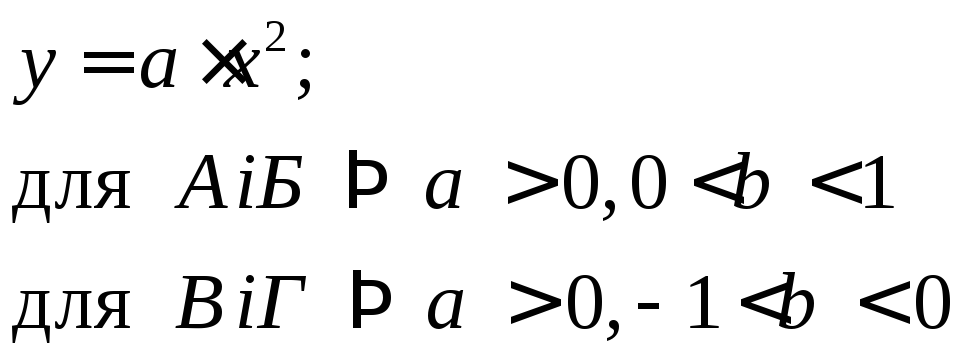(2.7)

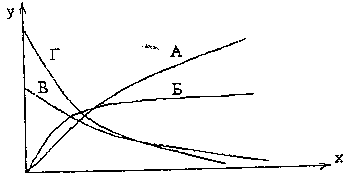
Рис. 2.4б

3)Див.рис.2.4в

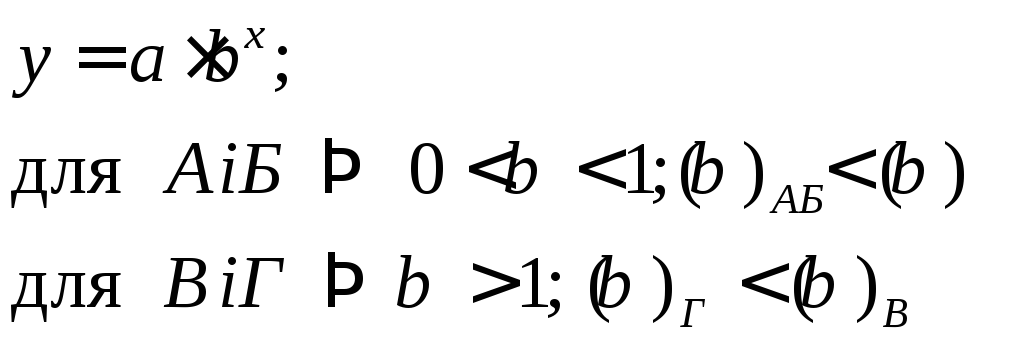(2.8)

Рис.2.4в

Після вибору форми функціональної залежності проводять лінеаризацію нелінійної моделі (тобто її штучне зведення до лінійної форми)

Наприклад:

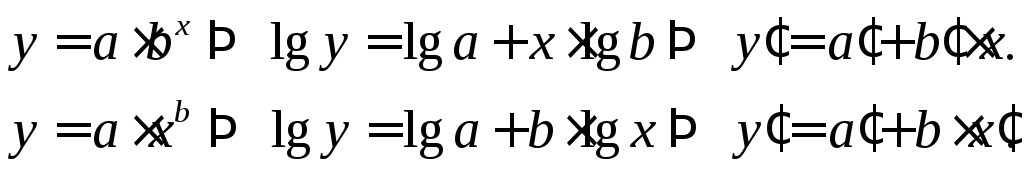
і т.п.

Часто зручним виявляється використання вихідної таблиці 2.1 експериментальних даних, кодовану по х (за х приймається номер рівномірного інтервалу).

Таблиця 2.1

x	y	Δy	Δ2y	lny	Δlny	x/y	Δx/ Δy
1	62,1	-	-	1,79246	-	0,01610	-
2	87,2	25,1	-	1,93962	-0,14716	0,02293	0,0683
3	109,5	22,3	-2,8	2,03941	0,09979	0,027,9	0,00446
4	127,3	17,8	-4,5	2,10483	0,06542	0,03142	0,00403
5	134,7	7,4	-10,4	2,12937	0,02454	0,03712	0,00570
6	136,2	1,5	-5,9	2,13386	0,00449	0,04405	0,00693
7	134,9	-1,3	-2,8	2,13001	-0,00383	0,05189	0,00784

Розрахуємо різниці, приведені у даній таблиці. Потім оцінимо можливість застосування різних моделей:

у = а + bx.

Ця модель незадовільна, оскільки відношення = Δy не є постійним.

у = аb^х

Ця модель приводиться до виду:

Ця модель також незадовільна, оскільки непостійне.

Ця парабола незадовільна, оскільки непостійне.

Оскільки відношення постійне (при Δх = 1), то цю модель можна використовувати для апроксимації експериментальних даних.

Поліноміальна модель

V випадку, коли вищерозглянуті моделі не дозволяють знайти задовільну апроксимацію експериментальних даних, часто використовується поліноміальна апроксимація виду:

(2.9)

В залежності від значень а_i (і =) можливо підібрати досить гарну відповідність моделі і експериментальним даним.

Лінеаризацію моделі даного типу проводять шляхом вводу нових змінних: х₁=х; х₂=х²; х₃=х³; ... х_k=x^k. Тоді поліноміальна модель прийме вид лінійної моделі з k-змінними:

(2.10)

Такого виду лінійні моделі носять назву моделей множини лінійної регресії. Далі, при вивченні моделей множинної лінійної регресії ми розглянемо алгоритм пошуку числових значень коефіцієнтів a_і (i=) що забезпечують мінімальне розсіювання експериментальних даних y_i відносно значень у отриманих за допомогою моделі множинної лінійної регресії у(х_і) і =.

Завертаючи розгляд вибору форми функціональної залежно-відмітимо, що в практиці велика кількість моделей зводиться або лінійної парної регресії у=а₀+bх, або до множинної лінійної регресії . Тому далі ми розглянемо саме ці моделі.