10.1.1. Принцип управління по збуренню

Основна ідея цього методу полягає не стільки в корегуванні стану об'єкту, що знаходиться під впливом багатьох збурень, а в компенсації саме їх впливу на об'єкт. Це дозволяє певним чином "захистити" об'єкт від впливу зазначених збурень.

Загальна структурна схема системи управління, що реалізує принцип управління по збуренню, представлена на рис. 10.2.

Рис. 10.2. Узагальнена реалізація принципу управління по збуренню

На рис.10.2. означені:

k_λ - коефіцієнт передачі елемента зв'язку по обуренню;

k_р - коефіцієнт передачі регулюючого елемента (регулятора);

- порівняльний пристрій (компаратор), що порівнює, у загальному випадку, дві будь-які величини (в даному випадку це ψ - деяке задане значення збурення, для якого розраховані параметри системи, та λ_И - вимірюване значення реального збурення). Значення Ψ- у техніці часто називають завданням системи управління, або вставкою.

- вихідний сигнал компаратору, який характеризує невідповідність реального значення λ_И заданому значенню Ψ. В техніці цей сигнал часто називають сигналом непогодження.

Приймемо, для простоти, що ОУ описується лінійною моделлю. Методика отримання подібних моделей нами розглядалась раніше, в попередніх розділах.

Для подібної моделі з двома вхідними змінними та однією вихідною можна записати:

Для решти елементів схеми запишемо наступні співвідношення:

З урахуванням вищезазначених рівнянь отримаємо залежність між вихідною змінною системи ψ та вхідними змінними λ та Ψ:

Нехай стан системи характеризується певними значеннями φ₁;μ₁; λ₁. Для варіацій φ відносно φ₁ можна записати:

Для спрощення записів ми замінили варіації Δφ на φ (аналогічно для Δλ і Δμ). Цей запис ми збережемо і в наступному.

З огляду на те, що , можна записати:

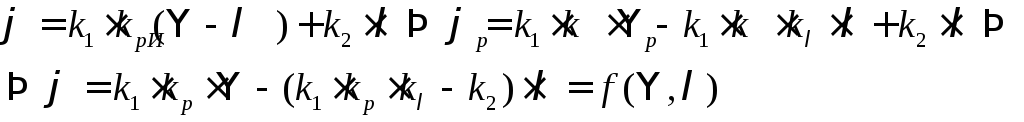
Щоб забезпечити незалежність φ від λ, необхідно виконати умову:

тобто .

Таким чином, знаючи коефіцієнти впливу λ і μ на значення φ (тобто величини k₁ і k₂ а також знаючи коефіцієнт перетворення λ -> λ_И (зазвичай приймають k_λ =1, якщо інформація про реальне значення λ потрапляє в систему без викривлень) можна визначити коефіцієнт регулятора k_р, який забезпечить незалежність φ від λ за допомогою простої формули:

(10.1)

Слід зазначити, що лінійні моделі використовуються, як правило, для незначних варіацій змінних і з їх допомогою можна оцінювати лише варіації змінних відносно їх планових (заданих) значень.

10.1.2. Принцип управління по відхиленню (принцип зворотного зв'язку)

Цей принцип, реалізований спочатку майже одночасно в регуляторах рівня (запропоновано вперше відомим російським інженером І. Ползуновим) і в регуляторах швидкості обертів двигуна (запропоновано вперше англійським вченим Д. Уаттом), у подальшому був узагальнений американським вченим Н.Вінером як фундаментальний принцип побудови будь-яких систем (як технічних, так і організаційних та економічних).

Якщо принципи управління по збуренню характеризуються відсутністю прямого безпосереднього зв'язку між φ і μ, у відповідності з принципом управління по відхиленню зв'язок між (φ і μ повинен обов'язково мати місце.

З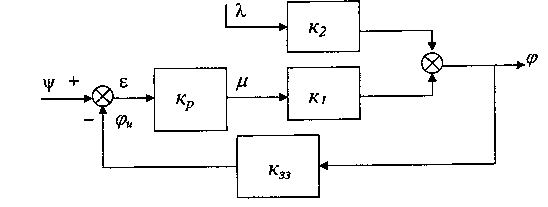агальна структура системи, що реалізує даний принцип управління зображена на рис. 10.3.

Рис. 10.3. Узагальнена реалізація принципу управління по відхиленню

де: - символ алгебраїчного додавання;

к₃₃- коефіцієнт зворотного зв'язку, що дозволяє вибирати μ з урахуванням реального значення φ.

Приймемо ту ж лінійну модель ОУ:

Оскільки сигнал зворотнього зв'язку віднімається від Ψ, тому подібний зворотній зв'язок має назву від'ємного зворотного зв'язку і є дуже поширеним елементом систем управління.

Враховуючи:

одержуємо:

(10.2)

Як випливає з цієї формули, при збільшенні значення k_р вплив λ на φ зменшується, але неможливо домогтися повної компенсації цього впливу, як у системі із застосуванням принципу управління по збуренню.

Відзначимо, що як у першому, так і в другому випадку φ визначається величиною завдання ψ, тобто заданим значенням.

Щоб глибше зрозуміти роль регулятора k_р розглянемо відхилення системи .

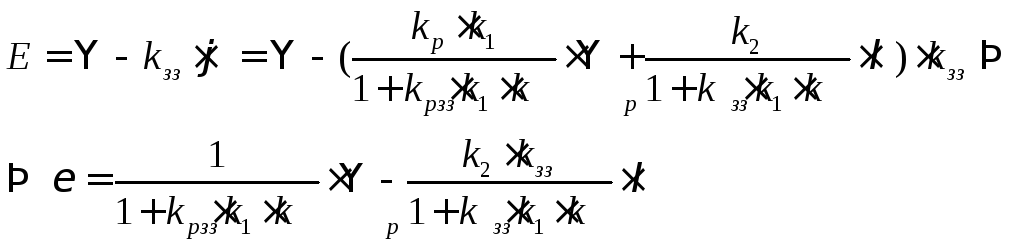(10.3)

Очевидно, що при .

Відмітимо дуже важливий випадок систем з одиничним зворотнім зв'язком, тобто при k₃₃=1. В цьому випадку φ=Ψ, тобто змінна, що підлягає управлінню, в системах з одиничним зворотнім зв'язком завжди дорівнює заданому значенню ψ і при його зміні має властивість їй слідувати.

На відміну від раніше розглянутої системи управління по обуренню, для системи управління по відхиленню немає необхідності вводити інформацію про збурення. Впливи кожного з них в системах зі зворотнім зв'язком послабляються в раз.

Дійсно, додавши в схему рис. 10.3 додаткове обурення λ і застосувавши відповідно модель виду

одержимо:

де: - коефіцієнт передачі системи в розімкнутому стані.

Остаточно матимемо:

(10.4)

Щоб визначити k₀ , досить умовно відключити зворотній зв'язок у місці його прикладання і перемножити значення усіх послідовно з'єднаних коефіцієнтів, що входять у замкнений зворотнім зв'язком контур управління.

З формули (10.4) слідує, що точність будь-якої системи зі зворотним зв'язком підвищується, якщо збільшити коефіцієнт передачі системи в розімкненому стані (за рахунок підвищення абсолютної величини k_р).