4.1 Матрична форма моделі множинної регресії
В практиці розрахунків коефіцієнтів множинної регресії часто використовується матрична форма запису рівняння регресії.
В цьому випадку для уніфікації запису рівняння регресії у перши доданок формули (4.5) уведемо штучну змінну x0=1=const.
При
оцінці параметрів цього рівняння в
кожному і-му
спостереженні фіксують значення уі
і
хji
(
).
Значене результативної змінноїу,
розрахованої по моделі (4.5), позначимо
через
.
Тоді похибка моделі ві-му
спостереженні буде дорівнювати
з математичним сподіванням, рівним 0 і
дисперсією
,
як це було показано вище.
Рівняння регресії між векторами значень Y і незалежних змінних Х записуємо в матричній формі як
де
Х={хij}
-
матриця значень незалежних факторів
(змінних) розмірності (
(нагадаємо, що хі0
=1
(і=
);
-
вектор стовпець оцінок уі
розмірністю (
);
- вектор
невідомих параметрів моделі, розмірністю
(
)
(нагадаємо, що мається також вільний
член а0).
При
прийнятих позначках вектор експериментальних
значень Y
розмірністю
(
)
може бути представлений у виді
(4.12)
де E={εi}
вектор помилок моделі розмірністю (
).
Очевидно (див. 4.12), що
E=Y-XA
Нагадаємо деякі властивості матриць:
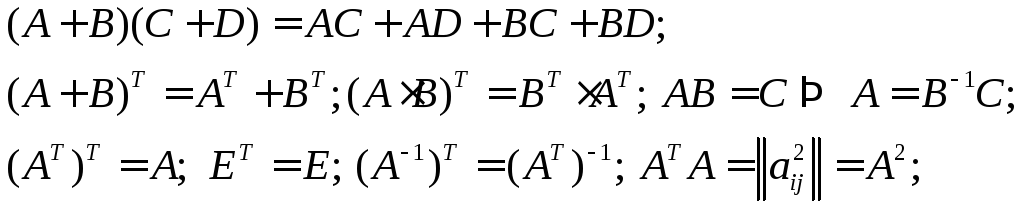
де
-
зворотна матриця,
- визначник матриці А;
- алгебраїчне доповнення до мінору
.
З використанням зазначених властивостей матриць запишемо суму квадратів відхилень:
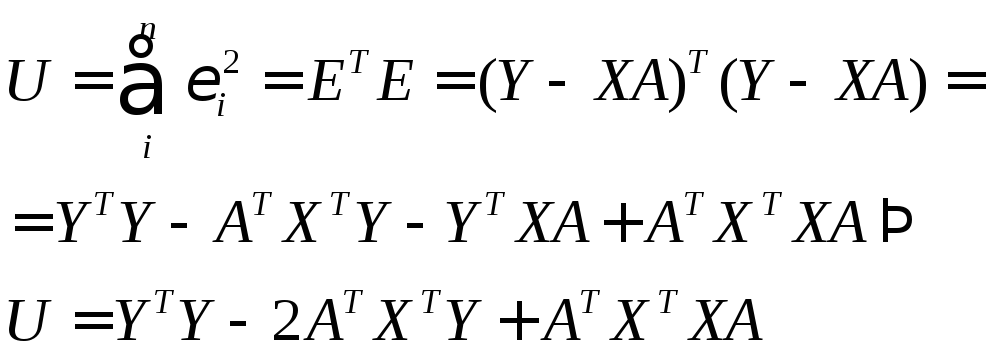
Диференціюючи по А, і прирівнюючи отриману похідну до нуля, одержуємо:
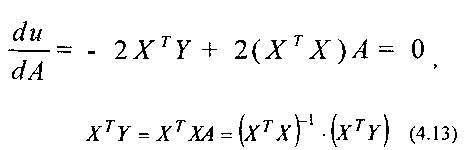(4.13)
Таким чином, матриця параметрів моделі рівняння множинної регресії, що забезпечують мінімум СКО, може бути отримана безпосередньо з експериментальних даних.
Конкретизуємо величини, що входять до формули (4.13):
тобто кожен рядок являє собою вибірку т незалежних змінних, крім x0=l=const.
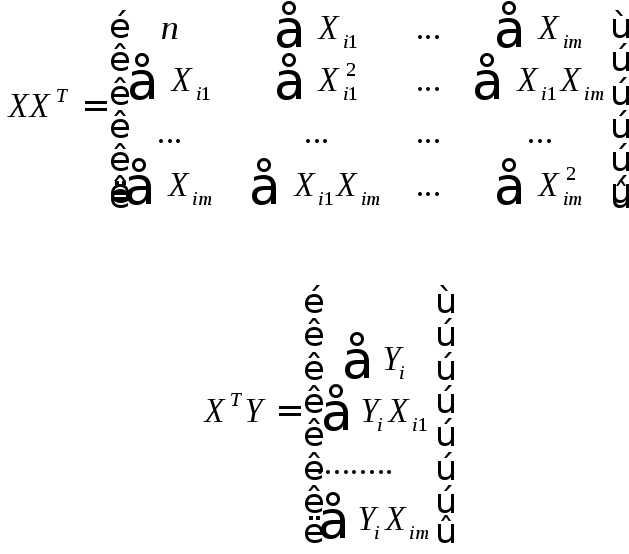
Підсумовування кожного елемента зазначеного в матриці здійснюється по кількості спостережень N.
4.2 Приклад побудови рівняння множинної регресії
Нехай досліджується залежність валового доходу від різних факторів. Приймемо гіпотезу про те, що валовий доход (у) залежить від обсягу основних фондів (х1,) і величини обсягу оборотних коштів (х2). При цих припущеннях визначимо коефіцієнти моделі множинної регресії виду
і оцінімо
якість отриманої моделі. Для цього
використаємо експериментальні дані
значень
,
які отримані по 19 магазинах аналогічного
профілю (див. таблицю 4.2) Отже, згідно
таблиці 4.2:
Табл.4.2 Дані експериментальних обстежень 19 магазинів
|
| ||||
|
Номер магазина____ |
уі |
µ |
х1і |
х2і |
|
1 „___ |
203,4 |
186,95 |
119,0 |
105,4 |
|
2 |
63,3 |
93,95 |
28,1 |
56,0 |
|
3 |
36,1 |
59,45 |
15,9 |
35,0 |
|
4 |
34,4 |
66,19 |
36,8 |
36,8 |
|
5 |
45,9 |
89,18 |
17,5 |
54,2 |
|
6 |
113,7 |
109,52 |
50,3 |
63,4 |
|
7 |
121,8 |
54,5 |
55,9 |
26,8 |
|
8 |
70,8 |
73,96 |
26,1 |
43,2 |
|
9 |
87,8 |
69,27 |
21,6 |
40,7 |
|
10 |
75,8 |
109,53 |
25,4 |
66,5 |
|
11 |
49,0 |
44,53 |
17,2 |
25,10 |
|
12 |
111,8 |
108,76 |
119,6 |
54,3 |
|
13 |
96,4 |
90,635 |
124,2 |
41,9 |
|
14 |
80,0 |
80,11 |
114,8 |
36,2 |
|
15 |
88,9 |
111,1 |
166,5 |
50,0 |
|
16 |
75,2 |
111,98 |
109,5 |
58,4 |
|
17 |
61,8 |
95,23 |
141,1 |
42,8 |
|
18 |
237,7 |
195,64 |
154,2 |
106,7 |
|
19 |
160,5 |
63,83 |
24,4 |
36,8 |
|
Разом |
|
|
|
|
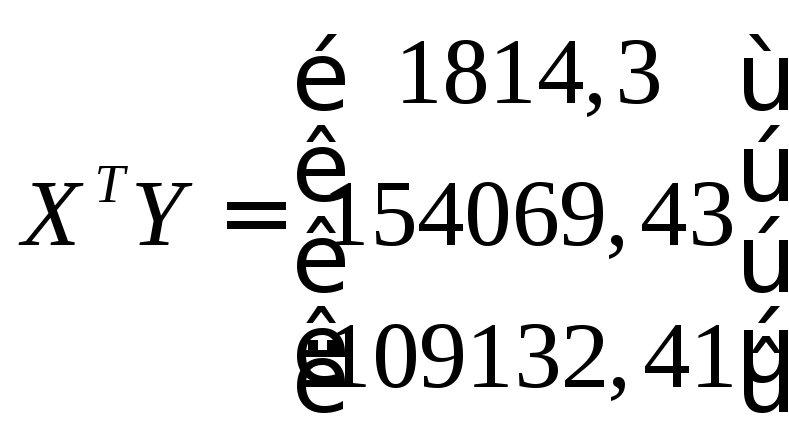
зворотна матриця (ХTX)-1 має вид:
Вектор коефіцієнтів дорівнює:
Отже:
тоді рівняння регресії набуде виду:
