7 Вопрос.

Система линейных уравнений:

Определители:

Решение:

Пример:

Определители:

8 Вопрос.

Покажем, как методом Гаусса можно решить следующую систему:

Обнулим коэффициенты при во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на и , соответственно:

Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на :

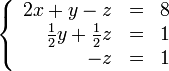
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

 из третьего;

 из второго, подставив полученное 

 из первого, подставив полученные и .

Таким образом исходная система решена.

В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.

9-11 вопросы.

1. Основные формулы в декартовых прямоугольных координатах

     При решении задач аналитической геометрии будем использовать действия над векторами, заданными в координатной форме.      Пусть даны векторы и. Тогда:      1) при сложении (вычитании) векторовполучим вектор;      2) при умножении векторана число λ получим вектор;      3) при скалярном произведении векторовполучим число.Расстояние между двумя точкамиДаны точкиА(x_A,y_A) и В (x_В, y_В). Расстояние между ними найдем, как длину вектора= (x_В–x_А,y_B -y_A). Из скалярного произведенияимеем. Подсчитав скалярное произведение через координаты вектора, получаем расстояние между двумя точками.                                  (1)Угол между двумя векторамиДаны два вектора:и. Косинус угла между ними:.                            (2)Деление отрезка в заданном отношенииПусть даны точки А (x_Аy _А), и В (x_Вy _В). Требуется найти координаты точки С (x,y) , делящей отрезок  АВ в заданном отношении λ:

В      A                           С

.

     Для решения задачи воспользуемся действием умножения вектора на число. Перепишем отношение  в виде: |AC|=λ| CB|. Такое соотношение длин может быть получено при выполнении действия.      В равных векторах равны соответствующие координаты:.      Из этих уравнений найдем неизвестные координаты точки С:.                                    (3)      В частности, для середины имееми поэтому λ=1. Следовательно, координаты середины отрезка находятся по формулам:(4)Условия параллельности и перпендикулярности векторовТак как скалярное произведение двух перпендикулярных векторовиравно 0, то условием перпендикулярности отличных от нуля векторов будет равенство.      При умножении векторана скалярполучаем вектородного направления спри λ > 0и противоположного направления при λ < 0. Но всегда векторыбудут параллельны.      Поэтому условием параллельности векторовбудет пропорциональность их соответствующих координат:.      Пример. Найти длину медианыСЕв треугольникеАВСс вершинами:А(3,3),В(–1,1),С(0,1).      Решение. Так какЕ– середина отрезкаАВ, то по формуле (4) имеем:.      Длину медианыСЕнайдем по формуле (1):.      Пример. Какие из векторовбудут параллельны и какие перпендикулярны между собой?       Решение. Векторыперпендикулярны, т.к.. Векторыпараллельны, т.к..      Пример. Найти геометрическое место точек, удаленных от точки А(а,b) на одно и тоже расстояниеR.      Решение. Если М(х,у) – произвольная точка искомого геометрического места, то всегда |АМ|=Rили,      (х-а)² + (у-b)²=R²– искомое уравнение.

2. Линии и их уравнения

     Понятия уравнения линии является дальнейшим развитием метода координат. Если точка в аналитической геометрии на плоскости определяется двумя числами (координатами точки), то линия определяется уравнением, связывающим координаты любой точки линии (уравнение линии). Составление уравнения линии заключается в алгебраической записи свойства, характеризующего эту линию как геометрическое место точек.      Точка пересечения двух линий, заданных уравнениями, может быть найдена путем решения системы, образованной из этих уравнений.      На примере уравнения окружности (х–а)²+ (у–b)²=R²видно, что кроме текущих координатхиу, уравнение может содержать еще и некоторые величины, остающиеся неизменными для данной фиксированной линии, но изменяющиеся при переходе к другой линии того же типа. В нашем примере это величиныа,bиR, имеющие для каждой окружности свое значение. Такие величины называются параметрами, они определяют форму и размеры линии (например, параметрRв уравнении окружности), а также положение ее на плоскости относительно системы координат (как, например, координатыаиbцентра окружности).      Пример. Найти уравнение линии, каждая точка которой равноудалена от прямойх= –2 и точки F (2,3).      Решение. Пусть М(х,у) – произвольная точка искомой линии.      Расстояние от точки М до прямойх= –2 есть длина перпендикуляра MN , опущенного из М на прямую. Определим координаты точки N . Очевидно, что абсцисса точки N равна –2, а ордината точки N равна ординате точки М, т.е. N (–2,у). По условию задачи | MN |=| MF |. Следовательно, для любой точки М(х,у), принадлежащей искомой линии, справедливо равенство:

или      .      Упростим полученное уравнение:или.      Это и есть искомое уравнение.

N       y       M(x,y)      F (2,3)                   –2     0        2       x

3. Уравнение прямой линии в пространстве R²: общее, каноническое уравнение прямой. Уравнение прямой с угловым коэффициентом

     В декартовой системе координат прямая представлена уравнением первой степени и, наоборот, всякое уравнение первой степениАх+Ву+С= 0 представляет некоторую прямую. Различные виды уравнения прямой (с угловым коэффициентом, каноническое и т.п.) являются частными случаями этого общего уравнения.      Построим уравнение прямой, проходящей через точкуМ₀(х₀,у₀) параллельно направляющему вектору. Возьмем любую точкуN(х,у), лежащую на заданной прямой. Векторвсегда будет параллелен вектору.      Условие параллельности векторов=(х-х₀;у-у₀) и, дает каноническое уравнение прямой линии на плоскости:.                                                                (1)      Введем вектор, перпендикулярный искомой прямой. Тогда из условия перпендикулярности векторовиможно записать. В результате получаем уравнение:А(х-х₀)+В(у-у₀)=0 илиАх+Ву+С=0,                                                    (2)      где С=–Ах₀–Ву_0.

    Уравнение (2) называется общим уравнением прямой на плоскости. Вектор называется нормалью.      Пример. Написать уравнение прямой, проходящей через точкуQ(2, –3) параллельно оси Оу.

    Решение. В качестве направляющего вектора можно взять вектор. Подставив данные в уравнении (1), получим:. Это каноническое уравнение обычно переписывают в общем виде:х–2=0 илих= 2.      Приобщее уравнение прямой (2) можно переписать в виде:у=k x+b,                                                        (3)      где.      Уравнение (3) называется уравнением с угловым коэффициентом; угловой коэффициентk= tgα, где α – угол наклона прямой к осиОх. Приk=0 ( α= 0)уравнение (3) дает прямую, параллельную осиОх. Из уравнения (3) нельзя получить уравнение прямой, параллельной осиОу. Поэтому все семейство наклонных прямых (3) дополняется прямыми:х=а,(4)       параллельными осиОу. Уравнение (4) получено из уравнения (2) приВ=0, где.Уравнение прямой, проходящей через 2 точки

Пусть даны точки М0(х0, у0) и М1(х1, у1). Требуется написать уравнение прямой, проходящей через эти точки. Для решения задачи воспользуемся уравнением (1). В качестве направляющего вектора воспользуемся вектором:.

      Подставим l=x ₁– x₀иm= y₁–y₀в каноническое уравнение (1), получим уравнение прямой, проходящей через две точки:.                                                              (5)Уравнение прямой, проходящей через данную точку в заданном направленииПусть дана точкаМ₀(х₀, у₀). Требуется написать уравнение прямой, проходящей через точкуМ₀в заданном направлении.      Задачу будем решать в зависимости от того, как определено направление прямой. Если направление задается вектором, то такая прямая описывается уравнением (1). Если задан угловой коэффициентk= k₁, то уравнение прямой будет находить в форме (3):y =k₁ x+ b. Неизвестный коэффициентbнайдем из условияy₀ = k ₁ x₀+ b(точкаМ₀принадлежит прямой). Найденноеb= y₀ – k ₁ x₀подставим в уравнениеy =k₁ x+ b. Искомое уравнение прямой запишем в виде:y– y ₀= k₁( x– x ₀).                                                            (6)      Пример. Написать уравнение прямой, проходящей через точку Q(2,7) параллельно прямой 2х-4у+3=0.      Решение. Найдем угловой коэффициент прямой 2 х–4у+3=0:.      Для искомой прямой угловой коэффициент будет таким же, так как прямые параллельны. Подставим данные в уравнение (6):.

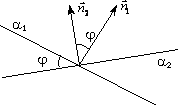
4. Угол между двумя прямыми

Даны уравнения двух прямых. Требуется найти угол между ними. Угол между двумя непараллельными прямыми α1 и α2 найдем как угол между направляющими векторами этих прямых при задании канонических уравнений для α1 и α2, или же как угол между их нормалями, если заданы общие уравнения прямых α1 и α2.

     Пусть заданы две прямые α₁:и α₂:.       Направляющие векторы этих прямых:и.       Угол φ между прямыми найдем из скалярного произведения векторови:.      Пусть заданы общие уравнения прямыхи:А₁х+В₁у+С₁= 0 иА ₂х+В ₂у+С ₂=0. Тогда нормали к этим прямым:и, и.      Если, то изиследует:.      Условием перпендикулярности прямых будет соответственно:либолибо.      Из последнего равенства следует, что. Таким образом угловые коэффициенты двух перпендикулярных прямых обратные по величине и противоположны по знаку.      Условием параллельности прямых будет соответствовать:либолибо.

5. Расстояние от точки до прямой

     Дана прямая Ах+Ву+С=0 и точкаQ(х₁, у₁). Требуется найти расстояние от точкиQдо прямой. Это расстояние находится по формуле:(7)      Пример. Даны вершины треугольникаАВС:А(–2,3),В(1,12),С(11,6). Найти: 1) уравнение стороныАВ; 2) уравнение высотыСD, опущенной из вершиныСна сторонуАВ; 3) уравнение медианыАЕ;  4) уравнение окружности, для которой медианаАЕслужит диаметром.      Решение. 1. Уравнение прямой, проходящей через точкуА(х₁,у₁) иВ(х₂,у₂), имеет вид. Чтобы найти уравнение стороныАВ, подставим координаты точекАиВ в уравнение прямой:;у–3=3х+6;у=3 х+9 (АВ).      2. ВысотаСDперпендикулярна сторонеАВ, а потому их угловые коэффициентыk_CDиk_ABудовлетворяют условию. Из уравнения прямойАВследует, чтоk_AB=3, тогда.      Напишем уравнение прямой, проходящей через данную точку в данном направлении:y – y₁ =k(x– x ₁) . Подставив в уравнение координаты точкиСи угловой коэффициентk_CDполучим искомое уравнение высотыСD:(СD).      3. Определим координаты точкиЕ. Применяем формулы деления отрезка пополам:. Используя координаты вершинВиСполучаем:По точкамАиЕпостроим уравнение медианыАЕ:4. Уравнение окружности радиксаRс центром в точкеК(а,b) имеет вид ( х–а)²+(у–b) ²= R².      Так как по условию медианаАЕявляется диаметром искомой окружности; то центр окружностиКделит отрезокАЕпополам. Находим координаты точкиК:.      Чтобы найти радиусRокружности, достаточно найти расстояние между точкамиАиК. Известно, что расстояниеdмежду двумя точками плоскостиМ₁(х₁,у₁) иМ₂(х₂,у₂) определяется по формуле:. Подставив координаты точекАиК, получаем, т.е.R=5. Следовательно,  (х–2)²+(у–6)²=25 – искомое уравнение окружности.      Пример. В треугольнике с вершинамиА(2,3),В(–1,0),С(4,1) найти длину высоты, опущенной из вершиныАна сторонуВС.      Решение. Составим уравнение прямой, проходящей через сторонуВСпо формуле (5):или.      Найдем длину высотыАЕпо формуле (7):.

12-14 вопрос.

Кривая второго порядка— геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов отличен от нуля.

 ОКРУЖНОСТЬ- замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра). Если R - радиус окружности - расстояние каждой его точки до центра, то длина окружности выразится числом 2pR, а площадь ею ограниченная, числом pR² , где  p=3,14159 - отношение длины окружности к её диаметру.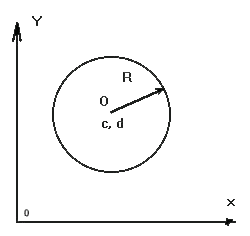

Уравнение окружности в прямоугольной системе координат:

(x-c)² + (y-d)² = R²,

где, c и d - координаты центра.   Отметим, что движение по окружности часто встречается в физике и технике, по круговой траектории движутся люди при катании на колесе обозрения, карусели, по круговым орбитам могут двигаться искусственные спутники Земли. Хорошо известна планетарная модель атома водорода по Резерфорду. В центре атома находится ядро, а электрон вращается вокруг него.

 ЭЛЛИПС(греч. elleipsis - недостаток) - линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающей все прямолинейные образующие одной полости этого конуса.

Эллипс- множество точекМплоскости (рис.1), сумма расстоянийr₁= МF₁иr₂= МF₂которых до двух определенных точекF₁(-c,0)иF₂(c,0)этой плоскости (фокусов эллипса) постоянна

r₁+r₂=2а.

Середина 0 отрезка F₁F₂(фокусного расстояния)называетсяцентром эллипса.

В прямоугольной системе координат 0ху с началом в центре эллипса, на оси0хкоторой лежат фокусы эллипса уравнениеэллипсаимеет следующий вид

х²/а²+у²/в²=1,в²=а²-с²,

где аив- длинны большой и малой полуосей эллипса. При а=в фокусыF₁иF₂совпадают и указанное уравнение определяет окружность, которая рассматривается как частный случай эллипса.

Эллипс- центральнаялиния второго порядка.

Эллипс- замкнутая линия, симметричная относительно осей0xи0yглавных(большойималой)осейи центра.

Форма эллипса (его "вытянутость") определяется значением эксцентриситета e=c/a<1(для окружностие=0)

Прямые D₁D₁'иD₂D₂' (рис.1), параллельные малой оси эллипса и отстоящие от его центра на расстоянииd=±a/e, называются директрисами эллипса, соответствующими фокусамиF₁иF₂. Отношение расстояний любой точки эллипса до фокуса к расстоянию её до соответствующей директрисы постоянно и равно эксцентриситетуr₁/d₁=r₂/d₂=e. Площадь эллипсаS=pi*a*в, pi=3,14159.   Отметим, что по эллипсам движутся планеты вокруг Солнца.

Название "Эллипс" ввёл Аполлоний Пергский, рассматривая эллипс как одно из конических сечений.

ПАРАБОЛА(греч. parabole) – кривая второго порядка.

Прямая пересекает ее не более чем в двух точках . 

При этом парабола может быть определена как:

-множество точек М(xy) плоскости, расстояние FM которых до определенной точки F этой плоскости (фокуса параболы) равно расстоянию MN до определенной прямой АN - директрисы параболы;

-линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и параллельная какой либо касательной плоскости этого конуса ;

-в прямоугольной системе координат 0ху с началом в вершине параболы и осью 0х направленной по оси параболы уравнение параболы имеет так называемый канонический вид

y²=2px,

где р (фокальный параметр) - расстояние от фокуса до директрисы;   Отметим, что по параболе движется тело в однородном поле силы тяжести, брошенное под углом к горизонту, и заряженная частица в однородном электрическом поле плоского конденсатора.

 

 ГИПЕРБОЛА (греч. hyperbole) - плоская кривая линия;

- множество точек М плоскости  разность (по абсолютной величине) расстояний F₁M и F₂M которых до двух определенных точек F₁ и F₂ этой плоскости (фокусов гиперболы) постоянна: F₁M - F₂M=2а<2с

Середина 0 отрезка F₁F₂ (фокусного расстояния) называется центром гиперболы ;

- линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающая обе его полости ;

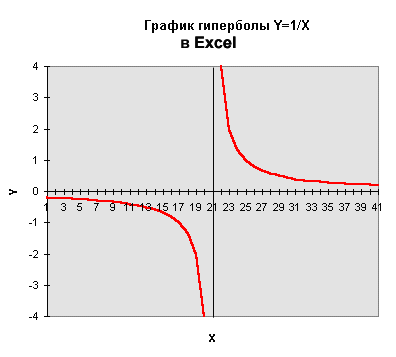
- в прямоугольной системе координат 0ху с началом в центре гиперболы, на оси 0х которой лежат фокусы гиперболы уравнение гиперболы имеет так называемый канонический

х²/а² - у²/в²=1, в²=с² - а²,

где а и в длины полуосей гиперболы .   Отметим, что по гиперболе движутся тела, навсегда покидающие Землю, скорость которых больше, чем 2-я космическая (11,2 км/c). Также по гиперболе движутся альфа-частицы в опыте Резерфорда при рассеивании их ядром атома.