24 Вопрос.

Вертикальная

Вертикальная асимптота — прямая вида при условии существования предела .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

Горизонтальная

Горизонтальная асимптота — прямая вида при условии существования предела

.

Наклонная

Наклонная асимптота — прямая вида при условии существования пределов

Пример наклонной асимптоты

Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!

Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует!

Связь между наклонной и горизонтальной асимптотами

Если при вычислении предела , то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?

Дело в том, что горизонтальная асимптота является частным случаем наклонной при , и из выше указанных замечаний следует, что

• Функция имеет или только одну наклонную асимптоту, или одну горизонтальную асимптоту, или одну наклонную и одну горизонтальную, или две наклонных, или две горизонтальных, либо же вовсе не имеет асимптот.

• Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.

Нахождение асимптот

Порядок нахождения асимптот

Нахождение вертикальных асимптот.

Нахождение двух пределов

Нахождение двух пределов :

если в п. 2.), то, и пределищется по формуле горизонтальной асимптоты,.

Наклонная асимптота — выделение целой части

Также наклонную асимптоту можно найти, выделив целую часть. Например:

Дана функция .

Разделив нацело числитель на знаменатель, получим:

.

При   ,,   то есть:

,

и является искомым уравнением асимптоты.

25 Вопрос.

Схема исследования функции.

7. Найти область определения функции.

8. Проверить, не является ли функция четной или нечетной; проверить также, не является ли она периодической.

9. Найти, если это возможно, точки пересечения графика функции с осями координат и промежутки знакопостоянства функции. Иногда для уточнения построения графика следует найти две три дополнительные точки.

10. Найти производную функции и ее критические точки.

11. Найти промежутки монотонности и экстремумы функции.

12. Построить график функции, используя полученные результаты исследования.

Схема нахождения наибольшего и наименьшего значений функции f(x), непрерывной на отрезке [a; b].

4. Найти значения функции в концах отрезка, т.е. f(a) и f(b) ;

5. Найти значения функции в тех критических точках, которые принадлежат интервалу (a,b) ;

6. Из найденных значений выбрать наибольшее и наименьшее.

26 Вопрос.

Наибольшее и наименьшее значение функции

Постановка задачи. Найти наибольшее и наименьшее значение функции  на отрезке .

План решения. Наибольшее и наименьшее значения непрерывной функции  на данном отрезке  достигаются в критических точках функции (точках, в которых  или не существует) или на концах отрезка .

1. Ищем производную заданной функции.

2. Находим критические точки функции  и выбираем из них те, которые принадлежат данному отрезку .

3. Вычисляем значения функции в критических точках внутри отрезка и значения функции на концах отрезка. Сравнивая полученные значения, находим наибольшее и наименьшее значения функции на отрезке .

Замечание. В текстовых задачах часто бывает найти наименьшее или наибольшее значение некоторой величины. Для этого составляем некоторую функцию, находим ее производную и, исходя из «физического» смысла задачи, выбираем нужное значение переменной, учитывая изменения знаков производной при переходе через критическую точку.

Задача 3. Найти наибольшее и наименьшее значения функций на заданных отрезках.

.

Находим

.

 при ;  не существует при .

 – наименьшее значение функции;

 – наибольшее значение функции;

 – наименьшее значение функции.

Решение многих практических задач часто сводится к нахождению наибольшего и наименьшего значений непрерывной на отрезке функции. В курсах анализа доказывается теорема Вейерштрасса, утверждающая, что непрерывная на отрезке [а; b] функция f принимает на этом отрезке наибольшее и наименьшее значения, т. е. существуют точки отрезка [а; b] в которыхf принимает наибольшее и наименьшее на [а; b] значения.Для случая, когда функция f не только непрерывна на отрезке [а; Ь] но имеет на этом отрезке лишь конечное число критических точек, укажем правило отыскания наибольшего и наименьшего значений f.

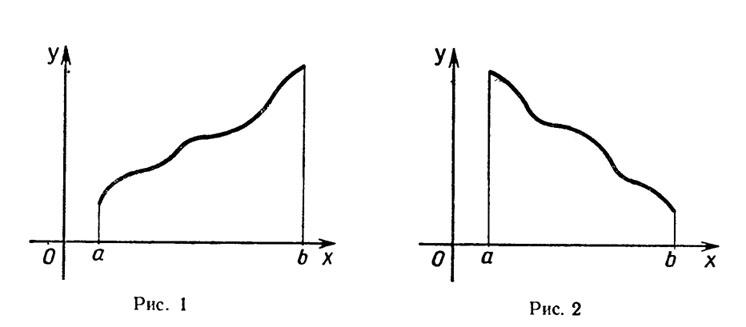
Предположим сначала, что f не имеет на отрезке [а; b] критических точек. Тогда (Критические точки функции) она возрастает (рис. 1) или убывает (рис. 2) на этом отрезке, и, значит, наибольшее и наименьшее значения функции f на отрезке [а; b] — это значения в концах а и b.Пусть теперь функция f имеет на отрезке [а; b] конечное число критических точек. Эти точки разбивают отрезок [а; Ь] на конечное число отрезков, внутри которых критических точек нет. Поэтому наибольшее и наименьшее значения функции f на таких отрезках принимаются в их концах, т. е. в критических точках функции или в точках а и b.Таким образом, чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.Метод поиска наибольших и наименьших значений функции применим к решению разнообразных прикладных задач. При этом действуют по следующей схеме:1) задача «переводится» на язык функций. Для этого выбирают удобный параметр х, через который интересующую нас величину выражают как функцию f (х);2) средствами анализа ищется наибольшее или наименьшее значение этой функции на некотором промежутке;3) выясняется, какой практический смысл (в терминах первоначальной задачи) имеет полученный (на языке функций) результат.Вообще решение практических задач средствами математики, как правило, содержит три основных этапа:1) формализацию (перевод исходной задачи на язык математики);2) решение полученной математической задачи и3) интерпретацию найденного решения («перевод» его с языка математики в терминах первоначальной задачи).С этим общим методом (его называют методом математического моделирования) вы уже знакомы, по описанной схеме решались текстовые задачи в курсе алгебры.