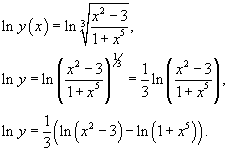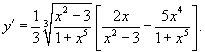20 Вопрос.
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
C' = 0
x' = 1
![]()
![]()
![]()
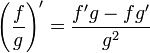 …(g ≠ 0)
…(g ≠ 0)
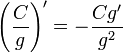 (g ≠ 0)
(g ≠ 0)
Если функция задана параметрический:
![]() ,
то
,
то ![]()
![]()
![]() где
где ![]() — биномиальные
коэффициенты.
— биномиальные
коэффициенты.
Следующие свойства производной служат дополнением к правилам дифференцирования:
если функция дифференцируема на интервале (a,b), то она непрерывна на интервале (a,b). Обратное, вообще говоря, неверно (например, функция y(x) = | x | на [ − 1,1]);
если функция имеет локальный максимум/минимум при значении аргумента, равном x, то f'(x) = 0 (это так называемая лемма Ферма);
производная данной функции единственна, но у разных функций могут быть одинаковые производные.
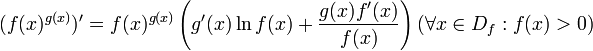
Таблица производных
|
Функция |
Производная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная функции по параметру
Определим
производную функции ![]() по
параметру:
по
параметру:
![]() .
.
Если производная
в точке ![]() существует,
вектор-функция называется дифференцируемой
в этой точке. Координатными функциями
для производной будут
существует,
вектор-функция называется дифференцируемой
в этой точке. Координатными функциями
для производной будут![]() .
.
Свойства производной вектор-функции (всюду предполагается, что производные существуют):
производная суммы есть сумма производных.
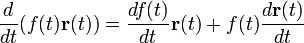 —
здесь
—
здесь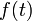
дифференцируемая скалярная функция.
дифференцирование скалярного произведения.
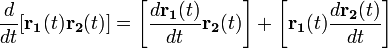 дифференцированиевекторного
произведения.
дифференцированиевекторного
произведения.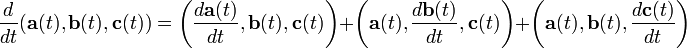 дифференцированиесмешанного
произведения.
дифференцированиесмешанного
произведения.
21 Вопрос.
|
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций. Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей:
Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.
Отсюда видно, что искомая производная равна
|
|
Пример 1 |
|
|
|
Вычислить производную
функции Решение. Применяем логарифмическое дифференцирование: |
|
Пример 2 |
|
|
|
Найти производную
функции Решение. Прологарифмируем обе части и затем продифференцируем. |
|
Пример 3 |
|
|
|
Вычислить производную
функции Решение. Возьмем логарифм от обеих частей: Теперь продифференцируем левую и правую части: |
|
Пример 4 |
|
|
|
Продифференцировать Решение. Сначала возьмем логарифм от обеих частей: Дифференцируя левую и правую части соотношения, получаем Следовательно, производная равна
|

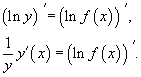
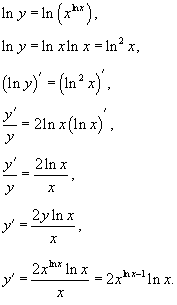
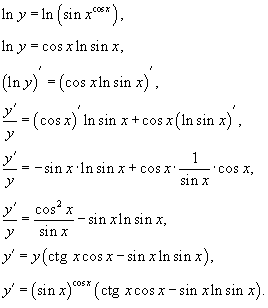
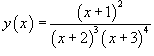 .
.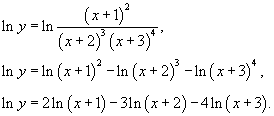
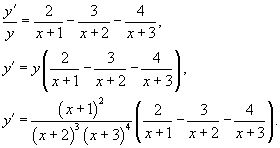
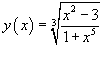 .
.