1 Вопрос.

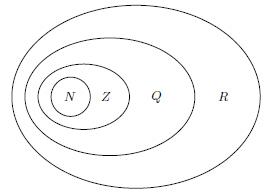
• Числа вида N = {1, 2, 3, ....} называются натуральными. Натуральные числа появились в связи с необходимостью подсчета предметов.

• Числа вида: Z = {... -3, -2, -1, 0, 1, 2, 3, ....} называются целыми числами, т.е. целые числа - это натуральные числа, числа, противоположные натуральным, и число 0.

• Целые и дробные числа составляют множество рациональных чисел: Q = Z {n/m}, где m -целое число, а n -натуральное число.

• Вместе оба множества — рациональных и иррациональных чисел — образуют множество действительных (или вещественных) чисел, которое обозначается R

2 Вопрос.

• Десятичная дробь — это любая числовая дробь, в знаменателе которой стоит степень десятки.

• Существуют знаменатели, которые не приводятся к степени десятки.

• Если в разложении на простые множители присутствуют только множители 2 и 5, это число можно привести к степени десятки. Если найдутся другие числа (3, 7, 11 — что угодно), о степени десятки можно забыть.

• весь алгоритм перехода к десятичным дробям:

1. Разложить знаменатель исходной дроби на множители и убедиться, что она вообще представима в виде десятичной. Т.е. проверить, чтобы в разложении присутствовали только множители 2 и 5. Иначе алгоритм не работает;

2. Сосчитать, сколько двоек и пятерок присутствует в разложении (других чисел там уже не будет, помните?). Подобрать такой дополнительный множитель, чтобы количество двоек и пятерок сравнялось.

3. Собственно, умножить числитель и знаменатель исходной дроби на этот множитель — получим искомое представление, т.е. в знаменателе будет стоять степень десятки.

• Разумеется, дополнительный множитель тоже будет разлагаться только на двойки и пятерки. При этом чтобы не усложнять себе жизнь, следует выбирать наименьший такой множитель из всех возможных.

• если в исходной дроби присутствует целая часть, обязательно переведите эту дробь в неправильную.  И только затем применяйте описанный алгоритм.

• Пример:

Разложим на множители знаменатель первой дроби: 4 = 2 · 2 = 22.Следовательно, дробь представима в виде десятичной. В разложении присутствуют две двойки и ни одной пятерки, поэтому дополнительный множитель равен 52 = 25. С ним количество двоек и пятерок сравняется. Имеем:

Теперь разберемся со второй дробью. Для этого заметим, что24 = 3 · 8 = 3 · 23 — в разложении присутствует тройка, поэтому дробь не представима в виде десятичной.

Две последних дроби имеют знаменатели 5 (простое число)и 20 = 4 · 5 = 22 · 5 соответственно — везде присутствуют только двойки и пятерки. При этом в первом случае «для полного счастья» не хватает множителя 2, а во втором — 5. Получаем:

3 Вопрос.

1.Модуль действительного числа и его свойства.

В младших классах вы уже встречались с понятием модуля (или абсолютной величины) числа, пользовались обозначением | а |. Вы знаете, что, например, | 5 | = 5, | - 3 | = 3. Правда, раньше речь шла только о рациональных числах. Теперь надо  ввести понятие модуля для любого действительного числа.

Определение. Модулем неотрицательного действительного числа х называют само это число: | х | = х; модулем отрицательного действительного числа х называют противоположное число: I х | = - х.  Короче это записывают так:

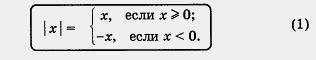Например,

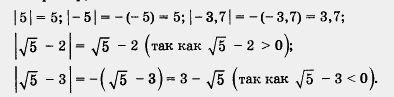На практике используют различные свойства модулей, например:  1. |а|0.  2.|аb| =|a| |b|.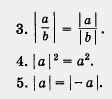2. Геометрический смысл модуля действительного числа

Вернемся к множеству R действительных чисел и его геометрической модели — числовой прямой. Отметим на прямой две точки а и b (два действительных числа а и b), обозначим через (a, b) расстояние между точками а и b (— буква греческого алфавита «ро»). Это расстояние равно b - а, если  b > а (рис. 101), оно равно а - b, если а > b (рис. 102), наконец, оно равно нулю, если а = b.

Все три случая охватываются одной формулой: 

Пример 1. Решить уравнения:  а) | х - 2| = 3; б) | х + 3,2| = 2; в) | х | = 2,7; г) | x - I = 0.  Решение, а) Переведем аналитическую модель |х - 2| = 3 на геометрический язык: нам нужно найти на координатной прямой такие точки х, которые удовлетворяют условию(х, 2) = 3, т. е. удалены от точки 2 на расстояние, равное 3. Это — точки - 1 и 5 (рис. 103). Следовательно, уравнение имеет  два корня: - 1 и 5.

б) Уравнение | х + 3,2 | = 2 перепишем в виде | х - (— 3,2) | = 2 и далее (х, - 3,2) = 2. На координатной прямой есть две точки, которые удалены от точки - 3,2 на расстояние, равное 2. Это — точки - 5,2 и - 1,2 (рис. 104). Значит, уравнение имеет два корня: -5,2 и - 1,2.

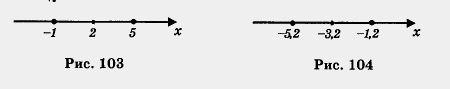в) Уравнение |x| = 2,7 перепишем в виде |х - 0| = 2,7, или, что то же самое, (х, 0) = 2,7. На координатной прямой имеются две точки, которые удалены от точки О на расстояние, равное 2,7. Это — точки - 2,7 и 2,7 (рис. 105). Таким образом, уравнение имеет два корня: - 2,7 и 2,7'.  г) Для уравнения

|х - | = 0 можно обойтись без геометрическои иллюстрации, ведь если | а | = 0, то а = 0. Поэтому х -= 0, т. е. х =.

Пример 2. Решить уравнения:  а) |2х - 6| = 8; б) |5 - Зx | = 6; в) |4x + 1| = - 2.

Р е ш е н и е. а) Имеем

|2x - 6| = |2(x -3)| =|2|.| = 2|x -3| Значит, заданное уравнение можно преобразовать к виду  2|х - 3| = 8, откуда получаем | х - 3| = 4.  Переведем аналитическую модель | х - 3 | = 4 на геометрический язык:

нам нужно найти на координатной прямой такие точки х, которые удовлетворяют условию (х, 3) = 4, т.е. удалены от точки 3 на расстояние, равное 4. Это — точки - 1 и 7  (рис. 106). Итак, уравнение имеет два корня: - 1 и 7.  б) Имеем

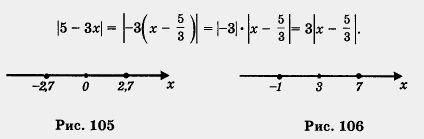Поэтому заданное уравнение можно преобразовать к виду

Переведем аналитическую модель на геометрический язык: нам нужно найти на координатной прямой такие точки х, которые удовлетворяют условию

Значит, они удалены от точки , на расстояние, равное 2.

в) Для уравнения  | 4х + 1 | = - 2 никаких преобразований делать не нужно. Оно явно не имеет корней, поскольку в левой его части содержится неотрицательное выражение, а в правой — отрицательное число.

Пример 3. Построить график функции у = |х + 2 |.

Решение. График этой функции получается из графика функции у = | х | сдвигом последнего на две единицы масштаба влево (рис. 111).

4. Тождество Мы знаем, что если.А как быть, если а < 0? Написать ув этом случае нельзя, ведь а < 0 и получится, что, а это неверно, так как значение квадратного корня не может быть отрицательным.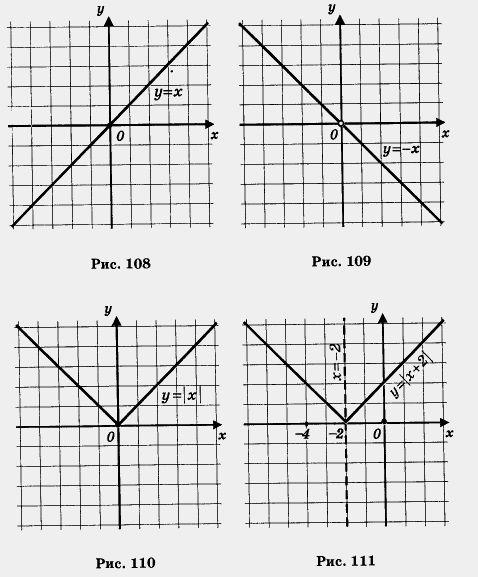

Чему же равно выражениепри а < 0? По определению квадратного корня в ответе должно получиться такое число, которое, во-первых, положительно и, во-вторых, при возведении в квадрат дает подкоренное число, т. е. а². Таким числом будет - а. Смотрите: 1) - а > 0 (еще раз напомним, что а — отрицательное число, значит, - а — положительное число);  2)(-а)²=а².  Итак,

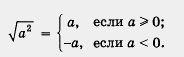Вам ничего не напоминает конструкция, полученная в правой части равенства? Вспомните, ведь точно так же определяется модуль числа а:

Значит,и | а | — одно и то же. Тем самым мы доказали важное тождество:

В роли а может выступать любое числовое или алгебраическое выражение.

Пример 4. Упростить выражение , если:  а) а - 1 > 0; б) а - 1 < 0.  Решение. Как мы только что установили, справедливо тождество

а) Если а - 1 > 0, то | а - 1| = а - 1. Таким образом, в этом случае получаем = а - 1.  б) Если а - 1 <0, то |а - 1| = -(а - 1) = 1 - а. Значит, в этом случае получаем= 1 - а. в