2. Линейные операции с векторами Сложение векторов

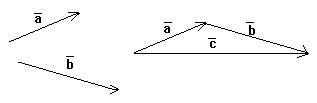
1. Правилом треугольника Суммой двух векторов иназывается третий вектор, соединяющий начало векторас концом вектора, при условии, что начало векторапомещено в конец вектора.

2 Правило параллелограмм. Если векторы ипривести к общему началу и построить на векторахипараллелограмм, то диагональ параллелограмма, выходящая из общего начала, называется суммой векторови.

3 Правило многоугольника. Если векторы расположить так, чтобы начало каждого следующего вектора поместить в конец предыдущего, то суммой нескольких векторов называется вектор, соединяющий начало самого первого вектора с концом последнего

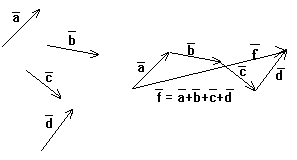
Число слагаемых векторов может быть любое конечное, многоугольник в результате сложения может быть выпуклым, а может и нет .

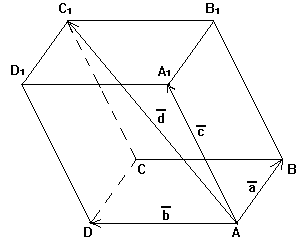
4.Правило параллелепипеда. Сумма трех некомпланарных векторов, приведенных к общему началу, равна диагонали параллелепипеда, построенного на этих векторах, выходящая из общего начала.

.

Если обозначить , тогда получим:

Вычитание

Правило 5 Разностью двух векторов иназывается третий вектор,который в сумме с векторомдаёт вектор.

т.е. .

Если привести векторы к общему началу и построить на них параллелограмм, то диагональ параллелограмма, не выходящая из общего начала, является разностью векторов, т.е. разность векторов – вектор, проведённый из конца вычитаемого в конец уменьшаемого.

Свойства (суммы и разности векторов)

Относительно сложения имеют место законы:

1) - коммутативный (переместительный);

2) - ассоциативный (сочетательный);

3) для любого вектора существует нулевой вектор, такой,

что;

4) для каждого вектора существует вектор такой, чтовекторназывается противоположным векторуи обозначается, т.е.=-.

Умножение вектора на число

Правило 6.Произведением вектора на числоназывается вектор, коллинеарный вектору, длина которого равна, а направление совпадает с вектором, если, и противоположное, если.

.

Относительно умножения на число имеют место законы:

а) -распределительный;

б) -сочетательный ;

в) -коммутативный.

3. Проекция вектора на ось

Пусть в пространстве задана ось l.

Опр.10 Проекцией точки М на ось l называется основание М₁

перпендикуляра ММ₁, опущенного из точки на ось.

Опр.11.Проекцией вектора на ось l называется длина отрезка, взятая со знаком «+», если направление его совпадает с направлением оси и со знаком «-», если направлениепротивоположно направлению оси.

Обозначается .

Проекция вектора на ось равна произведению его модуля на косинус угла , который вектор образует с осью.

При этом углом между вектором и осью называется угол, на который нужно повернуть ось до совмещения с вектором против хода часовой стрелки.

4.Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы

Проекции вектора на оси координат называются его координатами. В этом заключается их геометрический смысл.

Если задана система координат на плоскости и в пространстве, то начало вектора можно всегда совместить с началом координат, не меняя при этом длину и направление. Выделим на координатных осях единичные векторы и обозначим .Выберем произвольный вектор. Найдем проекции вектора на координатные оси.

Проведем через конец вектора плоскости, параллельные координатным плоскостям. Точки пересечения с осями обозначим соответственно через М₁,М₂,М₃. Получили прямоугольный параллелепипед, одной диагональю которого является .

Тогда ;;

. По определению суммы получим, что , но т.к.,то

.

Но ,,